5.1.1 相交线课件
图片预览








文档简介
课件27张PPT。第5章 相交线与平行线5.1 相交线第1课时 相交线1课堂讲解邻补角
对顶角及其性质2课时流程逐点
导讲练课堂小结作业提升 如图所示,图中的道路是有宽度的,是有限长的,
而且也不是完全直的,当我们把它们看成直线时,这
些直线有些是相交线,有些是平行线.相交线、平行
线都有许多重要性质,并且在生产和生活中有广泛应
用.所以研究这些问题对今后的工作和学习都是有用
的,也将为后面的
学习做些准备.我
们先研究直线相交
的问题.1知识点邻补角 如图,观察剪刀剪开布片过程中有关角的变化.可
以发现,握紧剪刀的把手时,随着两 个把手之间的角
逐渐变小,剪刀刃之间的角也相应变小,直到剪开布
片.如果把剪刀的构造看作 两条相
交的直线,这就关系到两条相交
直线所成 的角的问题.知1-导知1-导探究
任意画两条相交的直线,形成四个角 (如图), ∠1
与∠2有怎样的位置关系?
分别量一下各个角的度数, ∠1与∠2的度 数有什
么关系?在上页图中剪刀把手之间的角变化的过程中,
这个关系还保持吗?
为什么?知1-导 ∠1与∠2有一条公共边OC,它们的另一边互为
反向延长线(∠1与∠2互补), 具有这种关系的两个角,
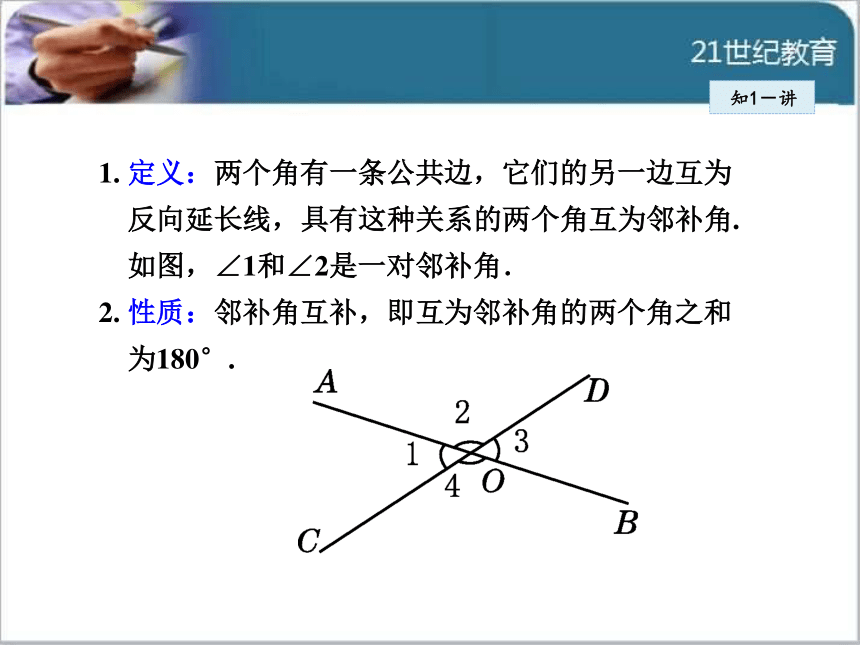
互为邻补角)adjacent angles on a straight line).知1-讲1. 定义:两个角有一条公共边,它们的另一边互为
反向延长线,具有这种关系的两个角互为邻补角.
如图,∠1和∠2是一对邻补角.
2. 性质:邻补角互补,即互为邻补角的两个角之和
为180°.知1-讲要点精析:
(1)邻补角是成对出现的,而且互为邻补角,单独一个
角不能成为邻补角;
(2)邻补角是集数形结合为一体的概念之一,它既指明
了位置关系,又包含了数量关系;“邻”指位置相
邻;“补”指两个角之和为180°.
(3)互为邻补角的“两要素”:
①有一条边是公共边;
②另一边互为反向延长线.知1-讲如图所示,直线AB,CD,
EF相交于点O,指出∠AOC,
∠EOB的邻补角.例1找一个角的邻补角时,可先固定一边,反向延长另一边,
则由固定的一边和另一边的反向延长线组成的角即是原角
的邻补角.∠AOC的邻补角有两个:固定射线OA,反向
延长射线OC得到∠AOD;固定射线OC,反向延长射线
OA得到∠BOC,它们都是∠AOC的邻补角.同理,
∠EOB的邻补角也有两个,为∠BOF和∠AOE.
∠AOC的邻补角是∠AOD,∠BOC;∠EOB的邻补角是
∠BOF和∠AOE.导引:解:知1-讲判断两个角是不是邻补角,应从两个方面去看:
一看这两个角有没有公共边;
二看这两个角的另一边是否互为反向延长线.知1-练1 邻补角是( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且和为180°的两个角
D.有公共顶点且有一条公共边,另一边互为
反向延长线的两个角
识别邻补角应同时满足以下三条:
①有公共______;②有一条公共边;
③两角的另一边______________.知1-练3 下列选项中,∠1与∠2互为邻补角的是( )4 如图,∠1的邻补角是( )
A.∠BOC
B.∠BOE和∠AOF
C.∠AOF
D.∠BOC和∠AOF知1-练2知识点对顶角及其性质知2-导探究
任意画两条相交的直线,形成四个角 (如图), ∠1
与∠3有怎样的位置关系?
分别量一下各个角的度数, ∠1与∠3的度 数有什
么关系?在知1图中剪刀
把手之间的角变化的过程
中,这个关系还保持吗?
为什么?知2-导问题:学生根据观察和度量完成下表:知2-导 ∠1与∠3有一个公共顶点O,并且∠1的两边分别是
∠3的两边的反向延长线,具有这种位置 关系的两个角,
互为对顶角(opposite angles).
在上图中, ∠1与∠2互补, ∠3与∠2互 补,由
“同角的补角相等”,可以得出∠1=∠3.类似 地,
∠2=∠4.
这样,我们得到对顶角的性质:对顶角相等.?知2-讲定义:两个角有一个公共的顶点,并且一个角的
两边分别是另一个角的两边的反向延长线,具有
这种位置关系的两个角,互为对顶角.如图,
∠1和∠3是对顶角.
2.性质:对顶角相等.知2-讲要点精析:
(1)对顶角都是成对出现的,当两个角互为对顶角时,
其中一个角叫做另一个角的对顶角;
(2)对顶角的两边互为反向延长线即在同一直线上,
其实质是:对顶角是两直线相交所成的没有公共
边的两个角;
(3)对顶角的条件:
①有公共顶点;②两边互为反向延长线.知2-讲〈铜仁〉如图,∠1与∠2是对顶角的是( )例2判断两个角是不是对顶角,要紧扣对顶角的定义,
A图中∠1和∠2的顶点不同;B图中∠1和∠2的两
边都不是互为反向延长线;C图中的∠1和∠2符合
定义;D图中∠1和∠2有一条公共边.导引:C知2-讲判断两个角是否互为对顶角的方法:
一看它们有没有公共顶点;
二看这两个角的两边是否互为反向延长线,实质就
是看这两个角是否是两条直线相交所成的没有公共
边的两个角.知2-讲如图,直线a, b相交,∠1 = 40°, 求∠2, ∠3, ∠4的度数.
由邻补角的定义,得
∠2 = 180°-∠1
= 180°-40°=140°;
由对顶角相等,得
∠3= ∠1=40° ,
∠4= ∠2 = 140°.例3解:知2-讲 对顶角和邻补角经常在求角的度数的题目中同
时用到,只要分清楚对顶角、邻补角的性质,就是
对顶角相等、邻补角互补,此类题目容易解答.知2-练如图,取两根木条a,b,将它们钉在一起,并把它
们想象成两条直线,就得到一个相交线的模型.你
能说出其中的一些邻补角与对顶角吗?两根木条
所成的角中,如果∠α=35°,其他三 个角各等于
多少度?如果∠α等于90°,115°,m°呢如图,小强和小丽一起玩跷跷板,横板AB绕O
上下转动,当小强从A到A′的位置时,
∠AOA′=45°,则∠BOB′的度数为________,
理由是___________________________________
_________________________________________.知2-练如图,直线AB,CD相交于点O,则∠1______
∠2,根据的是____________;∠2+∠3=
________,根据的是________________.知2-练如图,直线AB,CD交于点O,下列说法中,错
误的是( )
A.∠AOC与∠BOD是对顶角
B.∠AOE与∠BOE是邻补角
C.∠DOE与∠BOC是对顶角
D.∠AOD与∠BOC都是∠AOC的邻补角知2-练
对顶角及其性质2课时流程逐点
导讲练课堂小结作业提升 如图所示,图中的道路是有宽度的,是有限长的,
而且也不是完全直的,当我们把它们看成直线时,这
些直线有些是相交线,有些是平行线.相交线、平行
线都有许多重要性质,并且在生产和生活中有广泛应
用.所以研究这些问题对今后的工作和学习都是有用
的,也将为后面的
学习做些准备.我
们先研究直线相交
的问题.1知识点邻补角 如图,观察剪刀剪开布片过程中有关角的变化.可
以发现,握紧剪刀的把手时,随着两 个把手之间的角
逐渐变小,剪刀刃之间的角也相应变小,直到剪开布
片.如果把剪刀的构造看作 两条相
交的直线,这就关系到两条相交
直线所成 的角的问题.知1-导知1-导探究
任意画两条相交的直线,形成四个角 (如图), ∠1
与∠2有怎样的位置关系?
分别量一下各个角的度数, ∠1与∠2的度 数有什
么关系?在上页图中剪刀把手之间的角变化的过程中,
这个关系还保持吗?
为什么?知1-导 ∠1与∠2有一条公共边OC,它们的另一边互为
反向延长线(∠1与∠2互补), 具有这种关系的两个角,
互为邻补角)adjacent angles on a straight line).知1-讲1. 定义:两个角有一条公共边,它们的另一边互为
反向延长线,具有这种关系的两个角互为邻补角.
如图,∠1和∠2是一对邻补角.
2. 性质:邻补角互补,即互为邻补角的两个角之和
为180°.知1-讲要点精析:
(1)邻补角是成对出现的,而且互为邻补角,单独一个
角不能成为邻补角;
(2)邻补角是集数形结合为一体的概念之一,它既指明
了位置关系,又包含了数量关系;“邻”指位置相
邻;“补”指两个角之和为180°.
(3)互为邻补角的“两要素”:
①有一条边是公共边;
②另一边互为反向延长线.知1-讲如图所示,直线AB,CD,
EF相交于点O,指出∠AOC,
∠EOB的邻补角.例1找一个角的邻补角时,可先固定一边,反向延长另一边,
则由固定的一边和另一边的反向延长线组成的角即是原角
的邻补角.∠AOC的邻补角有两个:固定射线OA,反向
延长射线OC得到∠AOD;固定射线OC,反向延长射线
OA得到∠BOC,它们都是∠AOC的邻补角.同理,
∠EOB的邻补角也有两个,为∠BOF和∠AOE.
∠AOC的邻补角是∠AOD,∠BOC;∠EOB的邻补角是
∠BOF和∠AOE.导引:解:知1-讲判断两个角是不是邻补角,应从两个方面去看:
一看这两个角有没有公共边;
二看这两个角的另一边是否互为反向延长线.知1-练1 邻补角是( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且和为180°的两个角
D.有公共顶点且有一条公共边,另一边互为
反向延长线的两个角
识别邻补角应同时满足以下三条:
①有公共______;②有一条公共边;
③两角的另一边______________.知1-练3 下列选项中,∠1与∠2互为邻补角的是( )4 如图,∠1的邻补角是( )
A.∠BOC
B.∠BOE和∠AOF
C.∠AOF
D.∠BOC和∠AOF知1-练2知识点对顶角及其性质知2-导探究
任意画两条相交的直线,形成四个角 (如图), ∠1
与∠3有怎样的位置关系?
分别量一下各个角的度数, ∠1与∠3的度 数有什
么关系?在知1图中剪刀
把手之间的角变化的过程
中,这个关系还保持吗?
为什么?知2-导问题:学生根据观察和度量完成下表:知2-导 ∠1与∠3有一个公共顶点O,并且∠1的两边分别是
∠3的两边的反向延长线,具有这种位置 关系的两个角,
互为对顶角(opposite angles).
在上图中, ∠1与∠2互补, ∠3与∠2互 补,由
“同角的补角相等”,可以得出∠1=∠3.类似 地,
∠2=∠4.
这样,我们得到对顶角的性质:对顶角相等.?知2-讲定义:两个角有一个公共的顶点,并且一个角的
两边分别是另一个角的两边的反向延长线,具有
这种位置关系的两个角,互为对顶角.如图,
∠1和∠3是对顶角.
2.性质:对顶角相等.知2-讲要点精析:
(1)对顶角都是成对出现的,当两个角互为对顶角时,
其中一个角叫做另一个角的对顶角;
(2)对顶角的两边互为反向延长线即在同一直线上,
其实质是:对顶角是两直线相交所成的没有公共
边的两个角;
(3)对顶角的条件:
①有公共顶点;②两边互为反向延长线.知2-讲〈铜仁〉如图,∠1与∠2是对顶角的是( )例2判断两个角是不是对顶角,要紧扣对顶角的定义,
A图中∠1和∠2的顶点不同;B图中∠1和∠2的两
边都不是互为反向延长线;C图中的∠1和∠2符合
定义;D图中∠1和∠2有一条公共边.导引:C知2-讲判断两个角是否互为对顶角的方法:
一看它们有没有公共顶点;
二看这两个角的两边是否互为反向延长线,实质就
是看这两个角是否是两条直线相交所成的没有公共
边的两个角.知2-讲如图,直线a, b相交,∠1 = 40°, 求∠2, ∠3, ∠4的度数.
由邻补角的定义,得
∠2 = 180°-∠1
= 180°-40°=140°;
由对顶角相等,得
∠3= ∠1=40° ,
∠4= ∠2 = 140°.例3解:知2-讲 对顶角和邻补角经常在求角的度数的题目中同
时用到,只要分清楚对顶角、邻补角的性质,就是
对顶角相等、邻补角互补,此类题目容易解答.知2-练如图,取两根木条a,b,将它们钉在一起,并把它
们想象成两条直线,就得到一个相交线的模型.你
能说出其中的一些邻补角与对顶角吗?两根木条
所成的角中,如果∠α=35°,其他三 个角各等于
多少度?如果∠α等于90°,115°,m°呢如图,小强和小丽一起玩跷跷板,横板AB绕O
上下转动,当小强从A到A′的位置时,
∠AOA′=45°,则∠BOB′的度数为________,
理由是___________________________________
_________________________________________.知2-练如图,直线AB,CD相交于点O,则∠1______
∠2,根据的是____________;∠2+∠3=
________,根据的是________________.知2-练如图,直线AB,CD交于点O,下列说法中,错
误的是( )
A.∠AOC与∠BOD是对顶角
B.∠AOE与∠BOE是邻补角
C.∠DOE与∠BOC是对顶角
D.∠AOD与∠BOC都是∠AOC的邻补角知2-练
