5.1.3 垂线段课件
图片预览










文档简介
课件30张PPT。第5章 相交线与平行线5.1 相交线第3课时 垂线段1课堂讲解垂线段的定义
垂线段的性质
点到直线的距离2课时流程逐点
导讲练课堂小结作业提升 如图所示, 村庄A要从河流 l 引水入庄, 需修筑一
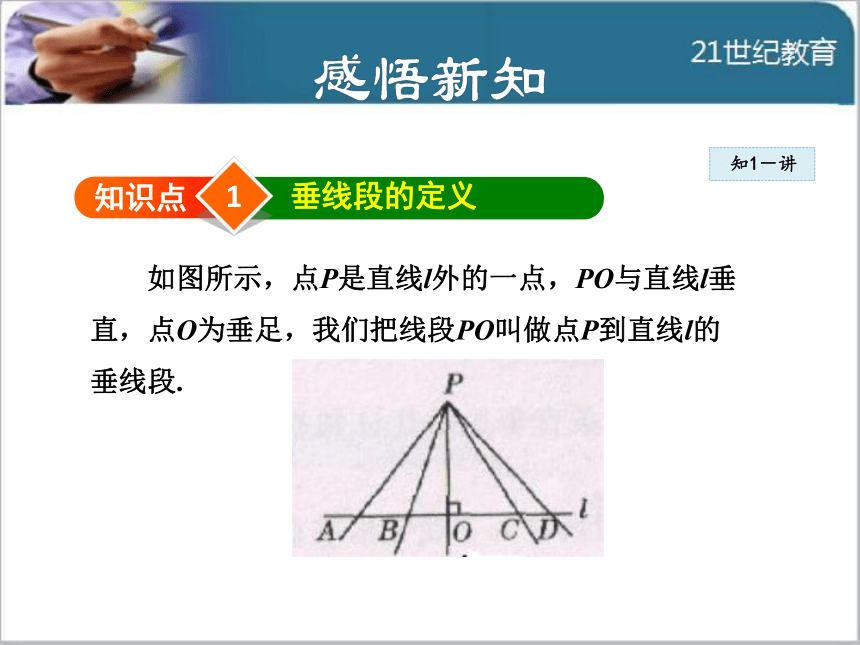
水渠, 如何修水渠最短呢?1知识点垂线段的定义 如图所示,点P是直线l外的一点,PO与直线l垂
直,点O为垂足,我们把线段PO叫做点P到直线l的
垂线段.知1-讲知1-讲 过直线外一点画已知直线的垂线,连接这点
与垂足之间的线段,叫做这点到已知直线的垂线
段.知1-讲如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AB;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到BC的距离.
A.2 B.3
C.4 D.5例1A知1-讲根据垂直定义,可知①正确,②错误;点C到AB
的垂线段应是线段AC,故③错误;点到直线的距
离是线段的长度而不是线段,故④⑥错误;⑤符
合定义,正确. 分析: 知1-讲 解答概念、性质辨析题,首先要熟记概念和性
质,然后根据垂线的定义与性质、垂线段与点到直线
距离的概念作出正确的判断即可.所以记忆与理解相
结合是学好数学的前提.知1-练1 下列说法正确的是( )
A.垂线段就是垂直于已知直线的线段
B.垂线段就是垂直于已知直线并且与已知直线相
交的线段
C.垂线段是一条竖起来的线段
D.过直线外一点向该直线作垂线,这一点到垂足
之间的线段叫垂线段
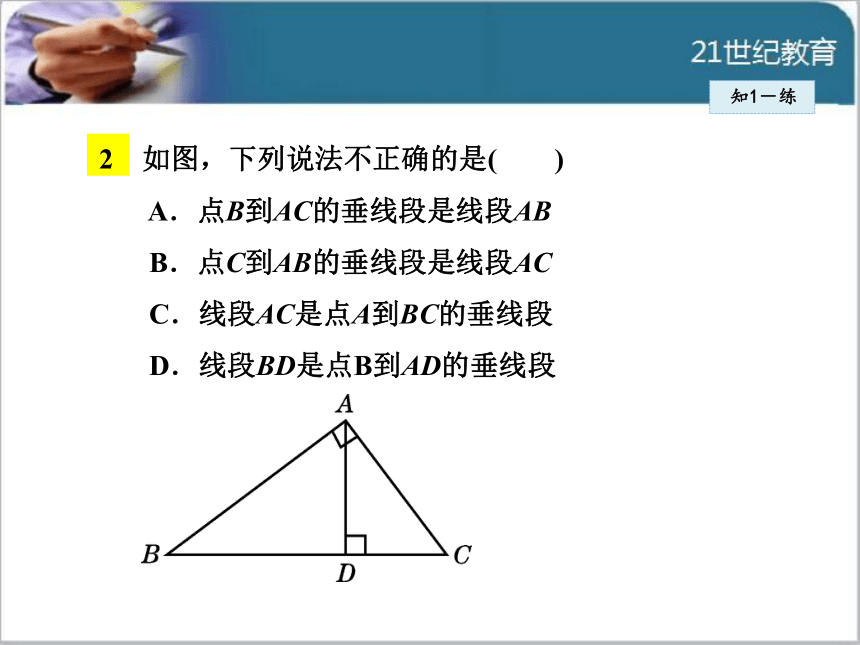
2 如图,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB
B.点C到AB的垂线段是线段AC
C.线段AC是点A到BC的垂线段
D.线段BD是点B到AD的垂线段 知1-练2知识点垂线段的性质知2-导思考
如图,在灌溉时,要把河中的水引到农田P处,
如何挖渠能使渠道最短?知2-导探究
如图,连接直线l外一点P与直线 l上各点O, A1, A2,
A3, …,其中PO⊥l (我们称PO为点P到直线l的垂线段).
比较线段 PO, PA1,PA2, PA3,…的长短,这些线段中,
哪一条最短?知2-导 连接直线外一点与直线上各点的所有线段中,
垂线段最短.
简单说成:垂线段最短.知2-讲如图所示,AB是一条河流,要铺设管道将河水引
到C、D两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D作AB的垂线,垂足分别为点E,F,沿CE,DF铺设管道;
方案二:连接CD交AB于点P,
沿PC,PD铺设管道.
这两种铺设管道的方案哪一种
更节省材料?为什么?
(忽略河流的宽度)例2知2-讲要尽可能节省材料,也就是让管道的总长度最
短.方案一中CE,DF是垂线段,而方案二中PC,
PD不是垂线段,所以CE<PC,DF<PD,所以
CE+DF<PC+PD,所以方案一更节省材料.解:导引:按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,CD不垂直于AB,
根据“垂线段最短”可知,CE<PC,DF<DP,
所以CE+DF<PC+DP.
所以沿CE,DF铺设管道更节省材料.知2-讲 本题主要利用“垂线段最短”来解决实际问题,
解这类求最短距离问题时,要注意“垂线段最短”与
“两点之间,线段最短”的区别,辨明这两条性质的应
用条件:点到直线的距离,两点间的距离;正确运用
解题方法.知2-讲 例3 如图,平原上有A,B,C,D四个村庄,为解
决当地缺水问题,政府准备投资修建一个蓄水
池.
(1)不考虑其他因素,请你画图确定蓄水池H的位
置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?
并说明根据.
知2-讲解:(1)如图,连接AD,BC,交于点H,则H点为蓄水池
的位置,它到四个村庄距离之和最小.
(2)如图,过点H作HG⊥EF,垂足为G,则沿HG开
渠最短.根据:连接直线外一点与直线上各点的
所有线段中,垂线段最短.知2-讲 本题考查了垂线段的性质在实际生活中的运用.
体现了建模思想的运用. 1 如图,计划在河边建一水厂,过C点作CD⊥AB于D
点.在D点建水厂,可使水厂到村庄C的路程最短,
这样设计的依据是____________________.知2-练如图,AD⊥BD,BC⊥CD,AB=6 cm,BC=4 cm,
则BD的长度的取值范围是( )
A.大于4 cm
B.小于6 cm
C.大于4 cm或小于 6 cm
D.大于 4 cm且小于 6 cm知2-练 3 如图,三角形ABC中,∠C=90°,AC=3,点P
可以在直线BC上自由移动,则AP的长不可能是
( )
A.2.5 B.3 C.4 D.5知2-练3知识点点到直线的距离知3-讲 点到直线的距离:从直线外一点到这条直线的垂
线段的长度,叫做点到直线的距离.
(1)因为某点到已知直线的垂线段只有一条,所以点到
直线的距离是唯一的;
(2)当这个点在已知直线上时,可看作点到直线的距离
为0;知3-讲 例4 如图,在三角形ABC中,∠ACB=90°,CD⊥
AB,垂足为D.若AC=4 cm,BC=3 cm,AB=
5 cm,则点A到直线BC的距离为______cm,点
B到直线AC的距离为______cm,点C到直线AB
的距离为______cm.432.4知3-讲导引:根据点到直线的距离的定义可知,点A到直线BC
的距离是线段AC的长,点B到直线AC的距离是线
段BC的长,点C到直线AB的距离是线段CD的长.
因为三角形ABC的面积S=
所以AC·BC=AB·CD,进而可得CD=2.4 cm.知3-讲 正确理解点到直线的距离及两点间的距离是解决
此类问题的关键.解决此类问题应注意:(1)点到直线
的距离是点到直线的垂线段的长度,而不是垂线,也
不是垂线段;(2)距离表示线段的长度,是一个数量,
与线段不能等同;(3)用垂线段的长度表示点到直线的
距离,其实质是点与垂足两点间的距离,体现了数形
结合思想.如图所示的是小凡同学在体育课上跳远后留下的
脚印,他的跳远成绩是线段________的长度.知3-练如图,其长能表示点到直线(线段)的距离的线段
的条数是( )
A.3
B.4
C.5
D.6知3-练3 点到直线的距离是指( )
A.直线外一点到这条直线的垂线的长度
B.直线外一点到这条直线上的任意一点的距离
C.直线外一点到这条直线的垂线段
D.直线外一点到这条直线的垂线段的长度知3-练
1. 垂线、垂直与垂线段的关系:
(1)区别:垂线是一条与已知直线垂直的直线;垂直
是两条直线之间的位置关系;垂线段是一条与已
知直线垂直的线段.
(2)联系:垂线段所在的直线是已知直线的垂线;垂
线段所在的直线与已知直线垂直.
2. 点到直线的距离:直线外一点到这条直线的垂线段
的长度,叫做点到直线的距离.
垂线段的性质
点到直线的距离2课时流程逐点
导讲练课堂小结作业提升 如图所示, 村庄A要从河流 l 引水入庄, 需修筑一
水渠, 如何修水渠最短呢?1知识点垂线段的定义 如图所示,点P是直线l外的一点,PO与直线l垂
直,点O为垂足,我们把线段PO叫做点P到直线l的
垂线段.知1-讲知1-讲 过直线外一点画已知直线的垂线,连接这点
与垂足之间的线段,叫做这点到已知直线的垂线
段.知1-讲如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AB;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到BC的距离.
A.2 B.3
C.4 D.5例1A知1-讲根据垂直定义,可知①正确,②错误;点C到AB
的垂线段应是线段AC,故③错误;点到直线的距
离是线段的长度而不是线段,故④⑥错误;⑤符
合定义,正确. 分析: 知1-讲 解答概念、性质辨析题,首先要熟记概念和性
质,然后根据垂线的定义与性质、垂线段与点到直线
距离的概念作出正确的判断即可.所以记忆与理解相
结合是学好数学的前提.知1-练1 下列说法正确的是( )
A.垂线段就是垂直于已知直线的线段
B.垂线段就是垂直于已知直线并且与已知直线相
交的线段
C.垂线段是一条竖起来的线段
D.过直线外一点向该直线作垂线,这一点到垂足
之间的线段叫垂线段
2 如图,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB
B.点C到AB的垂线段是线段AC
C.线段AC是点A到BC的垂线段
D.线段BD是点B到AD的垂线段 知1-练2知识点垂线段的性质知2-导思考
如图,在灌溉时,要把河中的水引到农田P处,
如何挖渠能使渠道最短?知2-导探究
如图,连接直线l外一点P与直线 l上各点O, A1, A2,
A3, …,其中PO⊥l (我们称PO为点P到直线l的垂线段).
比较线段 PO, PA1,PA2, PA3,…的长短,这些线段中,
哪一条最短?知2-导 连接直线外一点与直线上各点的所有线段中,
垂线段最短.
简单说成:垂线段最短.知2-讲如图所示,AB是一条河流,要铺设管道将河水引
到C、D两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D作AB的垂线,垂足分别为点E,F,沿CE,DF铺设管道;
方案二:连接CD交AB于点P,
沿PC,PD铺设管道.
这两种铺设管道的方案哪一种
更节省材料?为什么?
(忽略河流的宽度)例2知2-讲要尽可能节省材料,也就是让管道的总长度最
短.方案一中CE,DF是垂线段,而方案二中PC,
PD不是垂线段,所以CE<PC,DF<PD,所以
CE+DF<PC+PD,所以方案一更节省材料.解:导引:按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,CD不垂直于AB,
根据“垂线段最短”可知,CE<PC,DF<DP,
所以CE+DF<PC+DP.
所以沿CE,DF铺设管道更节省材料.知2-讲 本题主要利用“垂线段最短”来解决实际问题,
解这类求最短距离问题时,要注意“垂线段最短”与
“两点之间,线段最短”的区别,辨明这两条性质的应
用条件:点到直线的距离,两点间的距离;正确运用
解题方法.知2-讲 例3 如图,平原上有A,B,C,D四个村庄,为解
决当地缺水问题,政府准备投资修建一个蓄水
池.
(1)不考虑其他因素,请你画图确定蓄水池H的位
置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?
并说明根据.
知2-讲解:(1)如图,连接AD,BC,交于点H,则H点为蓄水池
的位置,它到四个村庄距离之和最小.
(2)如图,过点H作HG⊥EF,垂足为G,则沿HG开
渠最短.根据:连接直线外一点与直线上各点的
所有线段中,垂线段最短.知2-讲 本题考查了垂线段的性质在实际生活中的运用.
体现了建模思想的运用. 1 如图,计划在河边建一水厂,过C点作CD⊥AB于D
点.在D点建水厂,可使水厂到村庄C的路程最短,
这样设计的依据是____________________.知2-练如图,AD⊥BD,BC⊥CD,AB=6 cm,BC=4 cm,
则BD的长度的取值范围是( )
A.大于4 cm
B.小于6 cm
C.大于4 cm或小于 6 cm
D.大于 4 cm且小于 6 cm知2-练 3 如图,三角形ABC中,∠C=90°,AC=3,点P
可以在直线BC上自由移动,则AP的长不可能是
( )
A.2.5 B.3 C.4 D.5知2-练3知识点点到直线的距离知3-讲 点到直线的距离:从直线外一点到这条直线的垂
线段的长度,叫做点到直线的距离.
(1)因为某点到已知直线的垂线段只有一条,所以点到
直线的距离是唯一的;
(2)当这个点在已知直线上时,可看作点到直线的距离
为0;知3-讲 例4 如图,在三角形ABC中,∠ACB=90°,CD⊥
AB,垂足为D.若AC=4 cm,BC=3 cm,AB=
5 cm,则点A到直线BC的距离为______cm,点
B到直线AC的距离为______cm,点C到直线AB
的距离为______cm.432.4知3-讲导引:根据点到直线的距离的定义可知,点A到直线BC
的距离是线段AC的长,点B到直线AC的距离是线
段BC的长,点C到直线AB的距离是线段CD的长.
因为三角形ABC的面积S=
所以AC·BC=AB·CD,进而可得CD=2.4 cm.知3-讲 正确理解点到直线的距离及两点间的距离是解决
此类问题的关键.解决此类问题应注意:(1)点到直线
的距离是点到直线的垂线段的长度,而不是垂线,也
不是垂线段;(2)距离表示线段的长度,是一个数量,
与线段不能等同;(3)用垂线段的长度表示点到直线的
距离,其实质是点与垂足两点间的距离,体现了数形
结合思想.如图所示的是小凡同学在体育课上跳远后留下的
脚印,他的跳远成绩是线段________的长度.知3-练如图,其长能表示点到直线(线段)的距离的线段
的条数是( )
A.3
B.4
C.5
D.6知3-练3 点到直线的距离是指( )
A.直线外一点到这条直线的垂线的长度
B.直线外一点到这条直线上的任意一点的距离
C.直线外一点到这条直线的垂线段
D.直线外一点到这条直线的垂线段的长度知3-练
1. 垂线、垂直与垂线段的关系:
(1)区别:垂线是一条与已知直线垂直的直线;垂直
是两条直线之间的位置关系;垂线段是一条与已
知直线垂直的线段.
(2)联系:垂线段所在的直线是已知直线的垂线;垂
线段所在的直线与已知直线垂直.
2. 点到直线的距离:直线外一点到这条直线的垂线段
的长度,叫做点到直线的距离.
