5.1.4 同位角、内错角、同旁内角课件
文档属性
| 名称 | 5.1.4 同位角、内错角、同旁内角课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 579.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 00:00:00 | ||
图片预览






文档简介
课件29张PPT。第5章 相交线与平行线5.1 相交线第4课时 同位角、内错角、
同旁内角1课堂讲解同位角
内错角
同旁内角2课时流程逐点
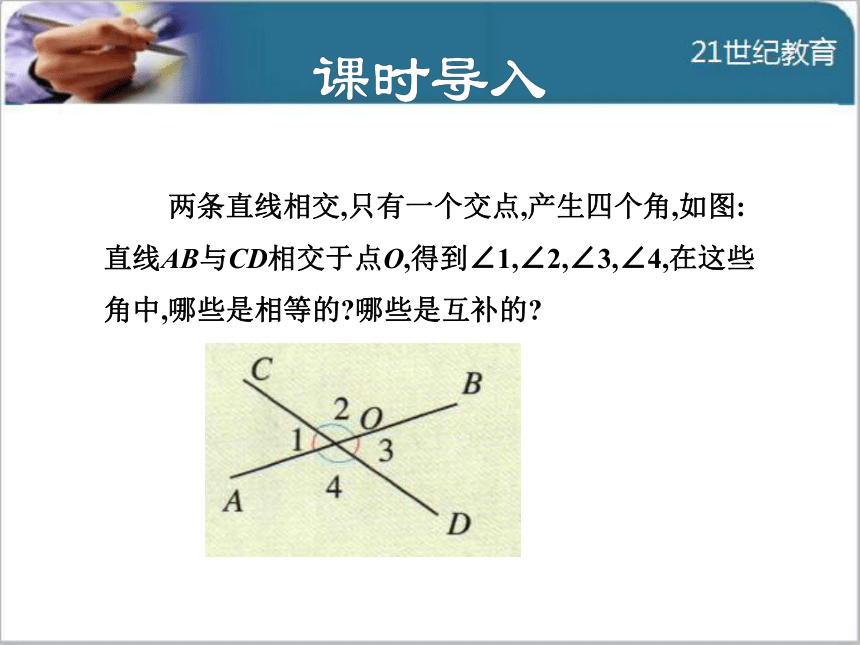
导讲练课堂小结作业提升 两条直线相交,只有一个交点,产生四个角,如图:
直线AB与CD相交于点O,得到∠1,∠2,∠3,∠4,在这些
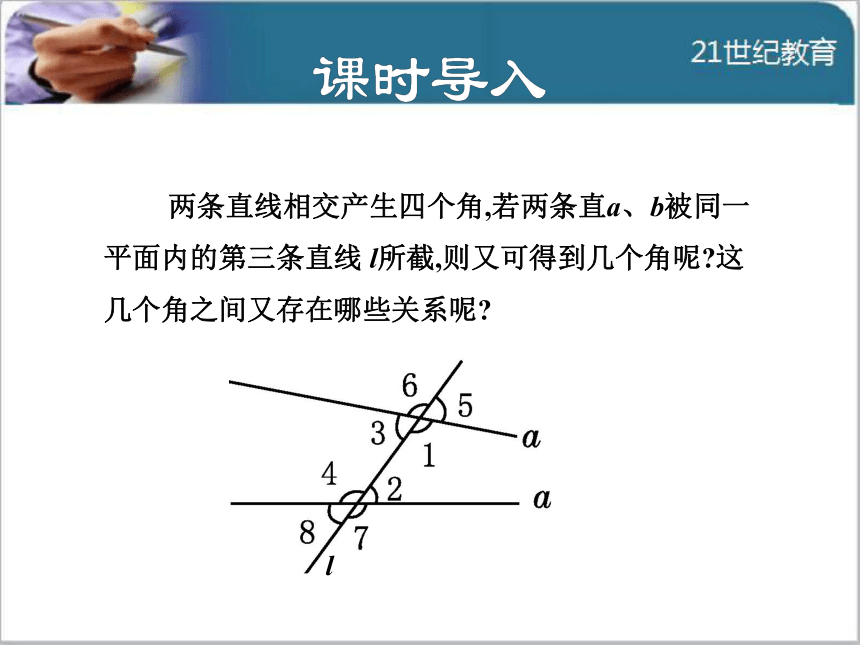
角中,哪些是相等的?哪些是互补的? 两条直线相交产生四个角,若两条直a、b被同一
平面内的第三条直线 l所截,则又可得到几个角呢?这
几个角之间又存在哪些关系呢?1知识点同位角 如图,直线AB,CD与EF相交(也可以说两条直线
AB,CD被第三条直线EF所 截),构成八个角. 我们
看那些没有公共顶点的
两个角的关系.知1-导 先看图中的∠1和∠5,这两个角分别在直线 AB,
CD的同一方(上方),并且都在直线的EF同侧(右侧),
具有这种位置关系的一对角叫做同位角
(corresponding angles).知1-导知1-讲定义:两条直线被第三条直线所截,得到的八个角中,
两个角分别在两条直线的同一方,并且都在第三条直
线的同侧,具有这种位置关系的一对角叫做同位角;
如图,∠1与∠2,∠3与∠4,∠5与∠6,∠7与∠8都
是同位角;画出∠1与∠2的两条边,可以发现这两个
角的边由三条线组成,
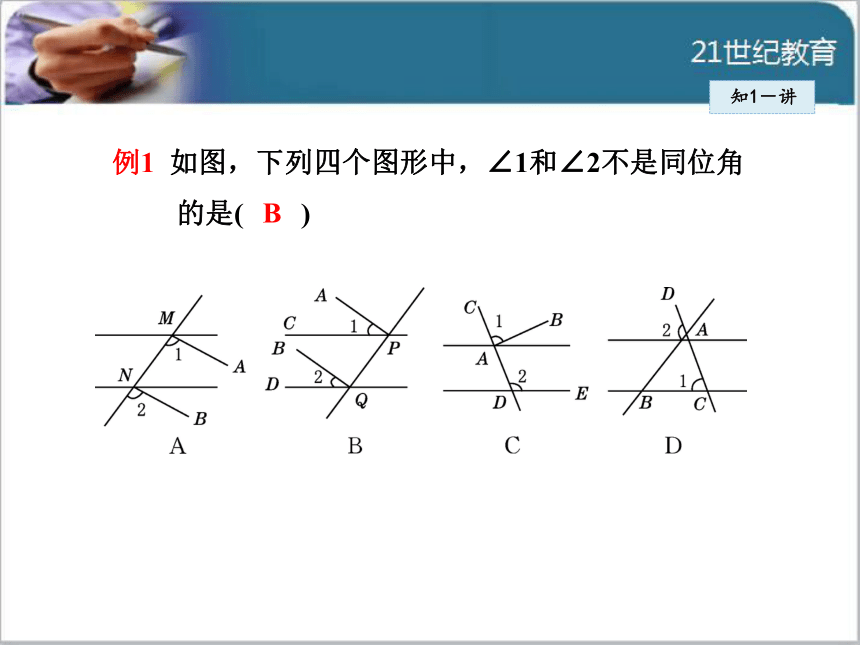
它的图像字母“F”.知1-讲 例1 如图,下列四个图形中,∠1和∠2不是同位角
的是( )
B知1-讲导引:根据同位角的概念,找出“三线”之后再看是否为
“F”形即可判定.选项B中的∠1与∠2的边有四条,
分别为PA,PC,QB,QD,不满足“三线”的条
件,故选项B中的∠1与∠2不是同位角;其他A,C,
D三项中的∠1,∠2均满足同位角的条件,故选B.知1-讲 判断“三线八角”中的两个角的位置关系时,必
须找出“哪两条直线被第三条直线所截”,即找准截
线是关键,找截线的实质就是找到相应两个角的顶点
所在的直线,如果这两个角的公共边恰好就是截线,
那么这两个角就是同位角.分别指出下列图中的同位角知1-练2 (中考·上海)如图,已知直线a、b被直线c所截,那
么∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5知1-练3 如图,在所标识的角中,同位角是( )
A.∠1和∠2 B.∠1和∠3
C.∠1和∠4 D.∠2和∠3知1-练4 下列图形中(如图),∠1和∠2是同位角的有( )
A.1个 B.2个 C.3个 D.4个知1-练2知识点内错角知2-讲定义:两条直线被第三条直线所截,得到的八个角中,
两个角都在两条直线之间,并且分别在第三条直线的
两侧,具有这种位置关系的一对角叫做内错角.如图,
∠1与∠2,∠3与∠4都是内错角.分别画出它们的两
条边,可发现组成这一对
角的“三条线”的图像字
母“Z”.知2-讲要点精析:
(1)内错角是成对出现的;并且是由三条直线组成的;
一边共线另两边不共线;
(2)内错角的顶点不是公共的;
(3)“内”可理解为夹在两直线之间;“错”可理解为
交错,即位于第三条直线的两侧;内错角的位置
关系具有“同内、异侧”的特征.知2-讲 例2 如图,试找出图中与∠2是同位角、内错角的角.
导引:在AF和AG被DE所截的这个基本图形中,可以
看出∠6和∠2处于“同一个位置”,因此,
∠2的同位角为∠6,∠2和∠8是内错角.
解: ∠2的同位角为∠6,∠2的内错角为∠8.
知2-讲 寻找一个角的同位角、内错角,首先应该把这个
角放在一个“三线八角”的基本图形中,其次不管是
同位角,还是内错角,它们具有一个共同特征,这两
个角有一对边在同一直线上,这条直线就是定义中的
“第三条直线”,而这两个角剩下的两边所在的直线
就是两条被截的直线 ;最后看这两个角的位置特征是
否满足同位角、内错角的位置特征:三边成“F ” 、
“Z ”形. 1 如图,两只手的食指和大拇指在同一个平面内,
它们构成的一对角可看成是__________.知2-练 2 (2015·贵阳)如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5知2-练 3 在我们常见的英文字母中,也存在着同位角、内错
角、同旁内角,在下面几个字母中,含有内错角最
少的字母是( )知2-练3知识点同旁内角知3-讲定义:两条直线被第三条直线所截,得到的八个角中,
两个角都在两条直线之间,但它们都在第三条直线的
同一旁.具有这种位置关系的一对角叫做同旁内角;
如图中的∠1与∠2,∠3与∠4都是同旁内角;分别画
出它们的两条边,可发现
组成这一对角的“三条线”
的图像字母“U”.知3-讲要点精析:
(1)同旁内角是成对出现的;并且是由三条直线组成
的;一边共线,另两边不共线;
(2)同旁内角的顶点不是公共的;
(3)“同旁”即在第三条直线的同一旁,“内”表示为
夹在两直线之间;同旁内角的位置关系具有“同
内、同侧”的特征.知3-讲如图,直线DE,BC被直线 AB所截.
(1)∠1和∠2, ∠1和∠3, ∠1和∠4 各是什么位置关
系的角?
(2) 如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?例3 知3-讲∠1和∠2是内错角, ∠1和∠3是同旁内角,
∠1和∠4是同位角.
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,
那么∠1=∠2.
因为∠4=∠3互补,即∠4 + ∠3 = 180°,
又因为∠1 = ∠4,所以∠1 + ∠3 = 180°,
即∠1和∠3 互补.答:知3-讲 本题运用定义法. 识别同位角、内错角、同旁内角
的关键是看两个角所涉及直线是否只有三条,并且有
没有一条边在同一直线(截线)上,如果没有,就不是;
如果有,再根据角的位置特征判断. 1 下列图形中∠1和∠2是同旁内角的是( )
知3-练 2 (2016·福州)如图,直线a、b被直线c所截,
∠1与∠2是( )
A.同位角
B.内错角
C.同旁内角
D.邻补角知3-练同位角、内错角、同旁内角的识别方法:
(1)确定“三线”:公共边为截线,另外两边为被截线.
(2)区分位置关系:同位角:被截直线的同一方,截线
的同侧;内错角:被截直线之间,截线的两侧;同
旁内角:被截直线之间,截线的同旁.
同旁内角1课堂讲解同位角
内错角
同旁内角2课时流程逐点
导讲练课堂小结作业提升 两条直线相交,只有一个交点,产生四个角,如图:
直线AB与CD相交于点O,得到∠1,∠2,∠3,∠4,在这些
角中,哪些是相等的?哪些是互补的? 两条直线相交产生四个角,若两条直a、b被同一
平面内的第三条直线 l所截,则又可得到几个角呢?这
几个角之间又存在哪些关系呢?1知识点同位角 如图,直线AB,CD与EF相交(也可以说两条直线
AB,CD被第三条直线EF所 截),构成八个角. 我们
看那些没有公共顶点的
两个角的关系.知1-导 先看图中的∠1和∠5,这两个角分别在直线 AB,
CD的同一方(上方),并且都在直线的EF同侧(右侧),
具有这种位置关系的一对角叫做同位角
(corresponding angles).知1-导知1-讲定义:两条直线被第三条直线所截,得到的八个角中,
两个角分别在两条直线的同一方,并且都在第三条直
线的同侧,具有这种位置关系的一对角叫做同位角;
如图,∠1与∠2,∠3与∠4,∠5与∠6,∠7与∠8都
是同位角;画出∠1与∠2的两条边,可以发现这两个
角的边由三条线组成,
它的图像字母“F”.知1-讲 例1 如图,下列四个图形中,∠1和∠2不是同位角
的是( )
B知1-讲导引:根据同位角的概念,找出“三线”之后再看是否为
“F”形即可判定.选项B中的∠1与∠2的边有四条,
分别为PA,PC,QB,QD,不满足“三线”的条
件,故选项B中的∠1与∠2不是同位角;其他A,C,
D三项中的∠1,∠2均满足同位角的条件,故选B.知1-讲 判断“三线八角”中的两个角的位置关系时,必
须找出“哪两条直线被第三条直线所截”,即找准截
线是关键,找截线的实质就是找到相应两个角的顶点
所在的直线,如果这两个角的公共边恰好就是截线,
那么这两个角就是同位角.分别指出下列图中的同位角知1-练2 (中考·上海)如图,已知直线a、b被直线c所截,那
么∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5知1-练3 如图,在所标识的角中,同位角是( )
A.∠1和∠2 B.∠1和∠3
C.∠1和∠4 D.∠2和∠3知1-练4 下列图形中(如图),∠1和∠2是同位角的有( )
A.1个 B.2个 C.3个 D.4个知1-练2知识点内错角知2-讲定义:两条直线被第三条直线所截,得到的八个角中,
两个角都在两条直线之间,并且分别在第三条直线的
两侧,具有这种位置关系的一对角叫做内错角.如图,
∠1与∠2,∠3与∠4都是内错角.分别画出它们的两
条边,可发现组成这一对
角的“三条线”的图像字
母“Z”.知2-讲要点精析:
(1)内错角是成对出现的;并且是由三条直线组成的;
一边共线另两边不共线;
(2)内错角的顶点不是公共的;
(3)“内”可理解为夹在两直线之间;“错”可理解为
交错,即位于第三条直线的两侧;内错角的位置
关系具有“同内、异侧”的特征.知2-讲 例2 如图,试找出图中与∠2是同位角、内错角的角.
导引:在AF和AG被DE所截的这个基本图形中,可以
看出∠6和∠2处于“同一个位置”,因此,
∠2的同位角为∠6,∠2和∠8是内错角.
解: ∠2的同位角为∠6,∠2的内错角为∠8.
知2-讲 寻找一个角的同位角、内错角,首先应该把这个
角放在一个“三线八角”的基本图形中,其次不管是
同位角,还是内错角,它们具有一个共同特征,这两
个角有一对边在同一直线上,这条直线就是定义中的
“第三条直线”,而这两个角剩下的两边所在的直线
就是两条被截的直线 ;最后看这两个角的位置特征是
否满足同位角、内错角的位置特征:三边成“F ” 、
“Z ”形. 1 如图,两只手的食指和大拇指在同一个平面内,
它们构成的一对角可看成是__________.知2-练 2 (2015·贵阳)如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5知2-练 3 在我们常见的英文字母中,也存在着同位角、内错
角、同旁内角,在下面几个字母中,含有内错角最
少的字母是( )知2-练3知识点同旁内角知3-讲定义:两条直线被第三条直线所截,得到的八个角中,
两个角都在两条直线之间,但它们都在第三条直线的
同一旁.具有这种位置关系的一对角叫做同旁内角;
如图中的∠1与∠2,∠3与∠4都是同旁内角;分别画
出它们的两条边,可发现
组成这一对角的“三条线”
的图像字母“U”.知3-讲要点精析:
(1)同旁内角是成对出现的;并且是由三条直线组成
的;一边共线,另两边不共线;
(2)同旁内角的顶点不是公共的;
(3)“同旁”即在第三条直线的同一旁,“内”表示为
夹在两直线之间;同旁内角的位置关系具有“同
内、同侧”的特征.知3-讲如图,直线DE,BC被直线 AB所截.
(1)∠1和∠2, ∠1和∠3, ∠1和∠4 各是什么位置关
系的角?
(2) 如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?例3 知3-讲∠1和∠2是内错角, ∠1和∠3是同旁内角,
∠1和∠4是同位角.
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,
那么∠1=∠2.
因为∠4=∠3互补,即∠4 + ∠3 = 180°,
又因为∠1 = ∠4,所以∠1 + ∠3 = 180°,
即∠1和∠3 互补.答:知3-讲 本题运用定义法. 识别同位角、内错角、同旁内角
的关键是看两个角所涉及直线是否只有三条,并且有
没有一条边在同一直线(截线)上,如果没有,就不是;
如果有,再根据角的位置特征判断. 1 下列图形中∠1和∠2是同旁内角的是( )
知3-练 2 (2016·福州)如图,直线a、b被直线c所截,
∠1与∠2是( )
A.同位角
B.内错角
C.同旁内角
D.邻补角知3-练同位角、内错角、同旁内角的识别方法:
(1)确定“三线”:公共边为截线,另外两边为被截线.
(2)区分位置关系:同位角:被截直线的同一方,截线
的同侧;内错角:被截直线之间,截线的两侧;同
旁内角:被截直线之间,截线的同旁.
