5.2.1 平行线课件
图片预览











文档简介
课件36张PPT。第五章 相交线与平行线5.2 平行线及其判定第1课时 平行线1课堂讲解平行线的定义
平行线的画法
平行线的基本事实
平行线的传递性2课时流程逐点
导讲练课堂小结作业提升 如图所示,是两名正在滑雪的运动员.据说,早在
5000年前,人们就把滑雪作为雪地上流行的一种运动
方式,今天,滑雪在许多国家和地区都是一项十分普
及的运动.滑雪运动最关键的是要保持两只雪橇板的
平行!
你知道什么是平
行线吗?平行线有什么性
质吗?请学习下面的知识
吧!1知识点平行线的定义思考
如图,分别将木条a,b与木条c钉在一起,并把它
们想象成在同一平面内两端可以无限延伸的三条直线.
转动a,直线a从在c的左侧与直线b相交逐步变为在c的
右侧与b相交. 想象一下,在这个过程中, 有没有直线
a与直线b不相交的位置呢?知1-导知1-导知1-导 可以发现,在木条转动过程中,存在直线a 与b
不相交的情形,这时我们说直线a与b互相平 行
(parallel),记作a//b.
平行线在生活中是很常见的, 你还能举出其他一
些例子吗?
知1-讲定义:在同一平面内,不相交的两条直线叫做平行线.
表示方法:用“∥”表示平行,如图,记作“AB∥CD”
或“CD∥AB”,读作“AB平行于CD”或“CD平行于
AB”.
知1-讲 例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
导引:(1)没有强调两条直线在同一平面内;
(2)两条线段平行应该是这两条线段所在的直线
平行.
知1-讲解:(1)不正确;
理由:根据定义,它缺少了“在同一平面内”
这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”,
而不是“线段”.知1-讲平行线的定义有三个特征:
一是在同一平面内;
二是不相交;
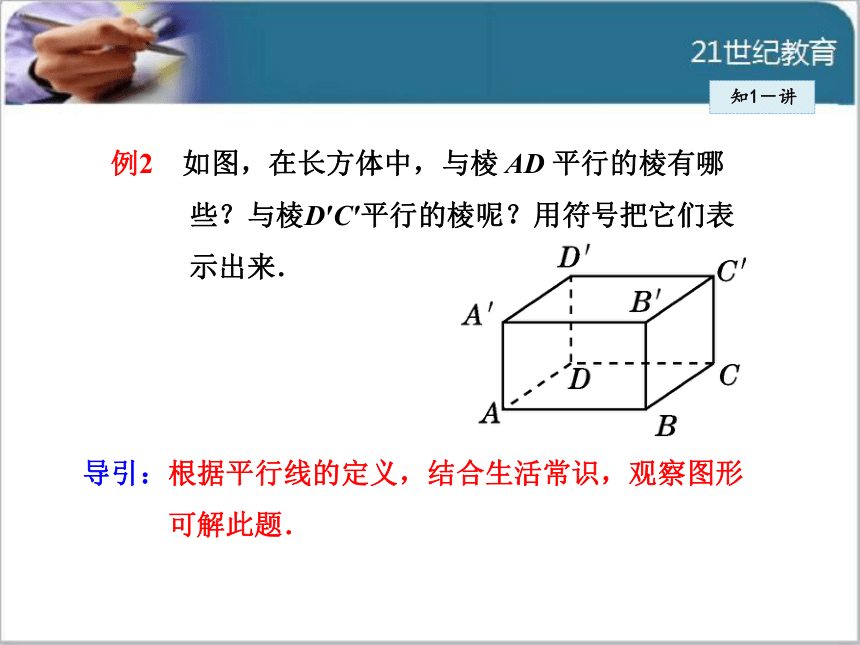
三是都是直线;三者缺一不可.知1-讲 例2 如图,在长方体中,与棱 AD 平行的棱有哪
些?与棱D′C′平行的棱呢?用符号把它们表
示出来.
导引:根据平行线的定义,结合生活常识,观察图形
可解此题.知1-讲解:与棱AD平行的棱有A′D′,B′C′,BC,
记作AD∥A′D′,AD∥B′C′,AD∥BC.
与棱D′C′平行的棱有DC,AB,A′B′,
记作D′C′∥DC, D′C′∥AB, D′C′∥A′B′.知1-讲找平行线要注意两点:
(1)在同一平面内;
(2)不相交(无限延伸).1 在同一平面内,两条直线的位置关系是( )
A.平行或垂直
B.平行或相交
C.垂直或相交
D.平行、垂直或相交知1-练2 如图,将一张长方形纸对折三次,则产生的折痕
与折痕间的位置关系是( )
A.平行 B.垂直
C.平行或垂直 D.无法确定知1-练3 a,b,c是平面内任意三条直线,交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
知1-练2知识点 平行线的画法知2-讲过直线外一点画已知直线的平行线的步骤:
一落:把三角尺的一边落在已知直线上;
二靠:紧靠三角尺的另一边放一直尺;
三移:把这个三角尺沿着直尺移动使其经过已知点;
四画:沿三角尺的一边画直线.此直线即为已知直
线的平行线.知2-讲 例3 如图,过P点作PQ∥AB交BC于Q,作PM∥
AC交AB于M.
导引:过直线外一点画已知
直线的平行线,要按一
“落”,二“靠”,三“移”,
四“画”的步骤进行.
解:如图. 注意“移”时经过点的边是三角尺落在已知直
线上的那一边,而不是任意一边,利用直尺和三角
尺画过直线外一点的已知直线的平行线是几何画图
的基本技能之一.知2-讲知2-讲例4 如图,在下面的网格中经过点C画与线段AB
平行的直线 l1,再经过点B画一条与线段AB
垂直的直线 l2.
解:如图. 网格中作直线的平行线或垂线时,不需要借
助尺规,直接根据网格的特点作图即可.知2-讲1 读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与
直线AB平行;
(2)直线AB,CD是相交直线,点P是直线AB,CD
外的一点,直线EF经过点 P且与直线AB平行,
与直线CD相交于点E.知2-练2 如图,经过点P画一条直线使它与l平行.
画法:(1)一落:把三角尺的一边落在________上;
(2)二______:紧靠三角尺的另一边放一直尺AB; 知2-练(3)三________:把三角尺沿直尺的边移到三角尺的
第一边恰好经过点P的位置;
(4)四________:沿三角尺的这一边画直线 l′.l′就是
所要作的过点P与直线l平行的直线.
知2-练3知识点平行线的基本事实知3-导 在图转动木条a的过程中,有几个位置使得直线
a与b平行?如图,过点B画直线 a的平行线,能画出
几条?再过点C画直线a的平 行线,它和前面过点B
画出的直线平行吗?知3-导通过观察和画图,可以发现一个基本事实(平行公理):
经过直线外一点,有且只有一条直线与这条直线平行. 知3-讲 例5 下列说法:①过一点有且只有一条直线与已
知直线平行;②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条
直线平行.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
导引:过直线外一点可以画一条直线与已知直线平行,
而过直线上一点画不出与该直线平行的直线;
一条直线的平行线有无数条,故只有③正确.
C 对于此类辨析题,要正确解答,必须要抓住
相关的内容,特别是关键字词及其重要特征,要
在比较中理解,再在理解的基础上进行记忆.知3-讲 如图,当风车的一片叶子AB旋转到与地面MN平
行时,叶子CD所在的直线与地面MN________,
理由是__________________.知3-练知3-练2 在同一平面内,下列说法正确的有( )
①过两点有且只有一条直线;
②两条直线有且只有一个交点;
③过一点有且只有一条直线与已知直线相交;
④过一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个4知识点平行线的传递性知4-讲平行公理的推论:如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.简称:同平行于
第三条直线的两直线平行.
表达方式:如果a∥c,b∥c,那么a∥b.
平行公理的推论:可用来判定两直线平行.知4-讲 例6 如图,P是三角形ABC内部的任意一点.
(1)过P点向左画射线PM∥BC交AB于点M,过
P点向右画射线PN∥BC交AC于点N;
(2)在(1)中画出的图形中,∠MPN的度数一定等
于180°,你能说明其中的道理吗?知4-讲导引:在(1)中,按照过直线外一点画已知直线的平行线
的方法画图即可.在(2)中,要说明∠MPN=180°,
可转化为说明点M, P, N在同一条直线上.
解:(1)画出的射线PM,PN,如上页图.
(2)因为射线PM∥BC,射线PN∥BC,
所以直线PM∥BC,直线PN∥BC.
所以直线PM与直线PN是同一条直线(过直线外一
点有且只有一条直线与这条直线平行),
即点M, P, N在同一条直线上.所以∠MPN=180°. 本题运用转化思想,把说明∠MPN=180°转
化为说明点M,P,N在同一条直线上,进而把问题
转化为利用有关平行线的基本事实说明直线PM与直
线PN是同一条直线.知4-讲下列说法正确的有( )
①不相交的两条直线是平行线;
②在同一平面内,两条不重合的直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;
④若a∥b,b∥c,且a与c不重合,则a与c不相交.
A.1个 B.2个 C.3个 D.4个知4-练11. 平行线的定义及平面内两直线的位置关系
平行线的定义包含缺一不可的三个条件:
①在同一平面内;②不相交;③都是直线.
2. 平行线的画法
一落、二靠、三移、四画
3. 平行线的基本事实及其推论
(1)“有且只有”强调直线的存在性和唯一性;
(2)前提条件“经过直线外一点”,若点在直线上,
不可能有平行线.
平行线的画法
平行线的基本事实
平行线的传递性2课时流程逐点
导讲练课堂小结作业提升 如图所示,是两名正在滑雪的运动员.据说,早在
5000年前,人们就把滑雪作为雪地上流行的一种运动
方式,今天,滑雪在许多国家和地区都是一项十分普
及的运动.滑雪运动最关键的是要保持两只雪橇板的
平行!
你知道什么是平
行线吗?平行线有什么性
质吗?请学习下面的知识
吧!1知识点平行线的定义思考
如图,分别将木条a,b与木条c钉在一起,并把它
们想象成在同一平面内两端可以无限延伸的三条直线.
转动a,直线a从在c的左侧与直线b相交逐步变为在c的
右侧与b相交. 想象一下,在这个过程中, 有没有直线
a与直线b不相交的位置呢?知1-导知1-导知1-导 可以发现,在木条转动过程中,存在直线a 与b
不相交的情形,这时我们说直线a与b互相平 行
(parallel),记作a//b.
平行线在生活中是很常见的, 你还能举出其他一
些例子吗?
知1-讲定义:在同一平面内,不相交的两条直线叫做平行线.
表示方法:用“∥”表示平行,如图,记作“AB∥CD”
或“CD∥AB”,读作“AB平行于CD”或“CD平行于
AB”.
知1-讲 例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
导引:(1)没有强调两条直线在同一平面内;
(2)两条线段平行应该是这两条线段所在的直线
平行.
知1-讲解:(1)不正确;
理由:根据定义,它缺少了“在同一平面内”
这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”,
而不是“线段”.知1-讲平行线的定义有三个特征:
一是在同一平面内;
二是不相交;
三是都是直线;三者缺一不可.知1-讲 例2 如图,在长方体中,与棱 AD 平行的棱有哪
些?与棱D′C′平行的棱呢?用符号把它们表
示出来.
导引:根据平行线的定义,结合生活常识,观察图形
可解此题.知1-讲解:与棱AD平行的棱有A′D′,B′C′,BC,
记作AD∥A′D′,AD∥B′C′,AD∥BC.
与棱D′C′平行的棱有DC,AB,A′B′,
记作D′C′∥DC, D′C′∥AB, D′C′∥A′B′.知1-讲找平行线要注意两点:
(1)在同一平面内;
(2)不相交(无限延伸).1 在同一平面内,两条直线的位置关系是( )
A.平行或垂直
B.平行或相交
C.垂直或相交
D.平行、垂直或相交知1-练2 如图,将一张长方形纸对折三次,则产生的折痕
与折痕间的位置关系是( )
A.平行 B.垂直
C.平行或垂直 D.无法确定知1-练3 a,b,c是平面内任意三条直线,交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
知1-练2知识点 平行线的画法知2-讲过直线外一点画已知直线的平行线的步骤:
一落:把三角尺的一边落在已知直线上;
二靠:紧靠三角尺的另一边放一直尺;
三移:把这个三角尺沿着直尺移动使其经过已知点;
四画:沿三角尺的一边画直线.此直线即为已知直
线的平行线.知2-讲 例3 如图,过P点作PQ∥AB交BC于Q,作PM∥
AC交AB于M.
导引:过直线外一点画已知
直线的平行线,要按一
“落”,二“靠”,三“移”,
四“画”的步骤进行.
解:如图. 注意“移”时经过点的边是三角尺落在已知直
线上的那一边,而不是任意一边,利用直尺和三角
尺画过直线外一点的已知直线的平行线是几何画图
的基本技能之一.知2-讲知2-讲例4 如图,在下面的网格中经过点C画与线段AB
平行的直线 l1,再经过点B画一条与线段AB
垂直的直线 l2.
解:如图. 网格中作直线的平行线或垂线时,不需要借
助尺规,直接根据网格的特点作图即可.知2-讲1 读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与
直线AB平行;
(2)直线AB,CD是相交直线,点P是直线AB,CD
外的一点,直线EF经过点 P且与直线AB平行,
与直线CD相交于点E.知2-练2 如图,经过点P画一条直线使它与l平行.
画法:(1)一落:把三角尺的一边落在________上;
(2)二______:紧靠三角尺的另一边放一直尺AB; 知2-练(3)三________:把三角尺沿直尺的边移到三角尺的
第一边恰好经过点P的位置;
(4)四________:沿三角尺的这一边画直线 l′.l′就是
所要作的过点P与直线l平行的直线.
知2-练3知识点平行线的基本事实知3-导 在图转动木条a的过程中,有几个位置使得直线
a与b平行?如图,过点B画直线 a的平行线,能画出
几条?再过点C画直线a的平 行线,它和前面过点B
画出的直线平行吗?知3-导通过观察和画图,可以发现一个基本事实(平行公理):
经过直线外一点,有且只有一条直线与这条直线平行. 知3-讲 例5 下列说法:①过一点有且只有一条直线与已
知直线平行;②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条
直线平行.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
导引:过直线外一点可以画一条直线与已知直线平行,
而过直线上一点画不出与该直线平行的直线;
一条直线的平行线有无数条,故只有③正确.
C 对于此类辨析题,要正确解答,必须要抓住
相关的内容,特别是关键字词及其重要特征,要
在比较中理解,再在理解的基础上进行记忆.知3-讲 如图,当风车的一片叶子AB旋转到与地面MN平
行时,叶子CD所在的直线与地面MN________,
理由是__________________.知3-练知3-练2 在同一平面内,下列说法正确的有( )
①过两点有且只有一条直线;
②两条直线有且只有一个交点;
③过一点有且只有一条直线与已知直线相交;
④过一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个4知识点平行线的传递性知4-讲平行公理的推论:如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.简称:同平行于
第三条直线的两直线平行.
表达方式:如果a∥c,b∥c,那么a∥b.
平行公理的推论:可用来判定两直线平行.知4-讲 例6 如图,P是三角形ABC内部的任意一点.
(1)过P点向左画射线PM∥BC交AB于点M,过
P点向右画射线PN∥BC交AC于点N;
(2)在(1)中画出的图形中,∠MPN的度数一定等
于180°,你能说明其中的道理吗?知4-讲导引:在(1)中,按照过直线外一点画已知直线的平行线
的方法画图即可.在(2)中,要说明∠MPN=180°,
可转化为说明点M, P, N在同一条直线上.
解:(1)画出的射线PM,PN,如上页图.
(2)因为射线PM∥BC,射线PN∥BC,
所以直线PM∥BC,直线PN∥BC.
所以直线PM与直线PN是同一条直线(过直线外一
点有且只有一条直线与这条直线平行),
即点M, P, N在同一条直线上.所以∠MPN=180°. 本题运用转化思想,把说明∠MPN=180°转
化为说明点M,P,N在同一条直线上,进而把问题
转化为利用有关平行线的基本事实说明直线PM与直
线PN是同一条直线.知4-讲下列说法正确的有( )
①不相交的两条直线是平行线;
②在同一平面内,两条不重合的直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;
④若a∥b,b∥c,且a与c不重合,则a与c不相交.
A.1个 B.2个 C.3个 D.4个知4-练11. 平行线的定义及平面内两直线的位置关系
平行线的定义包含缺一不可的三个条件:
①在同一平面内;②不相交;③都是直线.
2. 平行线的画法
一落、二靠、三移、四画
3. 平行线的基本事实及其推论
(1)“有且只有”强调直线的存在性和唯一性;
(2)前提条件“经过直线外一点”,若点在直线上,
不可能有平行线.
