5.2.2 平行线的判定——利用“同位角、第三直线”课件
文档属性
| 名称 | 5.2.2 平行线的判定——利用“同位角、第三直线”课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 00:00:00 | ||
图片预览








文档简介
课件26张PPT。第五章 相交线与平行线5.2 平行线及其判定第2课时 平行线的判定——利用
“同位角、第三直线”1课堂讲解由“同位角相等”判定两直线平行
由“第三直线”判定两直线平行2课时流程逐点
导讲练课堂小结作业提升 要判定两条直线互相平行,我们无法依据它
的定义,判断这两条直线在无限延长的过程中是否
永远不相交.那么从前面画平行线的过程,我们可
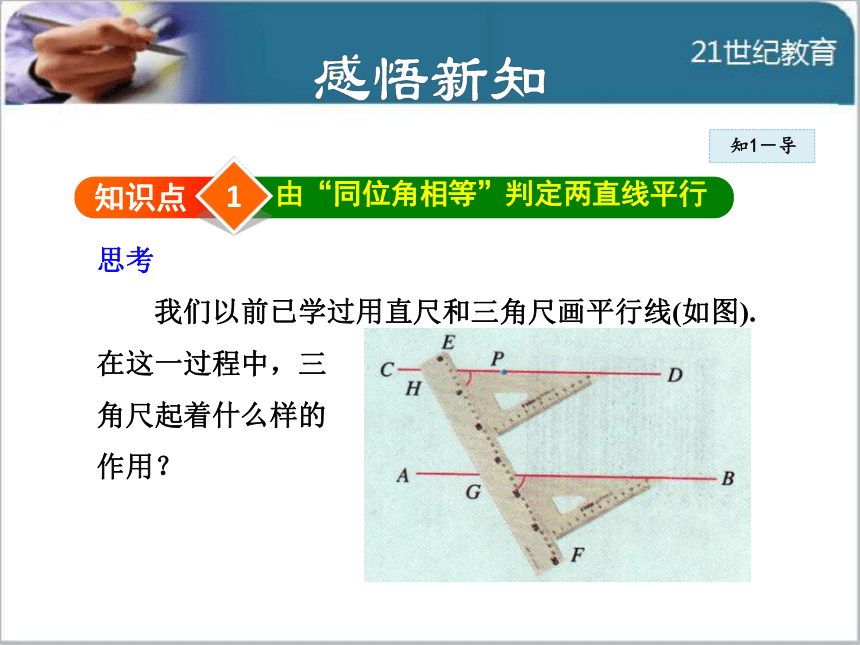
以得到什么启示呢?1知识点由“同位角相等”判定两直线平行知1-导思考
我们以前已学过用直尺和三角尺画平行线(如图).
在这一过程中,三
角尺起着什么样的
作用?知1-导 简化上页图得到下图.可以看出,画直线AB的
平行线CD,实际上就是过点P画与∠2相等的∠1,
而∠2和∠1正是直线
AB,CD被直线EF截
得的同位角.这说明,
如果同位角相等,
那么AB//CD.知1-导 一般地,有如下利用同位角判定两条直线平行的
方法:
判定方法1 两条直线被第三条直线所截,如果同位角
相等,那么这两条 直线平行.
简单说成:同位角相等,两直线平行.知1-讲 例1 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
导引:要判定哪两条直线平行,就是要确定∠1,∠2
是哪两条直线被第三条直线
截得到的同位角, 即找出∠1,
∠2除公共边所在直线外的另
两边所在直线.
C知1-讲利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线
所截形成的;再根据“同位角相等,两直线平行”推
导出这两条直线平行.知1-讲 例2 如图,已知直线AB,CD被直线EF所截,
∠1+∠2=180°.
AB与CD平行吗?
请说明理由.
导引:要说明AB与CD平行,需找出AB,CD被第三条
直线所截形成的一组同位角相等,即要说明∠1
=∠3即可;要说明∠1=∠3,由于已知∠1+
∠2=180°,因此只需说明∠2+∠3=180°即
可,这可由邻补角定义得出.知1-讲解: AB∥CD.理由如下:
∵∠1+∠2=180°,
∠2+∠3=180°(邻补角定义),
∴∠1=∠3(同角的补角相等).
∴AB∥CD(同位角相等,两直线平行).
知1-讲在同一平面内,如果两条直线都垂直于同 一条直
线,那么这两条直线平行吗?为什么?
垂直总与直角联系在一起,进而用判断 两条直线
平行的方法进行判定. 例3 分析:知1-讲这两条直线平行. 理由如下:
如图.
∵a⊥b,
∴∠1=90°.
同理∠2=90°.
∴∠1=∠2 .
∵ ∠1和∠2 是同位角,
∴b∥c (同位角相等,两直线平行).答:知1-讲 判断两条直线是否平行,可以找出这两条直
线被第三条直线所截得到的一对同位角,并利用
相关角的条件判断其是否相等,如果相等,那么
这两条直线平行.知1-练如图,BE是AB的延长线.
由∠CBE= ∠A 可以判定哪两条直线平行? 根据是什么?1知1-练如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
2知1-练如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
3知1-练如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC B.AB∥CD
C.CA平分∠BCD D.AC平分∠BAD
42知识点由“第三直线”判定两直线平行知2-讲如图,你能说出木工用图中的角尺画平行线的道理吗?知2-讲平行于同一条直线的两直线平行.知2-讲如图所示,直线AB、CD是一条河的两岸,并AB∥CD,点E为直线AB、CD外一点.现想过点E作CD的平行线,则只需过点E作岸AB的平行线即可.其理由是什么?例4 知2-讲利用平行线的性质,把实际问题转化为数学
问题回答.解:分析:理由是(1)过直线外一点有且只有一条直线与
已知直线平行.(2)如果两条直线都与第三条
直线平行,那么这两条直线也互相平行.知2-讲 在同一平面内和一条直线平行的直线也互相
平行.知2-练如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB________CD.
1知2-练在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )
A.互相平行 B.互相垂直
C.共线 D.互相平行或共线
2知2-练三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定3判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”判定.
“同位角、第三直线”1课堂讲解由“同位角相等”判定两直线平行
由“第三直线”判定两直线平行2课时流程逐点
导讲练课堂小结作业提升 要判定两条直线互相平行,我们无法依据它
的定义,判断这两条直线在无限延长的过程中是否
永远不相交.那么从前面画平行线的过程,我们可
以得到什么启示呢?1知识点由“同位角相等”判定两直线平行知1-导思考
我们以前已学过用直尺和三角尺画平行线(如图).
在这一过程中,三
角尺起着什么样的
作用?知1-导 简化上页图得到下图.可以看出,画直线AB的
平行线CD,实际上就是过点P画与∠2相等的∠1,
而∠2和∠1正是直线
AB,CD被直线EF截
得的同位角.这说明,
如果同位角相等,
那么AB//CD.知1-导 一般地,有如下利用同位角判定两条直线平行的
方法:
判定方法1 两条直线被第三条直线所截,如果同位角
相等,那么这两条 直线平行.
简单说成:同位角相等,两直线平行.知1-讲 例1 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
导引:要判定哪两条直线平行,就是要确定∠1,∠2
是哪两条直线被第三条直线
截得到的同位角, 即找出∠1,
∠2除公共边所在直线外的另
两边所在直线.
C知1-讲利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线
所截形成的;再根据“同位角相等,两直线平行”推
导出这两条直线平行.知1-讲 例2 如图,已知直线AB,CD被直线EF所截,
∠1+∠2=180°.
AB与CD平行吗?
请说明理由.
导引:要说明AB与CD平行,需找出AB,CD被第三条
直线所截形成的一组同位角相等,即要说明∠1
=∠3即可;要说明∠1=∠3,由于已知∠1+
∠2=180°,因此只需说明∠2+∠3=180°即
可,这可由邻补角定义得出.知1-讲解: AB∥CD.理由如下:
∵∠1+∠2=180°,
∠2+∠3=180°(邻补角定义),
∴∠1=∠3(同角的补角相等).
∴AB∥CD(同位角相等,两直线平行).
知1-讲在同一平面内,如果两条直线都垂直于同 一条直
线,那么这两条直线平行吗?为什么?
垂直总与直角联系在一起,进而用判断 两条直线
平行的方法进行判定. 例3 分析:知1-讲这两条直线平行. 理由如下:
如图.
∵a⊥b,
∴∠1=90°.
同理∠2=90°.
∴∠1=∠2 .
∵ ∠1和∠2 是同位角,
∴b∥c (同位角相等,两直线平行).答:知1-讲 判断两条直线是否平行,可以找出这两条直
线被第三条直线所截得到的一对同位角,并利用
相关角的条件判断其是否相等,如果相等,那么
这两条直线平行.知1-练如图,BE是AB的延长线.
由∠CBE= ∠A 可以判定哪两条直线平行? 根据是什么?1知1-练如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
2知1-练如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
3知1-练如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC B.AB∥CD
C.CA平分∠BCD D.AC平分∠BAD
42知识点由“第三直线”判定两直线平行知2-讲如图,你能说出木工用图中的角尺画平行线的道理吗?知2-讲平行于同一条直线的两直线平行.知2-讲如图所示,直线AB、CD是一条河的两岸,并AB∥CD,点E为直线AB、CD外一点.现想过点E作CD的平行线,则只需过点E作岸AB的平行线即可.其理由是什么?例4 知2-讲利用平行线的性质,把实际问题转化为数学
问题回答.解:分析:理由是(1)过直线外一点有且只有一条直线与
已知直线平行.(2)如果两条直线都与第三条
直线平行,那么这两条直线也互相平行.知2-讲 在同一平面内和一条直线平行的直线也互相
平行.知2-练如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB________CD.
1知2-练在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )
A.互相平行 B.互相垂直
C.共线 D.互相平行或共线
2知2-练三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定3判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”判定.
