5.2.3 平行线的判定——利用“内错角、同旁内角”课件
文档属性
| 名称 | 5.2.3 平行线的判定——利用“内错角、同旁内角”课件 |  | |
| 格式 | zip | ||
| 文件大小 | 413.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 14:46:57 | ||
图片预览







文档简介
课件28张PPT。第五章 相交线与平行线5.2 平行线及其判定第3课时 平行线的判定——利用
“内错角、同旁内角”1课堂讲解由“内错角相等”判定两直线平行、
由“同旁内角互补”判定两直线平行2课时流程逐点
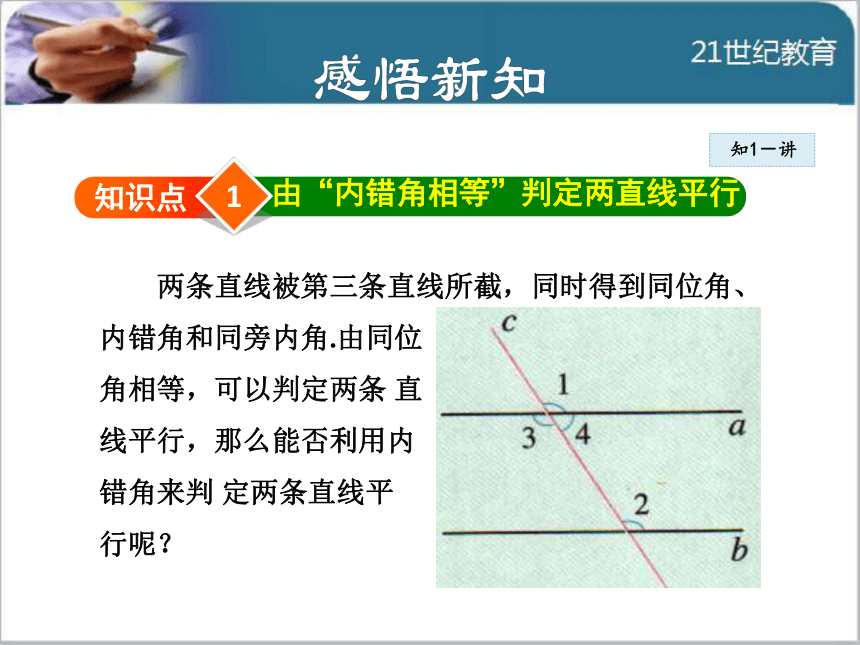
导讲练课堂小结作业提升1知识点由“内错角相等”判定两直线平行知1-讲 两条直线被第三条直线所截,同时得到同位角、
内错角和同旁内角.由同位
角相等,可以判定两条 直
线平行,那么能否利用内
错角来判 定两条直线平
行呢?知1-讲判定方法2 两条直线被第三条直线所截,如果内错
角相等,那么这两条 直线平行.
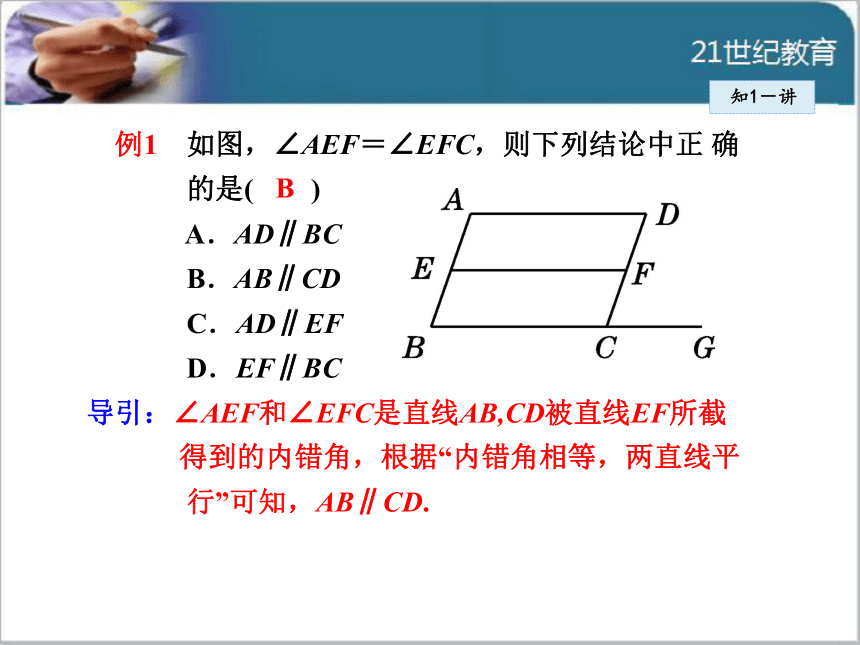
简单说成:内错角相等,两直线平行.知1-讲 例1 如图,∠AEF=∠EFC,则下列结论中正 确
的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
导引:∠AEF和∠EFC是直线AB,CD被直线EF所截
得到的内错角,根据“内错角相等,两直线平
行”可知,AB∥CD.B知1-讲利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,
看其是否相等.若相等,则两条直线平行.知1-讲 例2 如图,已知∠ADE=60°,DF平分∠ADE,
∠1=30°,试
说明:DF∥BE.
导引:要想说明DF∥BE,可通过说明∠1=∠EDF
来实现,由于∠1=30°,所以只需求出∠EDF
=30°,而这个结论可通过DF是∠ADE的平分
线来求得.知1-讲解:∵DF平分∠ADE(已知),
∴∠EDF= ∠ADE(角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE(内错角相等,两直线平行).知1-讲 要判定两直线平行可以通过说明同位角相等
或内错角相等来实现,至于到底选用同位角还是
选用内错角,要看具体的题目,要尽可能与已知
条件联系.知1-练如图,已知∠1=120°,当∠2=________时,a∥b,理由是________________________________________.1知1-练(2015·福州)下列图形中,由∠1=∠2能得到AB∥CD的是( )
2知1-练如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2 B.∠2=∠3
C.∠3=∠4 D.∠4=∠5
32知识点由“同旁内角互补”判定两直线平行知2-讲探究
遇到一个新问题时,常常把它转化为已知的(或已
解决的)问题. 这一节中,我们是怎样利用“同位角相
等,两直线平行”得到“内错角相 等,两直线平行”
的?你能利用“同位角相等,两直线平行”或“内错
角相等,两直线平行”得到“同旁内角互补,两直线
平行”吗?知2-讲两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
简称:同旁内角互补,两直线平行.?
表达方式:如图:
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两
直线平行).知2-讲 例3 如图,直线AE,CD相交于点O,如果∠A=
110°,∠1=70°,就可以说明AB∥CD,
这是为什么?
?
导引:由题意可知∠1=∠AOD=70°,又∵∠A=
110°,∴∠A+∠AOD=180°,故 AB∥CD.
知2-讲解:因为∠1=∠AOD(对顶角相等),∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).
知2-讲1.本题运用数形结合思想.平行线的判定是由角之间
的数量关系到“形”的判定.要判定两直线平行,可
围绕截线找同位角、内错角或同旁内角,若同位角
相等、内错角相等或同旁内角互补,则两直线平行.
2.用同位角相等、内错角相等或同旁内角互补中的一
个方法说明两直线平行时,一般都要通过结合对顶角、
邻补角等知识来说明.知2-讲 例4 如图,∠1=65°,∠2=65°,∠3=115°,试
说明(1)DE∥BC; (2)DF∥AB.
根据图形,完成下列推理:
(1)∵∠1=65°,∠2=65°,
∴∠1=∠2.
∴_____∥_____( ).
(2)∵AB,DE相交,∴∠1=∠4( ).
∴∠4=65°,又∵∠3=115°,
∴∠3+∠4=180°,
∴_____∥____( ).
同旁内角互补,两直线平行
DEBC同位角相等,两直线平行对顶角相等DFAB知2-讲∠1与∠2是直线DE,BC被直线AB所截得到的同
位角,所以DE∥BC,理由是“同位角相等,两直
线平行”.∠1与∠4是两条直线AB与DE相交得到
的对顶角,所以∠1=∠4,理由是“对顶角相等”,
∠3与∠4是直线DF,AB被直线DE所截得到的同
旁内角,所以DF∥AB,理由是“同旁内角互补,
两直线平行”.导引:知2-讲(1)由两角相等或互补关系,判定两条直线平行,其
关键是找出两个角是哪两条直线被哪一条直线所
截而成的角.
(2)是选用两角相等,还是选用互补关系说明两直线
平行,应根据实际图形,灵活运用其中一种方法
说明即可.知2-讲判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两
条直线就是平行线.
方法二:如果两条直线都和第三条直线平行,那么这
两条直线也互相平行.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直
线平行.知2-讲 例5 如图,直线MN和直线AB,CD,EF分别交于点
G,H,P,∠1=∠2,
∠2+∠3=180°,试问:
AB与EF平行吗?为什么?
导引:要说明AB∥EF,我们无法找出这两条直线被
MN所截的角相等或互补的条件,因此可考虑这
两条直线是否同时与第三条直线CD平行;即只
需说明AB∥CD,EF∥CD即可.
知2-讲平行.
因为∠1=∠2,∠1=∠BGH,
所以∠2=∠BGH(等量代换),
所以AB∥CD(同位角相等,两直线平行).
所以∠2+∠3=180°,∠3=∠HPF,
所以∠2+∠HPF =180°(等量代换).
所以CD∥EF(同旁内角互补,两直线平行).
所以AB∥EF(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行).解:知2-讲 在判定两条直线互相平行的问题中,如果不能
直接根据平行线的判定方法得出结论,可根据题目
中的已知条件与哪些判定方法的条件相同或相关联,
运用转化思想(用第三条直线作中介)将问题进行转
化(同平行于第三条直线或同垂直于第三条直线),
使之满足平行线的判定方法.知2-练(2015·黔南州)如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
1知2-练(中考·长春)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.15°
B.30°
C.45°
D.60°2知2-练如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
3 1.由“内错角相等”判定两直线平行:内错角相等,
两直线平行.
2.由“同旁内角”判定两直线平行:同旁内角互补,
两直线平行.
“内错角、同旁内角”1课堂讲解由“内错角相等”判定两直线平行、
由“同旁内角互补”判定两直线平行2课时流程逐点
导讲练课堂小结作业提升1知识点由“内错角相等”判定两直线平行知1-讲 两条直线被第三条直线所截,同时得到同位角、
内错角和同旁内角.由同位
角相等,可以判定两条 直
线平行,那么能否利用内
错角来判 定两条直线平
行呢?知1-讲判定方法2 两条直线被第三条直线所截,如果内错
角相等,那么这两条 直线平行.
简单说成:内错角相等,两直线平行.知1-讲 例1 如图,∠AEF=∠EFC,则下列结论中正 确
的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
导引:∠AEF和∠EFC是直线AB,CD被直线EF所截
得到的内错角,根据“内错角相等,两直线平
行”可知,AB∥CD.B知1-讲利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,
看其是否相等.若相等,则两条直线平行.知1-讲 例2 如图,已知∠ADE=60°,DF平分∠ADE,
∠1=30°,试
说明:DF∥BE.
导引:要想说明DF∥BE,可通过说明∠1=∠EDF
来实现,由于∠1=30°,所以只需求出∠EDF
=30°,而这个结论可通过DF是∠ADE的平分
线来求得.知1-讲解:∵DF平分∠ADE(已知),
∴∠EDF= ∠ADE(角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE(内错角相等,两直线平行).知1-讲 要判定两直线平行可以通过说明同位角相等
或内错角相等来实现,至于到底选用同位角还是
选用内错角,要看具体的题目,要尽可能与已知
条件联系.知1-练如图,已知∠1=120°,当∠2=________时,a∥b,理由是________________________________________.1知1-练(2015·福州)下列图形中,由∠1=∠2能得到AB∥CD的是( )
2知1-练如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2 B.∠2=∠3
C.∠3=∠4 D.∠4=∠5
32知识点由“同旁内角互补”判定两直线平行知2-讲探究
遇到一个新问题时,常常把它转化为已知的(或已
解决的)问题. 这一节中,我们是怎样利用“同位角相
等,两直线平行”得到“内错角相 等,两直线平行”
的?你能利用“同位角相等,两直线平行”或“内错
角相等,两直线平行”得到“同旁内角互补,两直线
平行”吗?知2-讲两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
简称:同旁内角互补,两直线平行.?
表达方式:如图:
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两
直线平行).知2-讲 例3 如图,直线AE,CD相交于点O,如果∠A=
110°,∠1=70°,就可以说明AB∥CD,
这是为什么?
?
导引:由题意可知∠1=∠AOD=70°,又∵∠A=
110°,∴∠A+∠AOD=180°,故 AB∥CD.
知2-讲解:因为∠1=∠AOD(对顶角相等),∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).
知2-讲1.本题运用数形结合思想.平行线的判定是由角之间
的数量关系到“形”的判定.要判定两直线平行,可
围绕截线找同位角、内错角或同旁内角,若同位角
相等、内错角相等或同旁内角互补,则两直线平行.
2.用同位角相等、内错角相等或同旁内角互补中的一
个方法说明两直线平行时,一般都要通过结合对顶角、
邻补角等知识来说明.知2-讲 例4 如图,∠1=65°,∠2=65°,∠3=115°,试
说明(1)DE∥BC; (2)DF∥AB.
根据图形,完成下列推理:
(1)∵∠1=65°,∠2=65°,
∴∠1=∠2.
∴_____∥_____( ).
(2)∵AB,DE相交,∴∠1=∠4( ).
∴∠4=65°,又∵∠3=115°,
∴∠3+∠4=180°,
∴_____∥____( ).
同旁内角互补,两直线平行
DEBC同位角相等,两直线平行对顶角相等DFAB知2-讲∠1与∠2是直线DE,BC被直线AB所截得到的同
位角,所以DE∥BC,理由是“同位角相等,两直
线平行”.∠1与∠4是两条直线AB与DE相交得到
的对顶角,所以∠1=∠4,理由是“对顶角相等”,
∠3与∠4是直线DF,AB被直线DE所截得到的同
旁内角,所以DF∥AB,理由是“同旁内角互补,
两直线平行”.导引:知2-讲(1)由两角相等或互补关系,判定两条直线平行,其
关键是找出两个角是哪两条直线被哪一条直线所
截而成的角.
(2)是选用两角相等,还是选用互补关系说明两直线
平行,应根据实际图形,灵活运用其中一种方法
说明即可.知2-讲判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两
条直线就是平行线.
方法二:如果两条直线都和第三条直线平行,那么这
两条直线也互相平行.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直
线平行.知2-讲 例5 如图,直线MN和直线AB,CD,EF分别交于点
G,H,P,∠1=∠2,
∠2+∠3=180°,试问:
AB与EF平行吗?为什么?
导引:要说明AB∥EF,我们无法找出这两条直线被
MN所截的角相等或互补的条件,因此可考虑这
两条直线是否同时与第三条直线CD平行;即只
需说明AB∥CD,EF∥CD即可.
知2-讲平行.
因为∠1=∠2,∠1=∠BGH,
所以∠2=∠BGH(等量代换),
所以AB∥CD(同位角相等,两直线平行).
所以∠2+∠3=180°,∠3=∠HPF,
所以∠2+∠HPF =180°(等量代换).
所以CD∥EF(同旁内角互补,两直线平行).
所以AB∥EF(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行).解:知2-讲 在判定两条直线互相平行的问题中,如果不能
直接根据平行线的判定方法得出结论,可根据题目
中的已知条件与哪些判定方法的条件相同或相关联,
运用转化思想(用第三条直线作中介)将问题进行转
化(同平行于第三条直线或同垂直于第三条直线),
使之满足平行线的判定方法.知2-练(2015·黔南州)如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
1知2-练(中考·长春)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.15°
B.30°
C.45°
D.60°2知2-练如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
3 1.由“内错角相等”判定两直线平行:内错角相等,
两直线平行.
2.由“同旁内角”判定两直线平行:同旁内角互补,
两直线平行.
