5.3.1 平行线的性质课件
图片预览











文档简介
课件30张PPT。第五章 相交线与平行线5.3 平行线的性质第1课时 平行线的性质1课堂讲解“同位角”的性质
“内错角”的性质
“同旁内角”的性质2课时流程逐点
导讲练课堂小结作业提升 利用同位角相等,或者内错角相等,或者同旁内
角互补,可以判定两条直线平行. 反过来,如果两条直
线平行,同位角、内错角、同旁内角又各有什么 关系
呢?这就是我们下面要学习的平行线的性质.
类似于研究平行线的判定,我们先来研究两条直
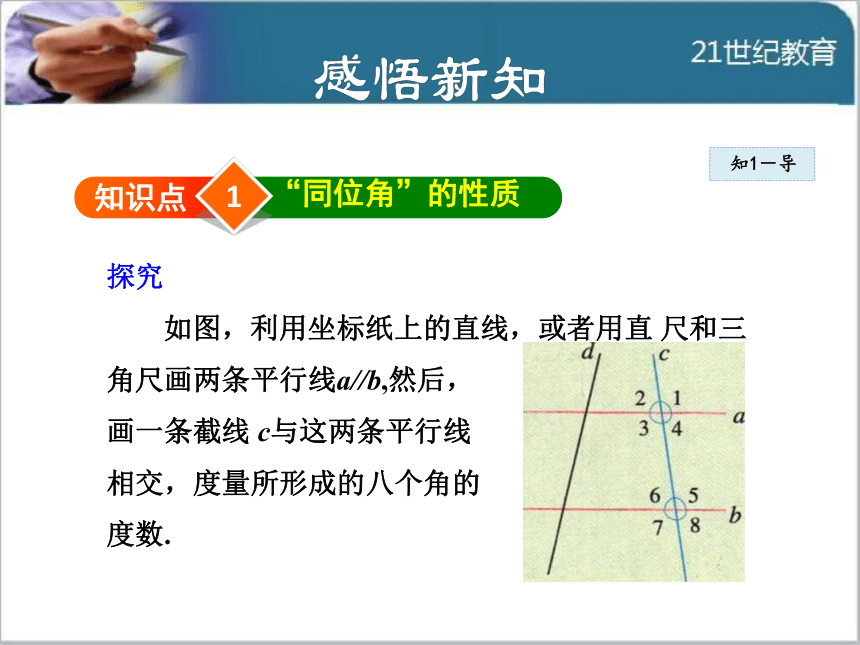
线平行时,它们被第三条直线截得的同位角的关系.1知识点“同位角”的性质探究
如图,利用坐标纸上的直线,或者用直 尺和三
角尺画两条平行线a//b,然后,
画一条截线 c与这两条平行线
相交,度量所形成的八个角的
度数.知1-导 ∠1,∠2,…,∠8中,哪些是同位角?它们 的
度数之间有什么关系?由此猜想两条平行线被第 三
条直线截得的同位角有什么关系.
再任意画一条截线d同样度量并比较各对同 位
角的度数,你的猜想还成立吗?知1-导知1-导 一般地,平行线具有性质:
性质1 两条平行线被第三条直线所截,同位角相等
简单说成:两直线平行,同位角相等. “同位角”的性质:
两条平行线被第三条直线所截,同位角相等.
简称:两直线平行,同位角相等.
表达方式:如图,∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).知1-讲 例1 如图,直线a∥b,直线c与a,b相交,∠1=
70°,则∠2的大小是( )
A.20°
B.50°
C.70°
D.110°
导引:观察图形可以把求∠2转化为求∠2的对顶角
来解,因为∠2的对顶角与∠1是同位角,而
直线a∥b,所以∠2=∠1=70°.知1-讲C知1-讲 有关两直线平行,同位角相等的性质,分清两
个角的位置关系是解答此类题目的关键. 例2 如图,若AB∥CD,且∠1=∠2,试判断AM
与CN的位置关系,并说明
理由.
导引:AM与CN的位置关系很显然
是平行,要说明AM∥CN,
可考虑说明∠EAM=∠ECN. 因为∠1=∠2,
所以只需说明∠BAE=∠ACD即可,由于“两
直线平行,同位角相等”,所以根据 AB∥CD
即可得出∠BAE=∠ACD.知1-讲解:AM∥CN.
理由:∵AB∥CD(已知),
∴∠BAE=∠ACD(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠EAM=∠ECN(等式性质).
∴AM∥CN(同位角相等,两直线平行).知1-讲知1-讲 平行线和角的大小关系是紧密联系在一起的,
由平行线可以得到相等的角,反过来又可以由相等
的角得到新的一组平行线,这种角的大小关系与直
线的位置关系的相互转化在解题中会经常涉及.当
题目已知条件中出现两直线平行时,要考虑是否出
现了相等的角.1(2016·黄冈)如图,直线a∥b,∠1=55°,则∠2=( )
A.35° B.45°
C.55° D.65°
(2015?咸宁)如图,把一块直角三角板的直角顶点
放在直尺的一边上,若∠1=50°,则∠2的度数
为( )
A.50° B.40°
C.30° D.25°知1-练23(2015?随州)如图,AB∥CD,∠A=50°,则∠1
的大小是( )
A.50° B.120°
C.130° D.150°
如图,直线a∥b,∠1=60°,∠2=40°,则∠3
等于( )
A.40° B.60°
C.80° D.100°知1-练42知识点“内错角”的性质知2-导思考
上一节,我们利用“同位角相等,两直线平行”
推出了“内错角相 等,两直线平行”.类似地,你
能由性质1,推出两条平行线被第三条直线截得的
内错角之间的关系吗?知2-导 如图,直线a//b , c是截线. 根据“两 直线平行,
同位角相等”,可得∠2 = ∠3.而∠3 和∠1互为对顶
角,所以∠3 =∠1所以∠1=∠2 .这样,我们就得到
了平行线的另一个性质:
性质2 两条平行线被第三条直
线所截,内错 角相等.
简单说成:两直线平行,
内错角相等.知2-讲表达方式:如图,
因为a∥b(已知),
所以∠1=∠2(两直线平行,内错角相等).知2-讲 例3 如图,MN,EF表示两面互相平行的镜面,一
束光线AB照射到镜面MN上,反射光线为BC,
此时∠1=∠2,光线BC经过镜面EF反射后的
光线为CD,此时∠3=∠4,试判断AB与CD的
位置关系,并说明理由.知2-讲导引:要判断AB与CD的位置关系,应从两直线的
位置关系的特殊情况,如平行或垂直方面
思考问题,观察图可知,AB与CD没有交点,
所以可猜想AB∥CD,要说明AB∥CD,只
要说明∠ABC=∠BCD即可.知2-讲解:AB∥CD,理由如下:
∵MN∥EF,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠2=∠3,∠3=∠4,
∴∠1+∠2=∠3+∠4.
∵∠1+∠ABC+∠2=180°,
∠3+∠BCD+∠4=180°,
∴∠ABC=∠BCD.
∴AB∥CD(内错角相等,两直线平行).知2-讲(1)利用平行线的性质解决实际问题时,其关键是根
据实际问题建立数学模型;
(2)判断两直线的位置关系时,一般都从两直线平行
或垂直这两种特殊情况去思考.1(2016·张家界)如图,将一块直角三角尺的直角顶
点放在直尺的一边上,如果∠1=50°,那么∠2
的度数是( )
A.30° B.40° C.50° D.60°知2-练2(2016·凉山州)如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )
A.26° B.64° C.52° D.128°知2-练3知识点“同旁内角”的性质知3-讲“同旁内角”的性质:
两条平行线被第三条直线所截,同旁内角互补.
简称:两直线平行,同旁内角互补.
表达方式:如图,
因为a∥b(已知),
所以∠1+∠2=180°(两直线平行,同旁内角互补).知3-讲 例4 如图,如果AB∥DF,DE∥BC,且∠1=
65°,那么你能说出∠2,∠3,∠4的度数吗?
为什么?
导引:由DE∥BC,可得∠1=∠4,∠1+∠2=
180°;由DF∥AB,可得∠3=∠2,从而得
∠2,∠3,∠4的度数.知3-讲解:∵DE∥BC(已知),
∴∠4=∠1=65°(两直线平行,内错角相等),
∠2+∠1=180°(两直线平行,同旁内角互补).
∴∠2=180°-∠1=180°-65°=115°.
又∵DF∥AB(已知),
∴∠3=∠2(两直线平行,同位角相等).
∴∠3=115°(等量代换).知3-讲1.求角的度数的基本思路:根据平行线的判定由角的数量
关系得到直线的位置关系,根据平行线的性质由直线的
位置关系得到角的数量关系,通过上述相互转化,从而
找到所求角与已知角之间的关系.
2.两直线平行时,应联想到平行线的三个性质,由两条直
线平行的位置关系得到两个相关角的数量关系,由角的
关系求相应角的度数.1如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=21°,那么∠2=________.知3-练2如图,小明在操场上从A点出发,先沿南偏东30°
方向走到B点,再沿南偏东60°方向走到C点,
这时,∠ABC的度数是( )
A.120°
B.135°
C.150°
D.160°知3-练1.平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
2.平行线的性质与平行线的判定的区别.
判定:角的关系→平行的关系
性质:平行的关系→角的关系
“内错角”的性质
“同旁内角”的性质2课时流程逐点
导讲练课堂小结作业提升 利用同位角相等,或者内错角相等,或者同旁内
角互补,可以判定两条直线平行. 反过来,如果两条直
线平行,同位角、内错角、同旁内角又各有什么 关系
呢?这就是我们下面要学习的平行线的性质.
类似于研究平行线的判定,我们先来研究两条直
线平行时,它们被第三条直线截得的同位角的关系.1知识点“同位角”的性质探究
如图,利用坐标纸上的直线,或者用直 尺和三
角尺画两条平行线a//b,然后,
画一条截线 c与这两条平行线
相交,度量所形成的八个角的
度数.知1-导 ∠1,∠2,…,∠8中,哪些是同位角?它们 的
度数之间有什么关系?由此猜想两条平行线被第 三
条直线截得的同位角有什么关系.
再任意画一条截线d同样度量并比较各对同 位
角的度数,你的猜想还成立吗?知1-导知1-导 一般地,平行线具有性质:
性质1 两条平行线被第三条直线所截,同位角相等
简单说成:两直线平行,同位角相等. “同位角”的性质:
两条平行线被第三条直线所截,同位角相等.
简称:两直线平行,同位角相等.
表达方式:如图,∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).知1-讲 例1 如图,直线a∥b,直线c与a,b相交,∠1=
70°,则∠2的大小是( )
A.20°
B.50°
C.70°
D.110°
导引:观察图形可以把求∠2转化为求∠2的对顶角
来解,因为∠2的对顶角与∠1是同位角,而
直线a∥b,所以∠2=∠1=70°.知1-讲C知1-讲 有关两直线平行,同位角相等的性质,分清两
个角的位置关系是解答此类题目的关键. 例2 如图,若AB∥CD,且∠1=∠2,试判断AM
与CN的位置关系,并说明
理由.
导引:AM与CN的位置关系很显然
是平行,要说明AM∥CN,
可考虑说明∠EAM=∠ECN. 因为∠1=∠2,
所以只需说明∠BAE=∠ACD即可,由于“两
直线平行,同位角相等”,所以根据 AB∥CD
即可得出∠BAE=∠ACD.知1-讲解:AM∥CN.
理由:∵AB∥CD(已知),
∴∠BAE=∠ACD(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠EAM=∠ECN(等式性质).
∴AM∥CN(同位角相等,两直线平行).知1-讲知1-讲 平行线和角的大小关系是紧密联系在一起的,
由平行线可以得到相等的角,反过来又可以由相等
的角得到新的一组平行线,这种角的大小关系与直
线的位置关系的相互转化在解题中会经常涉及.当
题目已知条件中出现两直线平行时,要考虑是否出
现了相等的角.1(2016·黄冈)如图,直线a∥b,∠1=55°,则∠2=( )
A.35° B.45°
C.55° D.65°
(2015?咸宁)如图,把一块直角三角板的直角顶点
放在直尺的一边上,若∠1=50°,则∠2的度数
为( )
A.50° B.40°
C.30° D.25°知1-练23(2015?随州)如图,AB∥CD,∠A=50°,则∠1
的大小是( )
A.50° B.120°
C.130° D.150°
如图,直线a∥b,∠1=60°,∠2=40°,则∠3
等于( )
A.40° B.60°
C.80° D.100°知1-练42知识点“内错角”的性质知2-导思考
上一节,我们利用“同位角相等,两直线平行”
推出了“内错角相 等,两直线平行”.类似地,你
能由性质1,推出两条平行线被第三条直线截得的
内错角之间的关系吗?知2-导 如图,直线a//b , c是截线. 根据“两 直线平行,
同位角相等”,可得∠2 = ∠3.而∠3 和∠1互为对顶
角,所以∠3 =∠1所以∠1=∠2 .这样,我们就得到
了平行线的另一个性质:
性质2 两条平行线被第三条直
线所截,内错 角相等.
简单说成:两直线平行,
内错角相等.知2-讲表达方式:如图,
因为a∥b(已知),
所以∠1=∠2(两直线平行,内错角相等).知2-讲 例3 如图,MN,EF表示两面互相平行的镜面,一
束光线AB照射到镜面MN上,反射光线为BC,
此时∠1=∠2,光线BC经过镜面EF反射后的
光线为CD,此时∠3=∠4,试判断AB与CD的
位置关系,并说明理由.知2-讲导引:要判断AB与CD的位置关系,应从两直线的
位置关系的特殊情况,如平行或垂直方面
思考问题,观察图可知,AB与CD没有交点,
所以可猜想AB∥CD,要说明AB∥CD,只
要说明∠ABC=∠BCD即可.知2-讲解:AB∥CD,理由如下:
∵MN∥EF,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠2=∠3,∠3=∠4,
∴∠1+∠2=∠3+∠4.
∵∠1+∠ABC+∠2=180°,
∠3+∠BCD+∠4=180°,
∴∠ABC=∠BCD.
∴AB∥CD(内错角相等,两直线平行).知2-讲(1)利用平行线的性质解决实际问题时,其关键是根
据实际问题建立数学模型;
(2)判断两直线的位置关系时,一般都从两直线平行
或垂直这两种特殊情况去思考.1(2016·张家界)如图,将一块直角三角尺的直角顶
点放在直尺的一边上,如果∠1=50°,那么∠2
的度数是( )
A.30° B.40° C.50° D.60°知2-练2(2016·凉山州)如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )
A.26° B.64° C.52° D.128°知2-练3知识点“同旁内角”的性质知3-讲“同旁内角”的性质:
两条平行线被第三条直线所截,同旁内角互补.
简称:两直线平行,同旁内角互补.
表达方式:如图,
因为a∥b(已知),
所以∠1+∠2=180°(两直线平行,同旁内角互补).知3-讲 例4 如图,如果AB∥DF,DE∥BC,且∠1=
65°,那么你能说出∠2,∠3,∠4的度数吗?
为什么?
导引:由DE∥BC,可得∠1=∠4,∠1+∠2=
180°;由DF∥AB,可得∠3=∠2,从而得
∠2,∠3,∠4的度数.知3-讲解:∵DE∥BC(已知),
∴∠4=∠1=65°(两直线平行,内错角相等),
∠2+∠1=180°(两直线平行,同旁内角互补).
∴∠2=180°-∠1=180°-65°=115°.
又∵DF∥AB(已知),
∴∠3=∠2(两直线平行,同位角相等).
∴∠3=115°(等量代换).知3-讲1.求角的度数的基本思路:根据平行线的判定由角的数量
关系得到直线的位置关系,根据平行线的性质由直线的
位置关系得到角的数量关系,通过上述相互转化,从而
找到所求角与已知角之间的关系.
2.两直线平行时,应联想到平行线的三个性质,由两条直
线平行的位置关系得到两个相关角的数量关系,由角的
关系求相应角的度数.1如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=21°,那么∠2=________.知3-练2如图,小明在操场上从A点出发,先沿南偏东30°
方向走到B点,再沿南偏东60°方向走到C点,
这时,∠ABC的度数是( )
A.120°
B.135°
C.150°
D.160°知3-练1.平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
2.平行线的性质与平行线的判定的区别.
判定:角的关系→平行的关系
性质:平行的关系→角的关系
