5.3.2 平行线的判定和性质的综合应用课件
文档属性
| 名称 | 5.3.2 平行线的判定和性质的综合应用课件 |  | |
| 格式 | zip | ||
| 文件大小 | 384.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 15:07:32 | ||
图片预览






文档简介
课件28张PPT。第五章 相交线与平行线5.3 平行线的性质第2课时 平行线的判定和性
质的综合应用1课堂讲解平行线的性质的应用
平行线的判定的应用
平行线的性质与判定的综合应用2课时流程逐点
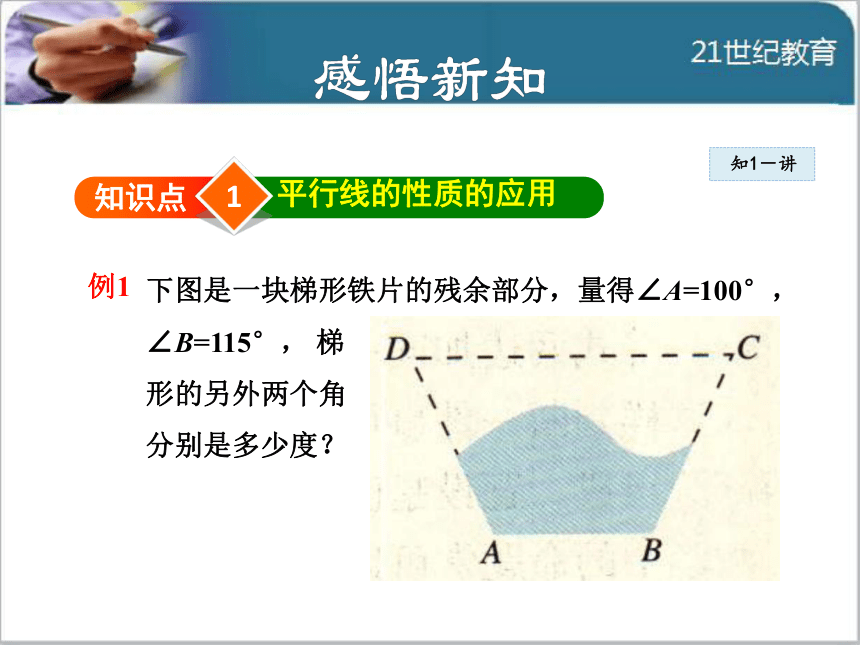
导讲练课堂小结作业提升1知识点平行线的性质的应用下图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°, 梯
形的另外两个角
分别是多少度?知1-讲 例1知1-讲因为梯形上、下两底AB与DC互相平行,
根据“两直线平行,同旁内角互补”,可得∠A与
∠D互补, ∠B与∠C互.补
于是
∠D = 180°-∠A=180°-100°=80°,
∠C = 180°-∠B=180°-115°=65° .
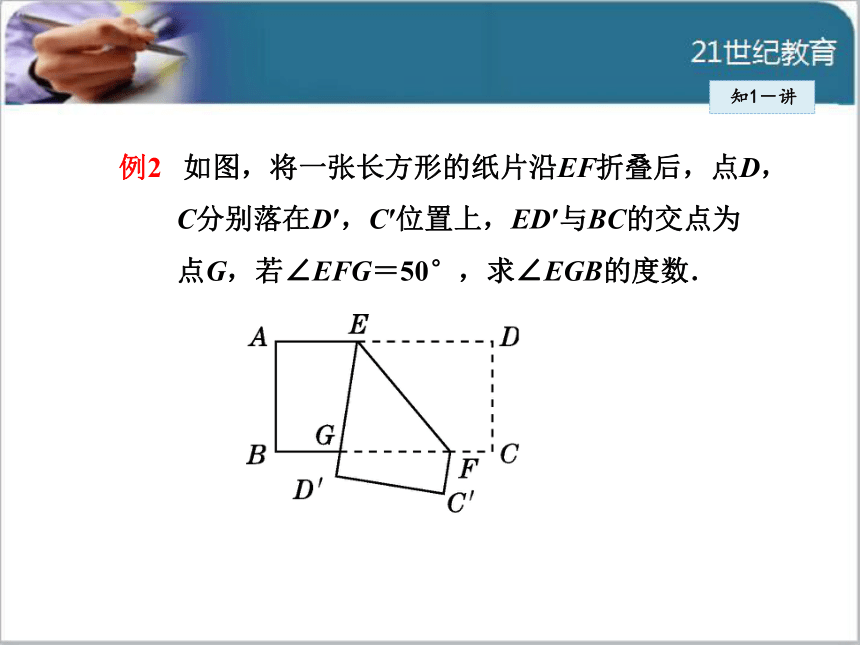
所以梯形的另外两个角分别是80°,65°.解:知1-讲 例2 如图,将一张长方形的纸片沿EF折叠后,点D,
C分别落在D′,C′位置上,ED′与BC的交点为
点G,若∠EFG=50°,求∠EGB的度数.导引:本题根据长方形的对边是平行的,利用平行线
的性质:两直线平行,内错角相等,先求
∠DEF=50°,再根据折叠前后的对应角相等
求得∠D′EF=50°,然后根据平角的定义得
∠AEG=80°,最后根据两直线平行,同旁内
角互补求得∠EGB=100°.
解:∵四边形ABCD是长方形(已知),
∴∠A=∠B=90°(长方形的定义).
∴∠A+∠B=180°,知1-讲∴AD∥BC(同旁内角互补,两直线平行).
∴∠DEF=∠EFG(两直线平行,内错角相等).
∵∠EFG=50°(已知),
∴∠DEF=50°(等量代换).
∵∠DEF=∠D′EF(折叠的性质),
∴∠D′EF=50°(等量代换).
∴∠AEG=180°-∠DEF-∠D′EF=80°(平角的定义).
又∵AD∥BC,
∴∠AEG+∠EGB=180°(两直线平行,同旁内角互补),
∴∠EGB=180°-∠AEG=180°-80°=100°.知1-讲知1-讲 解决折叠问题的关键是找到折叠前后相等的角,
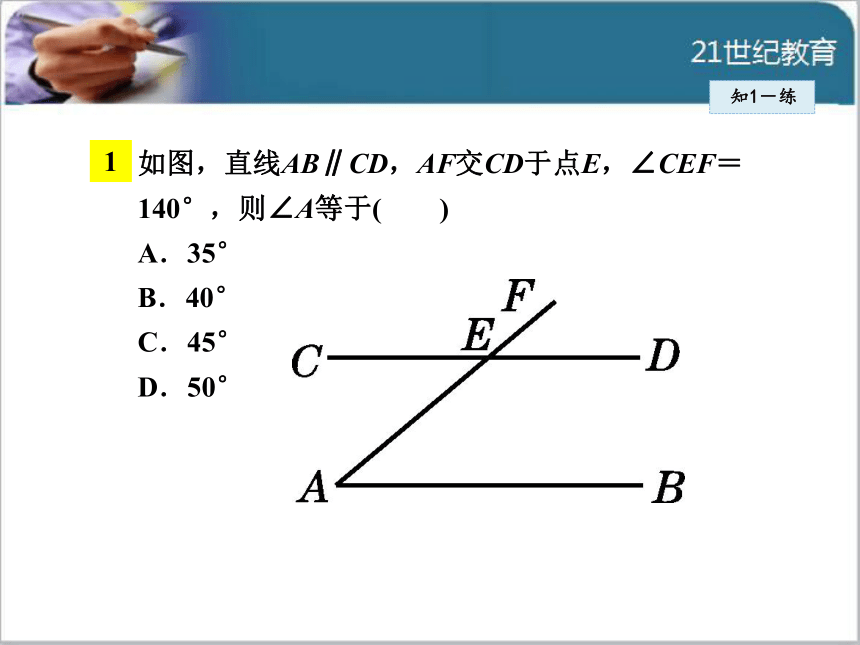
然后熟练利用平行线的性质来求角的度数.1如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
A.35°
B.40°
C.45°
D.50°知1-练2(2015?十堰)如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
A.70° B.60° C.55° D.50°知1-练3(2016·湖州改编)如图是我们生活中经常接触的小刀,刀柄的外形是一个直角梯形(挖去一个半圆形),刀片上、下两边是平行的,转动刀片时形成∠1、∠2,则∠1+∠2=________.知1-练2知识点平行线的判定的应用知2-讲 例3 如图所示,∠B=∠D,∠CEF=∠A.
试问CD与EF平行吗?为什么?知2-讲导引:1.要说明CD∥EF,我们无法找出相等的同位
角、内错角,也无法说明其同旁内角互补,
因此需找第三条直线与它们平行(即AB∥CD,
AB∥EF),这都能由已知∠B=∠D,
∠CEF=∠A说明.
2.由已知∠B=∠D,∠CEF=∠A很容易就能
得出AB∥CD及EF∥AB,再由如果两条直线
都和第三条直线平行,那么这两条直线也互
相平行就可得到CD∥EF.知2-讲解:CD∥EF,理由:
∵∠B=∠D,
∴AB∥CD(内错角相等,两直线平行).
∵∠CEF=∠A,
∴EF∥AB(同位角相等,两直线平行).
∴CD∥EF(平行于同一条直线的两条直线平行).知2-讲找寻说明平行的方法:
1. 分析法:由结论往前推,要说明这个结论成立需要什么样
的条件,一直递推到已知条件为止;(如导引1)
2. 综合法:由已知条件一步一步往后推理,看这个已知条件
能推出什么结论, 一直推导出要说明的结论为止; (如导引2)
3. 两头凑:当遇到复杂问题的时候,我们常常将分析法和综
合法同时进行,即由两头向中间推,寻找到中间的结合点.知2-讲 例4 光线从空气射入水中时,传播方向会发生改变,
这种现象叫做光的折射现象.同样,光线从水
中射入空气中时,也会发生折射现象,一束光
线从空气射入水中再从水中射入空气中时,光
线的传播方向如图,其中,直线a,b都表示空
气与水的分界面.已知∠1=
∠4,∠2=∠3,请你判断光
线c与d是否平行?为什么?知2-讲导引:设光线在水中的部分为e,e与直线a所成的钝
角为∠5,e与直线b所成的钝角为∠6,只要
能说明∠1+∠5=∠4+∠6,则根据“内错
角相等,两直线平行”即可判定c∥d.知2-讲解:c∥d.理由如下:
如图,设光线在水中的部分为e.
∵∠2+∠5=180°,∠3+∠6=180°,
∠2=∠3,
∴∠5=∠6(等角的补角相等).
又∵∠1=∠4,
∴∠1+∠5=∠4+∠6.
∴c∥d(内错角相等,两直线平行).知2-讲 判断光线c与d是否平行,应首先解决两个关键问
题,一是把实物图抽象为“三线八角”的基本图形;
二是把直线c,d看作被直线e所截的两条直线.如此,
问题转化为说明∠1+∠5=∠4+∠6.1如图,已知BE平分∠ABC,CF平分∠BCD,
∠1=∠2,那么直线AB与CD的位置关系是________.知2-练1(2016·菏泽)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°
角的三角板的一个
顶点在纸条的另一
边上,则∠1的度数
是________.知2-练3知识点平行线的性质与判定的综合应用知3-讲平行线的性质与判定之间既有联系又有区别,一定不
可混淆二者的条件和结论,要把它们严格区别开来.知3-讲 例5 如图,已知∠ABC与∠ECB互补,∠1=∠2,
则∠P与∠Q 一定相等吗?说说你的理由.
导引:如果∠P和∠Q相等,那么PB∥
CQ,∴要判断∠P与∠Q是否相
等,只需判断PB和CQ是否平行.
要说明PB∥CQ,可以通过说明
∠PBC=∠BCQ来实现,由于∠1=∠2,因此
只需说明∠ABC=∠BCD即可.知3-讲解:∠P=∠Q.
理由如下:∵∠ABC与∠ECB互补(已知),
∴AB∥ED(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠ABC-∠1=∠BCD-∠2(等式的性质),
即∠PBC=∠BCQ.
∴PB∥CQ(内错角相等,两直线平行).
∴∠P=∠Q(两直线平行,内错角相等).知3-讲 一个数学问题的构成含有四个要素:题目的条
件、解题的依据、解题的方法、题目的结论,如果
题目所含的四个要素解题者已经知道或者结论虽未
指明,但它是完全确定的,这样的问题就是封闭性
的数学问题.1(2015?河南)如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数为( )
A.55°
B.60°
C.70°
D.75°知3-练2如图,如果AB∥DE,∠1=∠2,那么AE∥
DC,请说明理由.知3-练 从图形中得出结论是图形的性质;而从具备
什么条件推理出图形是图形的判定;特别说明,
图形的定义既是图形的判定,也是图形的性质;
即:条件
结论. 图形
质的综合应用1课堂讲解平行线的性质的应用
平行线的判定的应用
平行线的性质与判定的综合应用2课时流程逐点
导讲练课堂小结作业提升1知识点平行线的性质的应用下图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°, 梯
形的另外两个角
分别是多少度?知1-讲 例1知1-讲因为梯形上、下两底AB与DC互相平行,
根据“两直线平行,同旁内角互补”,可得∠A与
∠D互补, ∠B与∠C互.补
于是
∠D = 180°-∠A=180°-100°=80°,
∠C = 180°-∠B=180°-115°=65° .
所以梯形的另外两个角分别是80°,65°.解:知1-讲 例2 如图,将一张长方形的纸片沿EF折叠后,点D,
C分别落在D′,C′位置上,ED′与BC的交点为
点G,若∠EFG=50°,求∠EGB的度数.导引:本题根据长方形的对边是平行的,利用平行线
的性质:两直线平行,内错角相等,先求
∠DEF=50°,再根据折叠前后的对应角相等
求得∠D′EF=50°,然后根据平角的定义得
∠AEG=80°,最后根据两直线平行,同旁内
角互补求得∠EGB=100°.
解:∵四边形ABCD是长方形(已知),
∴∠A=∠B=90°(长方形的定义).
∴∠A+∠B=180°,知1-讲∴AD∥BC(同旁内角互补,两直线平行).
∴∠DEF=∠EFG(两直线平行,内错角相等).
∵∠EFG=50°(已知),
∴∠DEF=50°(等量代换).
∵∠DEF=∠D′EF(折叠的性质),
∴∠D′EF=50°(等量代换).
∴∠AEG=180°-∠DEF-∠D′EF=80°(平角的定义).
又∵AD∥BC,
∴∠AEG+∠EGB=180°(两直线平行,同旁内角互补),
∴∠EGB=180°-∠AEG=180°-80°=100°.知1-讲知1-讲 解决折叠问题的关键是找到折叠前后相等的角,
然后熟练利用平行线的性质来求角的度数.1如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
A.35°
B.40°
C.45°
D.50°知1-练2(2015?十堰)如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
A.70° B.60° C.55° D.50°知1-练3(2016·湖州改编)如图是我们生活中经常接触的小刀,刀柄的外形是一个直角梯形(挖去一个半圆形),刀片上、下两边是平行的,转动刀片时形成∠1、∠2,则∠1+∠2=________.知1-练2知识点平行线的判定的应用知2-讲 例3 如图所示,∠B=∠D,∠CEF=∠A.
试问CD与EF平行吗?为什么?知2-讲导引:1.要说明CD∥EF,我们无法找出相等的同位
角、内错角,也无法说明其同旁内角互补,
因此需找第三条直线与它们平行(即AB∥CD,
AB∥EF),这都能由已知∠B=∠D,
∠CEF=∠A说明.
2.由已知∠B=∠D,∠CEF=∠A很容易就能
得出AB∥CD及EF∥AB,再由如果两条直线
都和第三条直线平行,那么这两条直线也互
相平行就可得到CD∥EF.知2-讲解:CD∥EF,理由:
∵∠B=∠D,
∴AB∥CD(内错角相等,两直线平行).
∵∠CEF=∠A,
∴EF∥AB(同位角相等,两直线平行).
∴CD∥EF(平行于同一条直线的两条直线平行).知2-讲找寻说明平行的方法:
1. 分析法:由结论往前推,要说明这个结论成立需要什么样
的条件,一直递推到已知条件为止;(如导引1)
2. 综合法:由已知条件一步一步往后推理,看这个已知条件
能推出什么结论, 一直推导出要说明的结论为止; (如导引2)
3. 两头凑:当遇到复杂问题的时候,我们常常将分析法和综
合法同时进行,即由两头向中间推,寻找到中间的结合点.知2-讲 例4 光线从空气射入水中时,传播方向会发生改变,
这种现象叫做光的折射现象.同样,光线从水
中射入空气中时,也会发生折射现象,一束光
线从空气射入水中再从水中射入空气中时,光
线的传播方向如图,其中,直线a,b都表示空
气与水的分界面.已知∠1=
∠4,∠2=∠3,请你判断光
线c与d是否平行?为什么?知2-讲导引:设光线在水中的部分为e,e与直线a所成的钝
角为∠5,e与直线b所成的钝角为∠6,只要
能说明∠1+∠5=∠4+∠6,则根据“内错
角相等,两直线平行”即可判定c∥d.知2-讲解:c∥d.理由如下:
如图,设光线在水中的部分为e.
∵∠2+∠5=180°,∠3+∠6=180°,
∠2=∠3,
∴∠5=∠6(等角的补角相等).
又∵∠1=∠4,
∴∠1+∠5=∠4+∠6.
∴c∥d(内错角相等,两直线平行).知2-讲 判断光线c与d是否平行,应首先解决两个关键问
题,一是把实物图抽象为“三线八角”的基本图形;
二是把直线c,d看作被直线e所截的两条直线.如此,
问题转化为说明∠1+∠5=∠4+∠6.1如图,已知BE平分∠ABC,CF平分∠BCD,
∠1=∠2,那么直线AB与CD的位置关系是________.知2-练1(2016·菏泽)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°
角的三角板的一个
顶点在纸条的另一
边上,则∠1的度数
是________.知2-练3知识点平行线的性质与判定的综合应用知3-讲平行线的性质与判定之间既有联系又有区别,一定不
可混淆二者的条件和结论,要把它们严格区别开来.知3-讲 例5 如图,已知∠ABC与∠ECB互补,∠1=∠2,
则∠P与∠Q 一定相等吗?说说你的理由.
导引:如果∠P和∠Q相等,那么PB∥
CQ,∴要判断∠P与∠Q是否相
等,只需判断PB和CQ是否平行.
要说明PB∥CQ,可以通过说明
∠PBC=∠BCQ来实现,由于∠1=∠2,因此
只需说明∠ABC=∠BCD即可.知3-讲解:∠P=∠Q.
理由如下:∵∠ABC与∠ECB互补(已知),
∴AB∥ED(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠ABC-∠1=∠BCD-∠2(等式的性质),
即∠PBC=∠BCQ.
∴PB∥CQ(内错角相等,两直线平行).
∴∠P=∠Q(两直线平行,内错角相等).知3-讲 一个数学问题的构成含有四个要素:题目的条
件、解题的依据、解题的方法、题目的结论,如果
题目所含的四个要素解题者已经知道或者结论虽未
指明,但它是完全确定的,这样的问题就是封闭性
的数学问题.1(2015?河南)如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数为( )
A.55°
B.60°
C.70°
D.75°知3-练2如图,如果AB∥DE,∠1=∠2,那么AE∥
DC,请说明理由.知3-练 从图形中得出结论是图形的性质;而从具备
什么条件推理出图形是图形的判定;特别说明,
图形的定义既是图形的判定,也是图形的性质;
即:条件
结论. 图形
