6.1.1 算术平方根课件
图片预览








文档简介
课件24张PPT。第六章 实数6.1 平方根第1课时 算术平方根1课堂讲解算术平方根的定义
求算术平方根
算术平方根的双重非负性2课时流程逐点
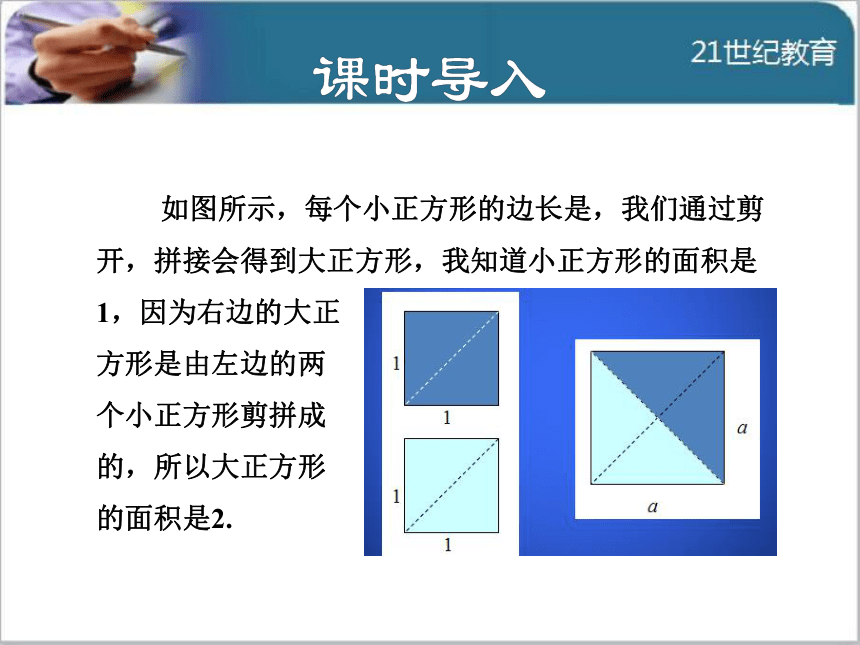
导讲练课堂小结作业提升 如图所示,每个小正方形的边长是,我们通过剪
开,拼接会得到大正方形,我知道小正方形的面积是
1,因为右边的大正
方形是由左边的两
个小正方形剪拼成
的,所以大正方形
的面积是2. 因为正方形的面积是边长乘以边长,所以a2=2,那
么a等于多少呢?我们也就是找一个数,是它的平方
等于2,由于正方形的边长是正数,所以就是找一个
正数,使这个正数的平方等于2,我们把a叫做2的算
术平方根,如果一个正数x的平方等于a,即x2=a,那
么这个正数x就叫做a的算术平方根.1知识点算术平方根的定义问题1:正数3的平方等于9,若x2=9,则正数x=____.
正数4的平方等于16,若x2=16,则正数x=____.
说说6和36这两个数又怎样的关系呢?
问题2:(1) 0的平方是___,如果x2=0,那么x=____.
(2) 0的算术平方根是___.知1-导问题3:学校要举行美术作品比赛,小鸥想裁出一块
面积为25 dm2的正方形画布,画上自己的得
意之作参加比赛,这块正方形画布的边长应
取多少?
你一定会算出边长应取5 dm. 说
一说,你是怎样算出来的?
因为52=25,所以这个正方形画
布的边长应取5 dm. 知1-导填表:
上面的问题,实际上是已知一个正数的平方,求这个
正数的问题.知1-导 一般地,如果一个正数x的平方等于a,即:x2=a,
那么这个正数x叫做a的算术平方根(arithmetic square
root) . a的算术平方根记为 ,读作“根号a”,a叫
做被开方数(radicand).
规定:0的算术平方根是0.知1-导知1-讲下列说法正确的是( )
A.3是9的算术平方根
B.-2是4的算术平方根
C. (-2)2的算术平方根是-2
D.-9的算术平方根是3例1 A知1-讲导引:要正确把握算术平方根的定义.因为3的平方等
于9,所以3是9的算术平方根;因为-2不是正
数,所以-2不是4的算术平方根;因为(-2)2
=4,而22=4,所以2是(-2)2的算术平方根;
负数没有算术平方根.知1-讲 算术平方根具有双重非负性:这个数是非负数,
它的算术平方根也是非负数.知1-练1下列说法正确的是( )
A.-1是(-1)2的算术平方根
B.3是-9的算术平方根
C.-1的算术平方根是它本身
D. 的算术平方根是2知1-练2算术平方根等于它本身的数是__________;________的算术平方根等于它的相反数.
(2016·黄冈) 的算术平方根是________.32知识点求算术平方根(1) 正数的算术平方根是一个正数;
(2) 0的算术平方根是0;
(3) 负数没有算术平方根;
(4) 被开方数越大,对应的算术平方根也越大.知2-讲知2-讲求下列各数的算术平方根:
(1) 100; (2) ; (3) 0.0001.例2 解:(1)因为102 = 100,所以100的算术平方根是10,
即
(2)因为( )2 = ,所以 的算术平方根是 ,
即 ;
(3)因为0.012 =0.0001,所以0.0001的算术平方
根是0.01,即 =0.01.知2-讲(1)求一个数的算术平方根时,首先要弄清是求哪个数
的算术平方根,分清求 与81的算术平方根的不
同意义,不要被表面现象迷惑.
(2)求一个非负数的算术平方根常借助于平方运算,因
此熟记常用平方数对求一个数的算术平方根十分有
用.知2-练1求下列各数的算术平方根:
(1) 0.0025; (2) 81; (3) 32.
(2016·杭州) =( )
A.2 B.3 C.4 D.5
设 =a,则下列结论正确的是( )
A.a=441 B.a=4412
C.a=-21 D.a=21233知识点算术平方根的双重非负性问题1: (1)因为_____2=64,所以64的算术平方根是
______,即 =______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,
即 =______.
(3)因为_____2=0,所以0的算术平方根是______,
即 =______.8880.50.50.5000问题2: 讨论:在 中,被开方数a是一个______数,
算术平方根 是一个______数.非负非负知3-导所以算术平方根 具有双重非负性:
1. 被开方数a是非负数,即a ≥0;
2. 算术平方根 本身是非负数,即知3-导知3-讲若 =0,求x2 015+y2 016的值.例3 导引:非负数与非负数的和为0当且仅当这两个非负数
为0时成立,可列方程求出x,y的值,从而求出
代数式的值.
∵ ≥0, ≥0, =0,
∴x-1=0,y+1=0,∴x=1,y=-1.
∴x2 015+y2 016=12 015+(-1)2 016=2.
解:知3-讲 算术平方根和绝对值一样,都是非负数,当
几个非负数的和等于0时,其中每一个非负数都
为0.1已知a,b是有理数,且满足 +|b-2|=0,解关于x的方程(a+2)x+b2=a-1.
(1) 中,被开方数a是_______,即a_______0;
(2) 是________,即 ________0,即非负数的
算术平方根是_______;负数没有算术平方根,
即当a________0时, 无意义.知3-练2知3-练3设a-2是一个数的算术平方根,那么( )
A.a≥0 B.a>0
C.a>2 D.a≥2通过这节课的学习,我们要掌握以下的内容:
(1)算术平方根的概念,式子 中的双重非负性:
一是a≥0,二是 ≥0.
(2)算术平方根的性质:一个正数的算术平方根是一个
正数;0的算术平方根是0;负数没有算术平方根.
(3)求一个正数的算术平方根的运算与平方运算是互逆
的运算,利用这个互逆运算关系求非负数的算术平
方根.
求算术平方根
算术平方根的双重非负性2课时流程逐点
导讲练课堂小结作业提升 如图所示,每个小正方形的边长是,我们通过剪
开,拼接会得到大正方形,我知道小正方形的面积是
1,因为右边的大正
方形是由左边的两
个小正方形剪拼成
的,所以大正方形
的面积是2. 因为正方形的面积是边长乘以边长,所以a2=2,那
么a等于多少呢?我们也就是找一个数,是它的平方
等于2,由于正方形的边长是正数,所以就是找一个
正数,使这个正数的平方等于2,我们把a叫做2的算
术平方根,如果一个正数x的平方等于a,即x2=a,那
么这个正数x就叫做a的算术平方根.1知识点算术平方根的定义问题1:正数3的平方等于9,若x2=9,则正数x=____.
正数4的平方等于16,若x2=16,则正数x=____.
说说6和36这两个数又怎样的关系呢?
问题2:(1) 0的平方是___,如果x2=0,那么x=____.
(2) 0的算术平方根是___.知1-导问题3:学校要举行美术作品比赛,小鸥想裁出一块
面积为25 dm2的正方形画布,画上自己的得
意之作参加比赛,这块正方形画布的边长应
取多少?
你一定会算出边长应取5 dm. 说
一说,你是怎样算出来的?
因为52=25,所以这个正方形画
布的边长应取5 dm. 知1-导填表:
上面的问题,实际上是已知一个正数的平方,求这个
正数的问题.知1-导 一般地,如果一个正数x的平方等于a,即:x2=a,
那么这个正数x叫做a的算术平方根(arithmetic square
root) . a的算术平方根记为 ,读作“根号a”,a叫
做被开方数(radicand).
规定:0的算术平方根是0.知1-导知1-讲下列说法正确的是( )
A.3是9的算术平方根
B.-2是4的算术平方根
C. (-2)2的算术平方根是-2
D.-9的算术平方根是3例1 A知1-讲导引:要正确把握算术平方根的定义.因为3的平方等
于9,所以3是9的算术平方根;因为-2不是正
数,所以-2不是4的算术平方根;因为(-2)2
=4,而22=4,所以2是(-2)2的算术平方根;
负数没有算术平方根.知1-讲 算术平方根具有双重非负性:这个数是非负数,
它的算术平方根也是非负数.知1-练1下列说法正确的是( )
A.-1是(-1)2的算术平方根
B.3是-9的算术平方根
C.-1的算术平方根是它本身
D. 的算术平方根是2知1-练2算术平方根等于它本身的数是__________;________的算术平方根等于它的相反数.
(2016·黄冈) 的算术平方根是________.32知识点求算术平方根(1) 正数的算术平方根是一个正数;
(2) 0的算术平方根是0;
(3) 负数没有算术平方根;
(4) 被开方数越大,对应的算术平方根也越大.知2-讲知2-讲求下列各数的算术平方根:
(1) 100; (2) ; (3) 0.0001.例2 解:(1)因为102 = 100,所以100的算术平方根是10,
即
(2)因为( )2 = ,所以 的算术平方根是 ,
即 ;
(3)因为0.012 =0.0001,所以0.0001的算术平方
根是0.01,即 =0.01.知2-讲(1)求一个数的算术平方根时,首先要弄清是求哪个数
的算术平方根,分清求 与81的算术平方根的不
同意义,不要被表面现象迷惑.
(2)求一个非负数的算术平方根常借助于平方运算,因
此熟记常用平方数对求一个数的算术平方根十分有
用.知2-练1求下列各数的算术平方根:
(1) 0.0025; (2) 81; (3) 32.
(2016·杭州) =( )
A.2 B.3 C.4 D.5
设 =a,则下列结论正确的是( )
A.a=441 B.a=4412
C.a=-21 D.a=21233知识点算术平方根的双重非负性问题1: (1)因为_____2=64,所以64的算术平方根是
______,即 =______.
(2)因为_____2=0.25,所以0.25的算术平方根是______,
即 =______.
(3)因为_____2=0,所以0的算术平方根是______,
即 =______.8880.50.50.5000问题2: 讨论:在 中,被开方数a是一个______数,
算术平方根 是一个______数.非负非负知3-导所以算术平方根 具有双重非负性:
1. 被开方数a是非负数,即a ≥0;
2. 算术平方根 本身是非负数,即知3-导知3-讲若 =0,求x2 015+y2 016的值.例3 导引:非负数与非负数的和为0当且仅当这两个非负数
为0时成立,可列方程求出x,y的值,从而求出
代数式的值.
∵ ≥0, ≥0, =0,
∴x-1=0,y+1=0,∴x=1,y=-1.
∴x2 015+y2 016=12 015+(-1)2 016=2.
解:知3-讲 算术平方根和绝对值一样,都是非负数,当
几个非负数的和等于0时,其中每一个非负数都
为0.1已知a,b是有理数,且满足 +|b-2|=0,解关于x的方程(a+2)x+b2=a-1.
(1) 中,被开方数a是_______,即a_______0;
(2) 是________,即 ________0,即非负数的
算术平方根是_______;负数没有算术平方根,
即当a________0时, 无意义.知3-练2知3-练3设a-2是一个数的算术平方根,那么( )
A.a≥0 B.a>0
C.a>2 D.a≥2通过这节课的学习,我们要掌握以下的内容:
(1)算术平方根的概念,式子 中的双重非负性:
一是a≥0,二是 ≥0.
(2)算术平方根的性质:一个正数的算术平方根是一个
正数;0的算术平方根是0;负数没有算术平方根.
(3)求一个正数的算术平方根的运算与平方运算是互逆
的运算,利用这个互逆运算关系求非负数的算术平
方根.
