6.3.2 实数与数轴的关系及实数的运算课件
文档属性
| 名称 | 6.3.2 实数与数轴的关系及实数的运算课件 |  | |
| 格式 | zip | ||
| 文件大小 | 622.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 15:23:54 | ||
图片预览









文档简介
课件30张PPT。第六章 实数6.3 实数第2课时 实数与数轴的关系
及实数的运算1课堂讲解实数与数轴上的点的关系
实数的大小比较
实数的运算2课时流程逐点
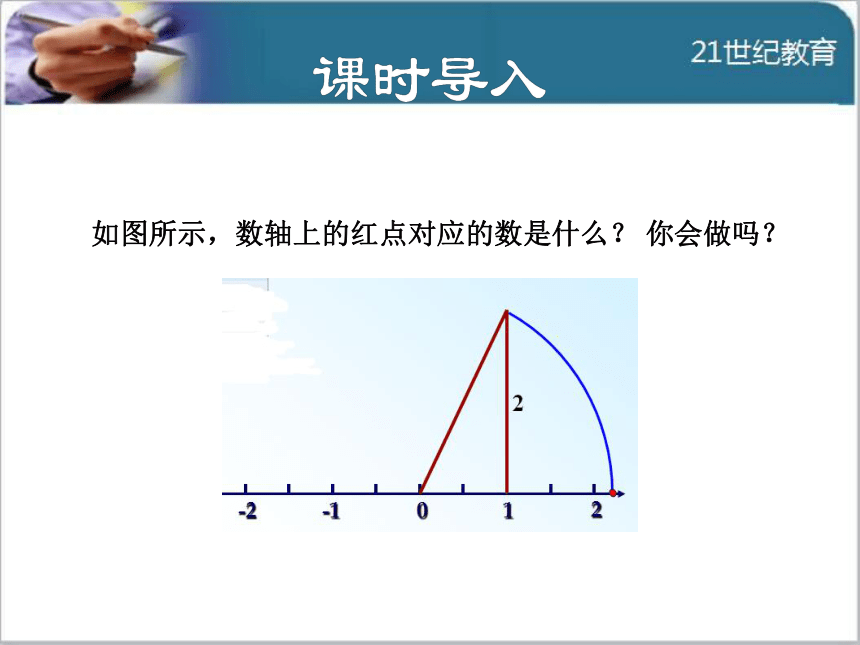
导讲练课堂小结作业提升如图所示,数轴上的红点对应的数是什么? 你会做吗? 1知识点实数与数轴上点的关系探究
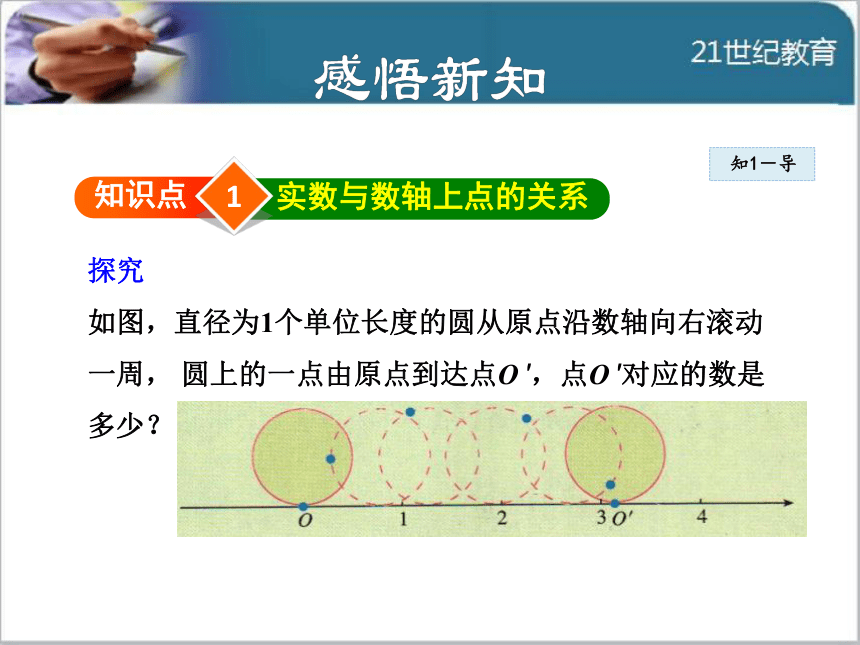
如图,直径为1个单位长度的圆从原点沿数轴向右滚动
一周, 圆上的一点由原点到达点O ′,点O ′对应的数是
多少?知1-导 从图中可以看出, OO ′的长是这个圆的周长π,
所以点O ′对应的数是π. 这样,无理数π可以用数轴上
的点表示出来.知1-导 我们已经知道,每一个有理数都可以用数轴上的
点表示出来.例如,可把-2,-0.5, 和2表示在数轴
上(如图).
那么,数轴上的每一个点都表示一个有理数吗?
答案是否定的.知1-讲 如图,通过画图中正方形ABCD的边长,就能准
确地把 和 表示在数轴上.
在实数范围内,每一个实数都可以用数轴上的点
来表示;反过来,数轴上的每一个点都表示一个实数.
我们说实数和数轴上的点一一对应.知1-讲 在实数范围内,每一个实数都可以用数轴上的点
来表示;反过来,数轴上的每一个点都表示一个实数.
我们说实数和数轴上的点一一对应.知1-讲点A在数轴上表示的数为3 ,点B在数轴上表示的数为-5,则A,B两点之间的距离为________.知1-讲例1 导引:根据数轴上两点间的距离等于右边的点表示的数
减去左边的点表示的数,列式计算即可得解.知1-讲 数轴上两点间的距离的求法:数轴上两点间的
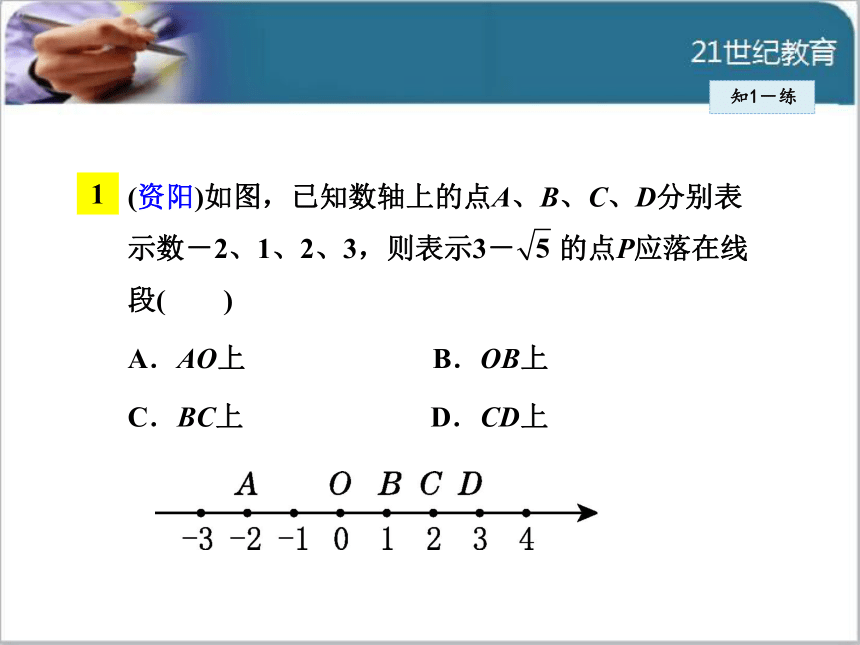
距离等于这两点表示的数之差的绝对值.知1-练1(资阳)如图,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示3- 的点P应落在线段( )
A.AO上 B.OB上
C.BC上 D.CD上知1-练2和数轴上的点一一对应的数是( )
A.整数 B.有理数
C.无理数 D.实数
(2016·金华)若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )
A.a<0 B.ab<0
C.a为在数轴上表示的数,右边的数总比左边的数大. 因
为在数轴上3在2的右边,所以3>2,-2在-3的右边,所
以-2___-3;因为在数轴上 在 的右边,所以
____ ,- 在- 的右边,所以- ____- ,
同理:0____- ,- ____- .
结论:在实数范围内,在数轴上表示的数,右边的数
总比左边的数大.知2-讲>>>>>知2-讲用“<”连接下列各数:- , ,-2 ,2.5,0.例2 导引:比较一组实数的大小和比较一组有理数的大小
一样,可先求出这些数的近似数,再将这些数
在数轴上表示出来,然后根据“在数轴上右边
的点表示的数总比左边的点表示的数大”求解.知2-讲解:将各数的大致位置在数轴上表示出来,如图所
示.
由图可知,各数用“<”可以连接成:-2
<- <0< <2.5.知2-讲 根据“实数与数轴上的点是一一对应的”,并且
“在数轴上右边的点表示的数总比左边的点表示的数
大”,我们可以利用数形结合思想比较实数的大小.知2-练1实数a在数轴上对应的点的位置如图所示,则a,-a,1的大小关系正确的是( )
A.-a<a<1
B.a<-a<1
C.1<-a<a
D.a<1<-a知2-练2(2016·江西)下列四个数中,最大的一个数是( )
A.2 B.
C.0 D.-2
(2016·泰安)如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )
A.p B.q
C.m D.n33知识点实数的运算1. 在实数范围内,进行加、减、乘、除、乘方和开方运算
时,有理数的运算法则和运算律仍然适用;实数混合运
算的运算顺序与有理数的混合运算顺序一样,即先算乘
方、开方,再算乘除,最后算加减,同级运算按照自左
向右的顺序进行,有括号先算括号里面的.
2. 有理数的运算律在实数范围内仍然适用,在进行实数运
算的过程中,要做到:一“看”——看算式的结构特点,
能否运用运算律或公式;二“用”——运用运算律或公
式;三“查”——检查过程和结果是否正确.知3-讲3. 实数的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:ab=ba;
乘法结合律:(ab)c=a(bc);
乘法分配律:(a+b)c=ac+bc.
4. 要点精析:在实数范围内做开方运算时,要注意正
实数和零既能开平方,也能开立方;负实数不能开
平方.知3-讲知3-讲 实数之间不仅可以进行加、减、乘、除(除数不
为0)、乘方运算,而且正数及0可以进行开平方运算,
任意一个实数可以进行开立方运算. 在进行实数的运
算时,有理数的运算法则及运算性质等同样适用.知3-讲计算下列各式的值:
(1) ; (2) .例3 (1)
(2)
解:(加法结合律)(分配律)知3-讲 计算结果如果包含开方开不尽的数,要保留根号.知3-讲计算(结果保留小数点后两位):
(1) ; (2) .例4 (1)
(2)解:知3-讲 实数的运算顺序同有理数的运算顺序.实数运算
中,无理数可选取近似值转化为有理数计算,中间结
果所取的近似值要比结果要求的多一位小数.1计算:
(1)
(2)
(3)知3-练2计算:
(1)
(2) (结果精确到0.01).知3-练1. 当数的范围从有理数扩充到实数后,有理数中关于
相反数、倒数和绝对值的相关性质同样适用于实数.
2. 实数与数轴上的点是一一对应的. 即每一个实数都
可以用数轴上一个点来表示. 反过来数轴上的任何
一个点都表示一个实数. 实数运算时要先确定运算符号及顺序,再进行运
算,运算过程中要熟练运用运算律及各种运算法则,
掌握一定的运算技巧,同时要明确除开偶次方外,其
他各种运算在实数范围内都能实施,且运算结果是唯
一的;开偶次方只有在非负实数范围内才能实施,且
正数的偶次方根有两个.运算种类:
易错警示: (1)负实数只能开奇次方,不能开偶次方;
(2)计算结果中如果包含开方开不尽的数,则保留根号,
结果要化为最简形式.
及实数的运算1课堂讲解实数与数轴上的点的关系
实数的大小比较
实数的运算2课时流程逐点
导讲练课堂小结作业提升如图所示,数轴上的红点对应的数是什么? 你会做吗? 1知识点实数与数轴上点的关系探究
如图,直径为1个单位长度的圆从原点沿数轴向右滚动
一周, 圆上的一点由原点到达点O ′,点O ′对应的数是
多少?知1-导 从图中可以看出, OO ′的长是这个圆的周长π,
所以点O ′对应的数是π. 这样,无理数π可以用数轴上
的点表示出来.知1-导 我们已经知道,每一个有理数都可以用数轴上的
点表示出来.例如,可把-2,-0.5, 和2表示在数轴
上(如图).
那么,数轴上的每一个点都表示一个有理数吗?
答案是否定的.知1-讲 如图,通过画图中正方形ABCD的边长,就能准
确地把 和 表示在数轴上.
在实数范围内,每一个实数都可以用数轴上的点
来表示;反过来,数轴上的每一个点都表示一个实数.
我们说实数和数轴上的点一一对应.知1-讲 在实数范围内,每一个实数都可以用数轴上的点
来表示;反过来,数轴上的每一个点都表示一个实数.
我们说实数和数轴上的点一一对应.知1-讲点A在数轴上表示的数为3 ,点B在数轴上表示的数为-5,则A,B两点之间的距离为________.知1-讲例1 导引:根据数轴上两点间的距离等于右边的点表示的数
减去左边的点表示的数,列式计算即可得解.知1-讲 数轴上两点间的距离的求法:数轴上两点间的
距离等于这两点表示的数之差的绝对值.知1-练1(资阳)如图,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示3- 的点P应落在线段( )
A.AO上 B.OB上
C.BC上 D.CD上知1-练2和数轴上的点一一对应的数是( )
A.整数 B.有理数
C.无理数 D.实数
(2016·金华)若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )
A.a<0 B.ab<0
C.a为在数轴上表示的数,右边的数总比左边的数大. 因
为在数轴上3在2的右边,所以3>2,-2在-3的右边,所
以-2___-3;因为在数轴上 在 的右边,所以
____ ,- 在- 的右边,所以- ____- ,
同理:0____- ,- ____- .
结论:在实数范围内,在数轴上表示的数,右边的数
总比左边的数大.知2-讲>>>>>知2-讲用“<”连接下列各数:- , ,-2 ,2.5,0.例2 导引:比较一组实数的大小和比较一组有理数的大小
一样,可先求出这些数的近似数,再将这些数
在数轴上表示出来,然后根据“在数轴上右边
的点表示的数总比左边的点表示的数大”求解.知2-讲解:将各数的大致位置在数轴上表示出来,如图所
示.
由图可知,各数用“<”可以连接成:-2
<- <0< <2.5.知2-讲 根据“实数与数轴上的点是一一对应的”,并且
“在数轴上右边的点表示的数总比左边的点表示的数
大”,我们可以利用数形结合思想比较实数的大小.知2-练1实数a在数轴上对应的点的位置如图所示,则a,-a,1的大小关系正确的是( )
A.-a<a<1
B.a<-a<1
C.1<-a<a
D.a<1<-a知2-练2(2016·江西)下列四个数中,最大的一个数是( )
A.2 B.
C.0 D.-2
(2016·泰安)如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )
A.p B.q
C.m D.n33知识点实数的运算1. 在实数范围内,进行加、减、乘、除、乘方和开方运算
时,有理数的运算法则和运算律仍然适用;实数混合运
算的运算顺序与有理数的混合运算顺序一样,即先算乘
方、开方,再算乘除,最后算加减,同级运算按照自左
向右的顺序进行,有括号先算括号里面的.
2. 有理数的运算律在实数范围内仍然适用,在进行实数运
算的过程中,要做到:一“看”——看算式的结构特点,
能否运用运算律或公式;二“用”——运用运算律或公
式;三“查”——检查过程和结果是否正确.知3-讲3. 实数的运算律
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:ab=ba;
乘法结合律:(ab)c=a(bc);
乘法分配律:(a+b)c=ac+bc.
4. 要点精析:在实数范围内做开方运算时,要注意正
实数和零既能开平方,也能开立方;负实数不能开
平方.知3-讲知3-讲 实数之间不仅可以进行加、减、乘、除(除数不
为0)、乘方运算,而且正数及0可以进行开平方运算,
任意一个实数可以进行开立方运算. 在进行实数的运
算时,有理数的运算法则及运算性质等同样适用.知3-讲计算下列各式的值:
(1) ; (2) .例3 (1)
(2)
解:(加法结合律)(分配律)知3-讲 计算结果如果包含开方开不尽的数,要保留根号.知3-讲计算(结果保留小数点后两位):
(1) ; (2) .例4 (1)
(2)解:知3-讲 实数的运算顺序同有理数的运算顺序.实数运算
中,无理数可选取近似值转化为有理数计算,中间结
果所取的近似值要比结果要求的多一位小数.1计算:
(1)
(2)
(3)知3-练2计算:
(1)
(2) (结果精确到0.01).知3-练1. 当数的范围从有理数扩充到实数后,有理数中关于
相反数、倒数和绝对值的相关性质同样适用于实数.
2. 实数与数轴上的点是一一对应的. 即每一个实数都
可以用数轴上一个点来表示. 反过来数轴上的任何
一个点都表示一个实数. 实数运算时要先确定运算符号及顺序,再进行运
算,运算过程中要熟练运用运算律及各种运算法则,
掌握一定的运算技巧,同时要明确除开偶次方外,其
他各种运算在实数范围内都能实施,且运算结果是唯
一的;开偶次方只有在非负实数范围内才能实施,且
正数的偶次方根有两个.运算种类:
易错警示: (1)负实数只能开奇次方,不能开偶次方;
(2)计算结果中如果包含开方开不尽的数,则保留根号,
结果要化为最简形式.
