7.1.2 平面直角坐标系课件
图片预览











文档简介
课件30张PPT。第七章 平面直角坐标系7.1 平面直角坐标系第2课时 平面直角坐
标系1课堂讲解平面直角坐标系
各象限内、坐标轴上点的坐标特征特殊点的坐标的特征2课时流程逐点
导讲练课堂小结作业提升 笛卡尔(1596-1660) ,法国数学家、科学家和哲学
家. 早在1637年以前,他受到了经纬度的启发. (地理
上的经纬度是以赤道和本初子午线为标准的,这两条
线从局部上看可以看成平面内互相
垂直的两条线. )发明了平面直角坐
标系,又称笛卡尔坐标系.那么什么
是平面直角坐标系呢?我们今天就
来探讨一下,请随我进入今天的知
识博物馆参观参观!1知识点平面直角坐标系 下图是一条数轴,数轴上的点与实数是一一对应
的. 数轴上每个点都 对应一个实数,这个实数叫做这
个点在数轴上的坐标. 例如,点A在数轴上 的坐标为
-4,点B在数轴上的坐标为2. 反过来,知道数轴上一
个点的坐标, 这个点在数轴上的位置也就确定了. 例
如,数轴上坐标为5的点是点C.知1-导知1-导 类似于利用数轴确定直线上点的位置,能不能找
到一种办法来确定平面内的点的位置呢(例如图中A,
B,C,D各点)?知1-讲1. 坐标:数轴上的点可以用一个实数来表示,这个实
数叫做这个点在数轴上的坐标.
2. 平面直角坐标系:(1)定义:在平面内画两条互相垂
直、原点重合的数轴,组成平面直角坐标系.
(2)相关概念:水平的数轴称为x轴或横轴,习惯上取
向右为正方向;竖直的数轴称为y轴或纵轴,取向
上为正方向;两个坐标轴的交点为平面直角坐标系
的原点.知1-讲要点精析:
(1)一般情况下,平面直角坐标系的两条坐标轴的单位
长度是一致的;但在实际问题中,受两轴表示的实
际意义的影响,两坐标轴的单位长度可以有所不同.
(2) 4个半轴根据实际问题的需要,可画得长些或短些,
但原点必须画出.知1-讲下列语句不正确的是( )
A.平面直角坐标系中,两条互相垂直的数轴的交点是原点
B.平面直角坐标系所在的平面叫坐标平面
C.平面直角坐标系中x轴、y轴把坐标平面分成4部分
D.凡是两条互相垂直的直线都能组成平面直角坐标系例1 D知1-讲导引:本题主要考查平面直角坐标系的概念.根据平
面直角坐标系的概念可知A,B,C项正确.D
项不正确,因为平面直角坐标系必须由数轴构
成,且构成平面直角坐标系的两条数轴互相垂
直、原点重合.知1-讲 本题应用定义法,要正确理解平面直角坐标系的
概念.
理解并认识平面直角坐标系必须明确:(1)建立平
面直角坐标系的平面叫坐标平面;(2)平面直角坐标系
必须具备:①由两条数轴组成;②这两条数轴有公共
原点且互相垂直.知1-练1下列说法错误的是( )
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
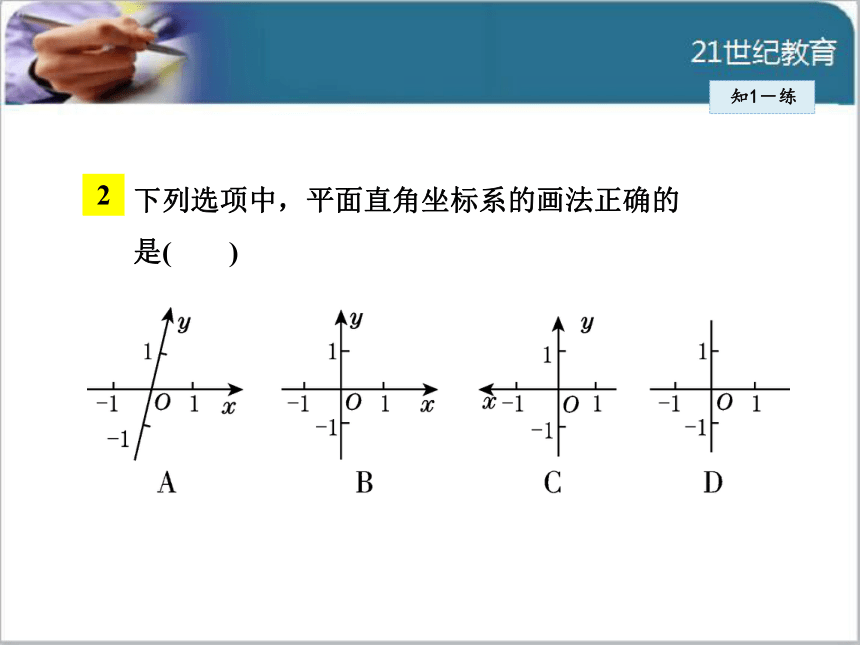
D.坐标轴上的点不属于任何象限知1-练2下列选项中,平面直角坐标系的画法正确的
是( )2知识点各象限内、坐标轴上点的坐标特征知2-导 有了平面直角坐标系,
平面内的点就可以用一个
有序数对来表示了. 例如,
如图,由点A分别向x轴和
y轴作垂线,垂足M在x轴
上的坐标是3,垂足N在y
轴上的坐标是 4,我们说知2-导点A的横坐标是3,纵坐标是4,有序数对(3, 4)就叫做
点A的坐标 (coordinate),记作A(3,4). 类似地,请你
写出点B,C,D的坐标: B(__,__), C(__ ,__),
D(__,__) .建立了平面直角坐标系以后,坐标平面就被两条坐标
轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分(如图),每个部分称
为象限(quadrant),分别
叫做第一象限、 第二象
限、第三象限和第四象
限.坐标轴上的点不属于
任何象限.知2-导知2-讲1. 象限的划分:如图,建立平面直角坐标系后,平
面被坐标轴分成四部分,分别叫第一象限、第二
象限、第三象限、第四象限,坐标轴上的点不属
于任何象限.知2-讲2.平面直角坐标系中各区域的点的坐标的特征:知2-讲例在平面直角坐标系(如图)中描出下列各点:
A(4,5),
B(-2,3),
C(-4,-1),
D(2.5,-2),
E(0,-4).例2 知2-讲解:如图,先在x轴上找出表示4的点,再在y轴上找出
表示5的点,过这两个点分别作x轴和y轴的垂线,
垂线的交点就是点A.
类似地,请你在图上
描出点B,C,D,E.知2-讲 由点的坐标确定点的位置的方法:方法一是由点
的坐标的符号确定点的位置,即(+,+)的点在第一
象限,(-,+)的点在第二象限,(-,-)的点在第三
象限,(+,-)的点在第四象限;方法二是分别过两
坐标轴上表示该点的坐标的点作两坐标轴的垂线,这
两条垂线的交点位置即为该点的位置.知2-练1写出图中点A,B,C,D,E,F的坐标.
知2-练2在图中描出下列各点:
L(-5,-3),M(4, 0),N(-6, 2),P(5,-3.5),
O(0,5),R(6,2).
(2016·广东)在平面直角坐标系中,点P(-2,-3)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限3知2-练4如图,小手盖住的点的坐标可能为( )
A.(5,2) B.(-6,3)
C.(-4,-6) D.(3,-4)3知识点特殊点的坐标的特征知3-导思考
原点O的坐标是什么? x轴和y轴上的点的坐标有什么
特点?
可以看出,原点O的坐标为(0,0);
x轴上的点的纵坐标为0,例如(1,0), (-1,0),…;
y轴上的点的横坐标为0,例如(0,1),(0,-1),… .
知3-导知3-讲导引:根据点在y轴上的特征:横坐标为0,可求出x的
值,然后再确定A点的坐标.
因为A点在y轴上,所以x2-2=0,
所以x=± .
当x= 时,1-x=1- <0,
不符合A点在y轴的正半轴上,所以舍去.
当x=- 时,1-x=1+ >0,符合题意.
所以A点的坐标为(0,1+ ).已知点A(x2-2,1-x)在y轴的正半轴上,求A点的坐标.例3 解:知3-讲 点的特殊位置不仅要考虑点的横坐标,还要考虑
点的纵坐标,两者都要兼顾,缺一不可.1已知点A(a,-5),B(8,b),AB平行于x轴,且AB=3,求A,B两点的坐标.
若点P(m,1-2m)的横坐标与纵坐标互为相反
数,则点P一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
知3-练2知3-练3(2016·临夏州)已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限1. 平面直角坐标系的三要素:(1)两条数轴;(2)互相告
直;(3)公共原点.
2. 平面直角坐标系中两条数轴的特征:(1)互相垂直;
(2)原点重合;(3)通常取向上、向右为正方向;(4)
单 位长度一般取相同的.在有些实际问题中,两条
数轴上的单位长度可以不同.
3. 坐标轴上的点不属于任何象限;坐标平面内的任何
一个点,不在四个象限内就在坐标轴上.
标系1课堂讲解平面直角坐标系
各象限内、坐标轴上点的坐标特征特殊点的坐标的特征2课时流程逐点
导讲练课堂小结作业提升 笛卡尔(1596-1660) ,法国数学家、科学家和哲学
家. 早在1637年以前,他受到了经纬度的启发. (地理
上的经纬度是以赤道和本初子午线为标准的,这两条
线从局部上看可以看成平面内互相
垂直的两条线. )发明了平面直角坐
标系,又称笛卡尔坐标系.那么什么
是平面直角坐标系呢?我们今天就
来探讨一下,请随我进入今天的知
识博物馆参观参观!1知识点平面直角坐标系 下图是一条数轴,数轴上的点与实数是一一对应
的. 数轴上每个点都 对应一个实数,这个实数叫做这
个点在数轴上的坐标. 例如,点A在数轴上 的坐标为
-4,点B在数轴上的坐标为2. 反过来,知道数轴上一
个点的坐标, 这个点在数轴上的位置也就确定了. 例
如,数轴上坐标为5的点是点C.知1-导知1-导 类似于利用数轴确定直线上点的位置,能不能找
到一种办法来确定平面内的点的位置呢(例如图中A,
B,C,D各点)?知1-讲1. 坐标:数轴上的点可以用一个实数来表示,这个实
数叫做这个点在数轴上的坐标.
2. 平面直角坐标系:(1)定义:在平面内画两条互相垂
直、原点重合的数轴,组成平面直角坐标系.
(2)相关概念:水平的数轴称为x轴或横轴,习惯上取
向右为正方向;竖直的数轴称为y轴或纵轴,取向
上为正方向;两个坐标轴的交点为平面直角坐标系
的原点.知1-讲要点精析:
(1)一般情况下,平面直角坐标系的两条坐标轴的单位
长度是一致的;但在实际问题中,受两轴表示的实
际意义的影响,两坐标轴的单位长度可以有所不同.
(2) 4个半轴根据实际问题的需要,可画得长些或短些,
但原点必须画出.知1-讲下列语句不正确的是( )
A.平面直角坐标系中,两条互相垂直的数轴的交点是原点
B.平面直角坐标系所在的平面叫坐标平面
C.平面直角坐标系中x轴、y轴把坐标平面分成4部分
D.凡是两条互相垂直的直线都能组成平面直角坐标系例1 D知1-讲导引:本题主要考查平面直角坐标系的概念.根据平
面直角坐标系的概念可知A,B,C项正确.D
项不正确,因为平面直角坐标系必须由数轴构
成,且构成平面直角坐标系的两条数轴互相垂
直、原点重合.知1-讲 本题应用定义法,要正确理解平面直角坐标系的
概念.
理解并认识平面直角坐标系必须明确:(1)建立平
面直角坐标系的平面叫坐标平面;(2)平面直角坐标系
必须具备:①由两条数轴组成;②这两条数轴有公共
原点且互相垂直.知1-练1下列说法错误的是( )
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限知1-练2下列选项中,平面直角坐标系的画法正确的
是( )2知识点各象限内、坐标轴上点的坐标特征知2-导 有了平面直角坐标系,
平面内的点就可以用一个
有序数对来表示了. 例如,
如图,由点A分别向x轴和
y轴作垂线,垂足M在x轴
上的坐标是3,垂足N在y
轴上的坐标是 4,我们说知2-导点A的横坐标是3,纵坐标是4,有序数对(3, 4)就叫做
点A的坐标 (coordinate),记作A(3,4). 类似地,请你
写出点B,C,D的坐标: B(__,__), C(__ ,__),
D(__,__) .建立了平面直角坐标系以后,坐标平面就被两条坐标
轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分(如图),每个部分称
为象限(quadrant),分别
叫做第一象限、 第二象
限、第三象限和第四象
限.坐标轴上的点不属于
任何象限.知2-导知2-讲1. 象限的划分:如图,建立平面直角坐标系后,平
面被坐标轴分成四部分,分别叫第一象限、第二
象限、第三象限、第四象限,坐标轴上的点不属
于任何象限.知2-讲2.平面直角坐标系中各区域的点的坐标的特征:知2-讲例在平面直角坐标系(如图)中描出下列各点:
A(4,5),
B(-2,3),
C(-4,-1),
D(2.5,-2),
E(0,-4).例2 知2-讲解:如图,先在x轴上找出表示4的点,再在y轴上找出
表示5的点,过这两个点分别作x轴和y轴的垂线,
垂线的交点就是点A.
类似地,请你在图上
描出点B,C,D,E.知2-讲 由点的坐标确定点的位置的方法:方法一是由点
的坐标的符号确定点的位置,即(+,+)的点在第一
象限,(-,+)的点在第二象限,(-,-)的点在第三
象限,(+,-)的点在第四象限;方法二是分别过两
坐标轴上表示该点的坐标的点作两坐标轴的垂线,这
两条垂线的交点位置即为该点的位置.知2-练1写出图中点A,B,C,D,E,F的坐标.
知2-练2在图中描出下列各点:
L(-5,-3),M(4, 0),N(-6, 2),P(5,-3.5),
O(0,5),R(6,2).
(2016·广东)在平面直角坐标系中,点P(-2,-3)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限3知2-练4如图,小手盖住的点的坐标可能为( )
A.(5,2) B.(-6,3)
C.(-4,-6) D.(3,-4)3知识点特殊点的坐标的特征知3-导思考
原点O的坐标是什么? x轴和y轴上的点的坐标有什么
特点?
可以看出,原点O的坐标为(0,0);
x轴上的点的纵坐标为0,例如(1,0), (-1,0),…;
y轴上的点的横坐标为0,例如(0,1),(0,-1),… .
知3-导知3-讲导引:根据点在y轴上的特征:横坐标为0,可求出x的
值,然后再确定A点的坐标.
因为A点在y轴上,所以x2-2=0,
所以x=± .
当x= 时,1-x=1- <0,
不符合A点在y轴的正半轴上,所以舍去.
当x=- 时,1-x=1+ >0,符合题意.
所以A点的坐标为(0,1+ ).已知点A(x2-2,1-x)在y轴的正半轴上,求A点的坐标.例3 解:知3-讲 点的特殊位置不仅要考虑点的横坐标,还要考虑
点的纵坐标,两者都要兼顾,缺一不可.1已知点A(a,-5),B(8,b),AB平行于x轴,且AB=3,求A,B两点的坐标.
若点P(m,1-2m)的横坐标与纵坐标互为相反
数,则点P一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
知3-练2知3-练3(2016·临夏州)已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限1. 平面直角坐标系的三要素:(1)两条数轴;(2)互相告
直;(3)公共原点.
2. 平面直角坐标系中两条数轴的特征:(1)互相垂直;
(2)原点重合;(3)通常取向上、向右为正方向;(4)
单 位长度一般取相同的.在有些实际问题中,两条
数轴上的单位长度可以不同.
3. 坐标轴上的点不属于任何象限;坐标平面内的任何
一个点,不在四个象限内就在坐标轴上.
