8.2.2 加减消元法课件
图片预览











文档简介
课件34张PPT。第八章 二元一次方程组8.2 消元——解二元一次方程组第2课时 加减消元法1课堂讲解直接加减消元
先变形,再加减消元
用加减法解方程组2课时流程逐点
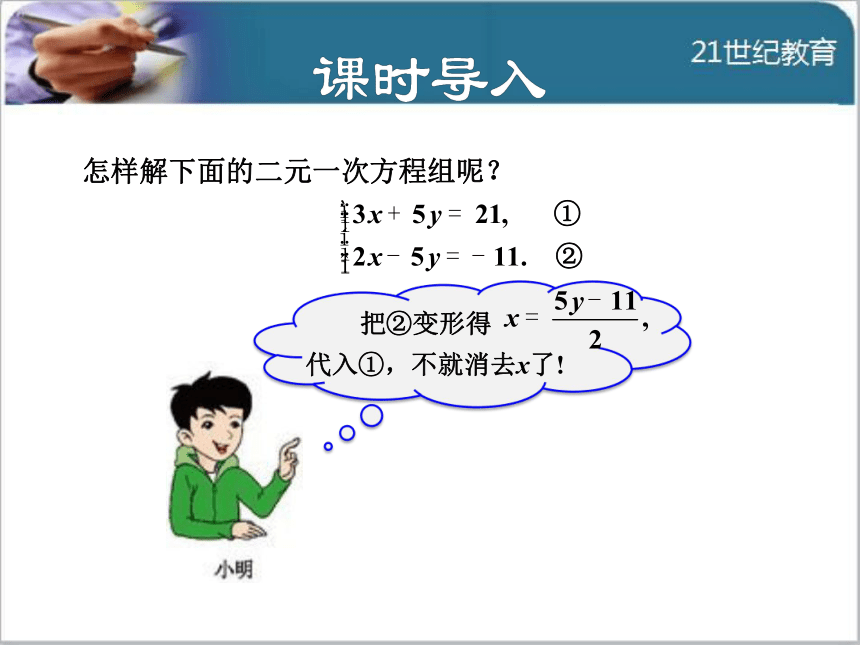
导讲练课堂小结作业提升 把②变形得 代入①,不就消去x了!怎样解下面的二元一次方程组呢?按小丽的思路,你能消去一个未知数吗? 把②变形得5y=2x
+11,可以直接代入①呀! 5y和-5y互为
相反数……两个方程相加,可以得到5x = 10,
x = 2.
将x = 2代入①,得 6 + 5y = 21,
y = 3.
所以方程组 的解是1知识点直接加减消元思考:
前面我们用代入法求出了方程组
的解. 这个方程组的两个方程中,y的系数有什么关
系?利用这种关系你能发现新的消元方法吗?知1-导知1-导 这两个方程中未知数y的系数相等,②-①
可消去未知数y,得 x=6.
把x=6代入①,得 y=4.
所以这个方程组的解是知1-导思考:
联系上面的解法,想一想怎样解方程组知1-导 从上面两个方程组的解法可以看出:当二元一
次方程组的两个方程中同一未知数的系数相反或相
等时,把这两个方程的两边分别相加或相减,就能
消去这个未知数,得到一个一元一次方程. 这种方
法叫做加减消元法,简称加减法
(addition-subtraction method).用加减法解方程组:
知1-讲例1导引:两个方程中x的系数相同,y的系数互为相反数,
这样可以把两个方程相加消去y,或者把两个方
程相减消去x.
方法一:①+②,得6x=12,解得x=2.把x=2
代入②,得3×2+7y=13,解得y=1.所以原方
程组的解为解:知1-讲方法二:①-②,得-14y=-14,解得y=1.
把y=1代入①,得3x-7×1=-1,解得x=2.
所以原方程组的解为 当二元一次方程组的两个方程中同一未知数
的系数相反或相等时,把这两个方程的两边分别相
加或相减,就能消去这个未知数,得到一个一元一
次方程,然后解答方程即可.知1-讲1 用加减法解方程组:知1-练2 方程组 中,x的系数的特点是_______,
方程组 中,y的系数的特点是_______,
这两个方程组用________消元法解较简便.知1-练3 用加减法解方程组 时,
①-②得( )
A.5y=2 B.-11y=8
C.-11y=2 D.5y=8
知1-练2知识点先变形,再加减消元知2-导 如果二元一次方程组的未知数的系数相同或
互为相反数,我们可以运用加减法来解.那么对
于一些系数不同或不互为相反数的二元一次方程
组,还能用加减法来解吗?用加减法解方程组:
知2-讲例2
这两个方程中没有同一个未知数的系数相反或相
等,直接加减这两 个方程不能消元. 我们对方程
变形,使得这两个方程中某个未知数的系数相反
或相等.分析:知2-讲解:①×3,得 9x+12y=48. ③
②×2,得 10x-12y=66. ④
③+④,得19x=114,
即 x=6.
把x=6代入① ,得 3×6+4y=16,
4y= -2,
y=
所以这个方程组的解是 例3 解方程组:
导引:方程组中,两个方程中y的系数的绝对值成倍数
关系,方程②乘以3就可与方程①相加消去y.
解: 由②×3,得 51x-9y=222,③
由①+③,得 59x=295,解得 x=5.
把x=5代入①,得8×5+9y=73,解得
所以原方程组的解为知2-讲1 用加减法解下列方程组:知2-练2 (2015·河北)利用加减消元法解方程组
下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
知2-练3 已知方程组 由②×3-①×2可
得到( )
A.-3y=2 B.4y+1=0
C.y=0 D.7y=-8知2-练知3-讲3知识点用加减法解方程组2台大收割机和5台小收割机同时工作2 h共收割小麦3. 6 hm2, 3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2. 1台大收割机和1台小收割机每小时各收割小麦多少公顷? 例4 知3-讲导引:如果1台大收割机和1台小收割机每小时各收割小
麦x hm2和y hm2, 那么2台大收割机和5台小收割
机同时工作1 h共收割小麦_____________ hm2,
3台大收割机和2台小收割机同时工作1 h共收割
小麦________hm2. 由此考虑两种情况下的工作
量.知3-讲解:设1台大收割机和1台小收割机每小时各收割小麦
x hm2和y hm2. 根据两种工作方式中的相等关系,
得方程组
去括号,得
②-①,得11x=4.4.
解这个方程,得x=0.4.知3-讲把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
答:1台大收割机和1台小收割机每小时各收割小
麦0. 4 hm2和0. 2 hm2 上面知3-讲 例5 解方程组:
导引:方程①和②中x,y的系数的绝对值都不相等,
也不成倍数关系,应取系数的绝对值的最小
公倍数6,可以先消去x,也可以先消去y.解:方法一:①×3,得6x+9y=9.③
②×2,得6x+4y=22.④
③-④,得5y=-13,即
把
解得
所以这个方程组的解为知3-讲代入①,得方法二:①×2,得4x+6y=6.⑤
②×3,得9x+6y=33.⑥
⑥-⑤,得5x=27,解得
把
解得
所以这个方程组的解为知3-讲代入①,得知3-讲 用加减消元法解二元一次方程组时,一般有三种
情况:
①方程组中某个未知数的系数的绝对值相等,则直接
利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,
但某个未知数的系数的绝对值成倍数关系,则其中
一个方程乘这个倍数后再利用加减法求解;知3-讲③方程组中任一个未知数的系数的绝对值既不相等,
也不成倍数关系,可利用最小公倍数的知识,把两
个方程都适当地乘一个数,使某个未知数的系数的
绝对值相等,然后再利用加减法求解.运输360 t化肥,装载了 6节火车车厢和15辆汽车;运输440 t化肥,装载了 8节火车车厢和10辆汽车. 每节火车车厢与每辆汽车平均各装多少吨化肥?知3-练解方程组.(2015·荆州)知3-练2用加减消元法解二元一次方程组的一般步骤: (1)变形:将方程组中某一未知数的系数变为相等或
相反.
(2)加减:消去一个未知数.
(3)求解:得到一个未知数的值.
(4)回代:求另一个未知数的值.
(5)写出解.
先变形,再加减消元
用加减法解方程组2课时流程逐点
导讲练课堂小结作业提升 把②变形得 代入①,不就消去x了!怎样解下面的二元一次方程组呢?按小丽的思路,你能消去一个未知数吗? 把②变形得5y=2x
+11,可以直接代入①呀! 5y和-5y互为
相反数……两个方程相加,可以得到5x = 10,
x = 2.
将x = 2代入①,得 6 + 5y = 21,
y = 3.
所以方程组 的解是1知识点直接加减消元思考:
前面我们用代入法求出了方程组
的解. 这个方程组的两个方程中,y的系数有什么关
系?利用这种关系你能发现新的消元方法吗?知1-导知1-导 这两个方程中未知数y的系数相等,②-①
可消去未知数y,得 x=6.
把x=6代入①,得 y=4.
所以这个方程组的解是知1-导思考:
联系上面的解法,想一想怎样解方程组知1-导 从上面两个方程组的解法可以看出:当二元一
次方程组的两个方程中同一未知数的系数相反或相
等时,把这两个方程的两边分别相加或相减,就能
消去这个未知数,得到一个一元一次方程. 这种方
法叫做加减消元法,简称加减法
(addition-subtraction method).用加减法解方程组:
知1-讲例1导引:两个方程中x的系数相同,y的系数互为相反数,
这样可以把两个方程相加消去y,或者把两个方
程相减消去x.
方法一:①+②,得6x=12,解得x=2.把x=2
代入②,得3×2+7y=13,解得y=1.所以原方
程组的解为解:知1-讲方法二:①-②,得-14y=-14,解得y=1.
把y=1代入①,得3x-7×1=-1,解得x=2.
所以原方程组的解为 当二元一次方程组的两个方程中同一未知数
的系数相反或相等时,把这两个方程的两边分别相
加或相减,就能消去这个未知数,得到一个一元一
次方程,然后解答方程即可.知1-讲1 用加减法解方程组:知1-练2 方程组 中,x的系数的特点是_______,
方程组 中,y的系数的特点是_______,
这两个方程组用________消元法解较简便.知1-练3 用加减法解方程组 时,
①-②得( )
A.5y=2 B.-11y=8
C.-11y=2 D.5y=8
知1-练2知识点先变形,再加减消元知2-导 如果二元一次方程组的未知数的系数相同或
互为相反数,我们可以运用加减法来解.那么对
于一些系数不同或不互为相反数的二元一次方程
组,还能用加减法来解吗?用加减法解方程组:
知2-讲例2
这两个方程中没有同一个未知数的系数相反或相
等,直接加减这两 个方程不能消元. 我们对方程
变形,使得这两个方程中某个未知数的系数相反
或相等.分析:知2-讲解:①×3,得 9x+12y=48. ③
②×2,得 10x-12y=66. ④
③+④,得19x=114,
即 x=6.
把x=6代入① ,得 3×6+4y=16,
4y= -2,
y=
所以这个方程组的解是 例3 解方程组:
导引:方程组中,两个方程中y的系数的绝对值成倍数
关系,方程②乘以3就可与方程①相加消去y.
解: 由②×3,得 51x-9y=222,③
由①+③,得 59x=295,解得 x=5.
把x=5代入①,得8×5+9y=73,解得
所以原方程组的解为知2-讲1 用加减法解下列方程组:知2-练2 (2015·河北)利用加减消元法解方程组
下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
知2-练3 已知方程组 由②×3-①×2可
得到( )
A.-3y=2 B.4y+1=0
C.y=0 D.7y=-8知2-练知3-讲3知识点用加减法解方程组2台大收割机和5台小收割机同时工作2 h共收割小麦3. 6 hm2, 3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2. 1台大收割机和1台小收割机每小时各收割小麦多少公顷? 例4 知3-讲导引:如果1台大收割机和1台小收割机每小时各收割小
麦x hm2和y hm2, 那么2台大收割机和5台小收割
机同时工作1 h共收割小麦_____________ hm2,
3台大收割机和2台小收割机同时工作1 h共收割
小麦________hm2. 由此考虑两种情况下的工作
量.知3-讲解:设1台大收割机和1台小收割机每小时各收割小麦
x hm2和y hm2. 根据两种工作方式中的相等关系,
得方程组
去括号,得
②-①,得11x=4.4.
解这个方程,得x=0.4.知3-讲把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
答:1台大收割机和1台小收割机每小时各收割小
麦0. 4 hm2和0. 2 hm2 上面知3-讲 例5 解方程组:
导引:方程①和②中x,y的系数的绝对值都不相等,
也不成倍数关系,应取系数的绝对值的最小
公倍数6,可以先消去x,也可以先消去y.解:方法一:①×3,得6x+9y=9.③
②×2,得6x+4y=22.④
③-④,得5y=-13,即
把
解得
所以这个方程组的解为知3-讲代入①,得方法二:①×2,得4x+6y=6.⑤
②×3,得9x+6y=33.⑥
⑥-⑤,得5x=27,解得
把
解得
所以这个方程组的解为知3-讲代入①,得知3-讲 用加减消元法解二元一次方程组时,一般有三种
情况:
①方程组中某个未知数的系数的绝对值相等,则直接
利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,
但某个未知数的系数的绝对值成倍数关系,则其中
一个方程乘这个倍数后再利用加减法求解;知3-讲③方程组中任一个未知数的系数的绝对值既不相等,
也不成倍数关系,可利用最小公倍数的知识,把两
个方程都适当地乘一个数,使某个未知数的系数的
绝对值相等,然后再利用加减法求解.运输360 t化肥,装载了 6节火车车厢和15辆汽车;运输440 t化肥,装载了 8节火车车厢和10辆汽车. 每节火车车厢与每辆汽车平均各装多少吨化肥?知3-练解方程组.(2015·荆州)知3-练2用加减消元法解二元一次方程组的一般步骤: (1)变形:将方程组中某一未知数的系数变为相等或
相反.
(2)加减:消去一个未知数.
(3)求解:得到一个未知数的值.
(4)回代:求另一个未知数的值.
(5)写出解.
