9.1.3 不等式的性质的应用课件
图片预览








文档简介
课件20张PPT。9.1 不等式第3课时 不等式的性质
的应用第九章 不等式与不等式组1课堂讲解“≤”、“≥”的意义
不等式性质的应用2课时流程逐点
导讲练课堂小结作业提升 你见过如图所示的天平吗,想知道左右两个托盘
里的物体质量有何关系?它又与我们学习的等石油和
关系呢?请我们一
起进入今天的学习
吧!1知识点“≤”、“≥”的意义 像a≥b或a≤b这样的式子,也经常用来表 示两个数量
的大小关系. 例如,为了表示2011 年9月1日北京的最低
气温是19 °C,最高气温是28 °C,我们可以用t表示这
天的气温,t是随 时间变化的,但是它有一定的变化范围,
即t ≥ 19 °C并且t≤28 °C. 符号“≥”读作“大于 或等
于”,也可说是“不小于”;符号“≤”读作 “小于或
等于”,也可说是“不大于”. a≥b或a≤b形式的式子,具
有与前面所说的不等式的性 质类似的性质.知1-导知1-讲要点精析:
(1)符号“≥”和“≤”也是不等号,它与“>”和
“<”的区别在于不等号的两边可能相等;
(2)用不等号“≥”和“≤”连接的不等式仍然具有
不等式的性质.知1-讲用数轴表示不等式的解集时要“两定”:
一定边界点,
二定方向;
注意:
若不等号是“≥”或“≤”,则边界点是实心圆
点;若不等号是“>”或“<”,则边界点是空心
圆圈.用不等式表示下列语句并写出解集,然后在数轴上表示解集.
(1)x与4的差不小于6;
(2)x的3倍与1的差小于或等于8.知1-讲例1 导引:先根据语句表达的意思列出不等式,然后利用
不等式的性质求出不等式的解集,最后在数轴
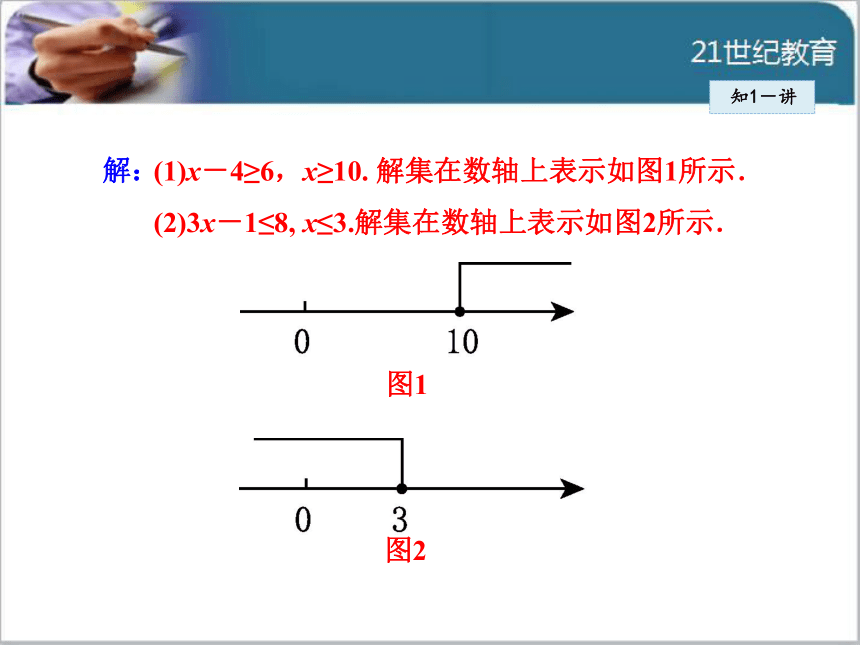
上表示出解集.知1-讲解:(1)x-4≥6,x≥10. 解集在数轴上表示如图1所示.
(2)3x-1≤8, x≤3.解集在数轴上表示如图2所示.知1-讲用数轴表示不等式解集的一般方法:
①画数轴;②定边界点,注意边界点是实心还是空心,
若边界点在解集内,则是实心圆点,若不在解集内,
则是空心圆圈;③定方向,原则是“小于向左,大于
向右”.用数轴表示不等式的解集,体现了一种重要
的数学思想——数形结合思想.1用不等式表示下列语句,并写出解集.
(1)x的5倍与1的差不大于9;
(2)x的相反数不小于-1.知1-练2满足不等式x-2≤3的自然数是( )
A.1、2、3、4、5
B.0、1、2、3、4、5
C.0、1、2、3、4
D.无数多个知1-练知1-练3(2015·泉州)把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )知1-练4不等式-2x+a≥2的解集如图所示,则a的值是( )
A.0
B.2
C.-2
D.42知识点不等式性质的应用知2-讲某长方体形状的容器长5 cm,宽3 cm, 高10 cm.容器内原有水的高度为3 cm,
现准备向它继续注水. 用V
(单位:cm3)表示新注入水
的体积,写出V的取值范围 .例2 知2-讲解:新注入水的体积V与原有水的体积的和不能超过
容器的容积,即 V+3×5×3≤3×5×10,
V≤105.
又由于新注入水的体积V不能是负数,因 此,V
的取值范围是 V≥0 并且 V≤105.
在数轴上表示V的取值范围如图所示.知2-讲 列不等式解决实际问题时,要抓住题目中的
关键词,利用关键词的意思列出准确的不等式 .1一次知识竞赛中,一共有25道题,答对一道题得10分,答错(或不答)一道题扣5分.设小明同学在这次竞赛中答对了x道题.
(1)根据所给条件,完成下表:
(2)若小明同学的竞赛成绩超过100分,则他至少答对多少道题?知2-练2若7x+2<7y+2,则x______y(填“>”“<”或“=”).它经历了________步,第一步是将不等式7x+2<7y+2的两边____________,第二步是将不等式的两边____________.
(2015·黄石)当1≤x≤2时,ax+2>0,则a的取值范围是( )
A.a>-1 B.a>-2
C.a>0 D.a>-1且a≠0知2-练3某种品牌的八宝粥,外包装标明:净含量为330±10 g,表明了这罐八宝粥的净含量x的
范围是( )
A.320 g<x<340 g
B.320 g≤x<340 g
C.320 g<x≤340 g
D.320 g≤x≤340 g知2-练41. 利用不等式的性质2,3可以把未知数的系数化为1,
但要注意乘(或除以)同一个负数时,不等号要改变
方向.
2. 利用不等式的性质解决实际问题时,要辨别“至
多”“至少”“不足”“超过”等反映不等关系的
关键词的含义.明确:若x≥a,则x有最小值a;若
x≤b,则x有最大值b;若x>a或x<b,则x既无最大
值也无最小值.
的应用第九章 不等式与不等式组1课堂讲解“≤”、“≥”的意义
不等式性质的应用2课时流程逐点
导讲练课堂小结作业提升 你见过如图所示的天平吗,想知道左右两个托盘
里的物体质量有何关系?它又与我们学习的等石油和
关系呢?请我们一
起进入今天的学习
吧!1知识点“≤”、“≥”的意义 像a≥b或a≤b这样的式子,也经常用来表 示两个数量
的大小关系. 例如,为了表示2011 年9月1日北京的最低
气温是19 °C,最高气温是28 °C,我们可以用t表示这
天的气温,t是随 时间变化的,但是它有一定的变化范围,
即t ≥ 19 °C并且t≤28 °C. 符号“≥”读作“大于 或等
于”,也可说是“不小于”;符号“≤”读作 “小于或
等于”,也可说是“不大于”. a≥b或a≤b形式的式子,具
有与前面所说的不等式的性 质类似的性质.知1-导知1-讲要点精析:
(1)符号“≥”和“≤”也是不等号,它与“>”和
“<”的区别在于不等号的两边可能相等;
(2)用不等号“≥”和“≤”连接的不等式仍然具有
不等式的性质.知1-讲用数轴表示不等式的解集时要“两定”:
一定边界点,
二定方向;
注意:
若不等号是“≥”或“≤”,则边界点是实心圆
点;若不等号是“>”或“<”,则边界点是空心
圆圈.用不等式表示下列语句并写出解集,然后在数轴上表示解集.
(1)x与4的差不小于6;
(2)x的3倍与1的差小于或等于8.知1-讲例1 导引:先根据语句表达的意思列出不等式,然后利用
不等式的性质求出不等式的解集,最后在数轴
上表示出解集.知1-讲解:(1)x-4≥6,x≥10. 解集在数轴上表示如图1所示.
(2)3x-1≤8, x≤3.解集在数轴上表示如图2所示.知1-讲用数轴表示不等式解集的一般方法:
①画数轴;②定边界点,注意边界点是实心还是空心,
若边界点在解集内,则是实心圆点,若不在解集内,
则是空心圆圈;③定方向,原则是“小于向左,大于
向右”.用数轴表示不等式的解集,体现了一种重要
的数学思想——数形结合思想.1用不等式表示下列语句,并写出解集.
(1)x的5倍与1的差不大于9;
(2)x的相反数不小于-1.知1-练2满足不等式x-2≤3的自然数是( )
A.1、2、3、4、5
B.0、1、2、3、4、5
C.0、1、2、3、4
D.无数多个知1-练知1-练3(2015·泉州)把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )知1-练4不等式-2x+a≥2的解集如图所示,则a的值是( )
A.0
B.2
C.-2
D.42知识点不等式性质的应用知2-讲某长方体形状的容器长5 cm,宽3 cm, 高10 cm.容器内原有水的高度为3 cm,
现准备向它继续注水. 用V
(单位:cm3)表示新注入水
的体积,写出V的取值范围 .例2 知2-讲解:新注入水的体积V与原有水的体积的和不能超过
容器的容积,即 V+3×5×3≤3×5×10,
V≤105.
又由于新注入水的体积V不能是负数,因 此,V
的取值范围是 V≥0 并且 V≤105.
在数轴上表示V的取值范围如图所示.知2-讲 列不等式解决实际问题时,要抓住题目中的
关键词,利用关键词的意思列出准确的不等式 .1一次知识竞赛中,一共有25道题,答对一道题得10分,答错(或不答)一道题扣5分.设小明同学在这次竞赛中答对了x道题.
(1)根据所给条件,完成下表:
(2)若小明同学的竞赛成绩超过100分,则他至少答对多少道题?知2-练2若7x+2<7y+2,则x______y(填“>”“<”或“=”).它经历了________步,第一步是将不等式7x+2<7y+2的两边____________,第二步是将不等式的两边____________.
(2015·黄石)当1≤x≤2时,ax+2>0,则a的取值范围是( )
A.a>-1 B.a>-2
C.a>0 D.a>-1且a≠0知2-练3某种品牌的八宝粥,外包装标明:净含量为330±10 g,表明了这罐八宝粥的净含量x的
范围是( )
A.320 g<x<340 g
B.320 g≤x<340 g
C.320 g<x≤340 g
D.320 g≤x≤340 g知2-练41. 利用不等式的性质2,3可以把未知数的系数化为1,
但要注意乘(或除以)同一个负数时,不等号要改变
方向.
2. 利用不等式的性质解决实际问题时,要辨别“至
多”“至少”“不足”“超过”等反映不等关系的
关键词的含义.明确:若x≥a,则x有最小值a;若
x≤b,则x有最大值b;若x>a或x<b,则x既无最大
值也无最小值.
