16.1.2 二次根式的性质课件
图片预览








文档简介
课件24张PPT。第十六章 二次根式16.1 二次根式第2课时 二次根式的
性质1课堂讲解2课时流程逐点
导讲练课堂小结作业提升性质1:( )2=a(a≥0)
性质2: =a(a≥0)
代数式 在很很久以前,欧几里得做了一个奇怪的梦,在梦里上帝要他求出 和( )2的结果,欧几里得想啊,做啊,就是完不成这个任务,所以他也就一直没有睡醒,你能帮帮欧几里得,让他快点醒来吗?1知识点性质1:( )2=a(a≥0)探究根据算术平方根的意义填空:( )2=________;
( )2=________; =________;( )2=__________.
是4的算术平方根,根据算术平方根的意义, 是一
个平方等于4的非负数.因此有( )2=4.同理, 分别是
2, ,0的算术平方根.因此有( )2=2, = ,( )2=0.知1-导归 纳知1-导一般地:( )2=a(a≥0). 即 (a≥0).是一个非负数,表示非负数a的算术平方
根,因此通过算术平方根的定义,将非负数a的算术平方
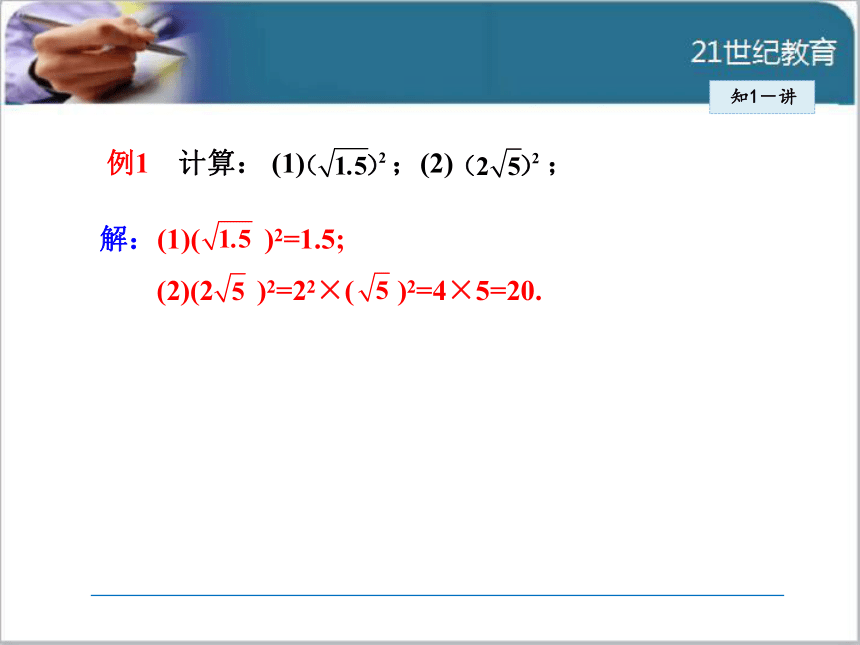
根平方,就等于它本身,即 ( )2=a(a≥0).知1-讲解:(1)( )2=1.5;
(2)(2 )2=22×( )2=4×5=20.例1 计算: (1) ;(2) ;知1-讲总 结知1-讲 ( )2=a(a≥0)这一性质也可以反过来用,即a =
( )2(a≥0),如3=( )2, 等.1 计算:(1)( )2; (2)( 3 )2.知1-练2 下列计算正确的是( )
A.-( )2=-6 B.( )2=9
C.( )2=±16 D.
3 把4 写成一个正数的平方的形式是( )
A. B. C. D.知1-练2知识点知2-导填空: =________; =________;
=________; =________;
可以得到 =2, =0.1, = , =0.性质2: =a(a≥0)探究归 纳知2-导一般地,根据算术平方根的意义, =a(a≥0). 当a是负数时,如 , 说明此
时的结果是a的相反数-a.
故此公式可以写为 ,如果没有
特别说明,被开方式中的所有字母均表示正数.
点拨:
运用公式 进行化简时,一定要
先确定 a的取值范围.知2-讲知2-讲例2 化简: (1) ; (2) .解: (1)
(2)总 结知2-讲 计算 一般有两个步骤:①去掉根号及被开方数
的指数,写成绝对值的形式,即 =|a|;②去掉绝对
值符号,根据绝对值的意义进行化简,即|a|=1 说出下列各式的值:
(1) (2)
(3) (4)知2-练知2-练2 下列式子成立的是( )
A. =-13 B.- =-0.6
C. =13 D. =±6
3 如果 =1-2a,则( )
A.a< B.a≤ C.a> D.a≥知3-导3知识点代数式 回顾我们学过的式子,如5,a,a+b,-ab, ,
-x3, , (a≥0),它们都是用基本运算符号(基本
运算包括加、减、乘、除、乘方和开方)把数或表示
数的字母连接起来的式子,我们称这样的式子为代数
式(algebraic expression).1.定义:用基本运算符号(基本运算包括加、减、乘、除、乘方
和开方)把数或表示数的字母连接起来的式子称为代数式,例
如:3,x,x+y, (x≥0),ab, (t≠0),x3都是代数式.
要点精析:(1)代数式是数或字母之间的运算关系,代数式中只能
含运算符号,不能含“>”“≥”“<”“≤”“≠”或“=”等关系符号.
(2)代数式的书写规则:①除数与数相乘以外,代数式中的“×”
简写为“·”或省略不写;②数与字母相乘时,数要写在字母的前
面,如果数是带分数,要化为假分数;③代数式中遇到除法运
算时,一般按分数的形式表示.
(3)单独的一个数或一个字母也是代数式.
2.易错警示:含有等号或不等号的式子不是代数式,如a>b,
a=b不是代数式.知3-讲例3 指出下列式子,哪些是代数式,哪些不是代数式?
(1)a=b;(2)a-b;(3)2x-1=3;(4)1;(5)2+3- ;
(6)3-4x>6;(7)(a+b)(a-b);(8) 知3-讲分析:代数式是运用运算符号把数或表示数的字母连起来
的式子.(1)(3)是等式,所以不是代数式;(6)是不等
式,所以不是代数式;(2)(5)(7)(8)是运用运算符号
连接起来的式子,所以代数式;(4)是单独的一个数,
也是代数式.
解:(2)(4)(5)(7)(8)是代数式;(1)(3)(6)不是代数式.总 结知3-讲 解题时先看是不是有运算符号连接,再找单独的
字母或数字.只要不是运算符号连接的式子就不是代数
式.事实上,只要式子中含有“<”、“>”、“≤”、
“≥”、“=”、“≠”的式子都不是代数式.1 在式子-3x,6-y=3,4xy2, ,π,a, ,
3a+2b中,是代数式的有( )个
A.4 B.5 C.6 D.7
2 (规律探究题)观察如图所示的图形,则第n个图形中
三角形的个数是________.知3-练(1) 具有双重非负性:①a≥0;② ≥0.
(2) 与( )2的区别与联系:
区别:①取值范围不同: 中a为全体实数,( )2中
a≥0;②运算顺序不同: 是先平方后开方,( )2是
先开方后平方;
③运算结果不同: =|a|= ( )2=a.
联系: 与( )2均为非负数,且当a≥0时, =
( )2.
(3)计算(b )2时,运用(ab)2=a2b2这个结论可知,
(b )2=b2a. 我们学过的式子,如4,a,a+b,ab, ,x3, (a
≥0) , ,它们都是用基本运算符号把数或表示数的字母
连起来的式子,我们称这样的式子为代数式.
注意:1.基本运算符号是指基本运算包括加、减、乘、
除、乘方和开方.
2.单独一个数字或一个字母也是代数式.我们学过的整
式、分式都是代数式.
3. 只要式子中含有“<”、“>”、“≤”、“≥”、
“=”、“≠”的式子都不是代数式.
性质1课堂讲解2课时流程逐点
导讲练课堂小结作业提升性质1:( )2=a(a≥0)
性质2: =a(a≥0)
代数式 在很很久以前,欧几里得做了一个奇怪的梦,在梦里上帝要他求出 和( )2的结果,欧几里得想啊,做啊,就是完不成这个任务,所以他也就一直没有睡醒,你能帮帮欧几里得,让他快点醒来吗?1知识点性质1:( )2=a(a≥0)探究根据算术平方根的意义填空:( )2=________;
( )2=________; =________;( )2=__________.
是4的算术平方根,根据算术平方根的意义, 是一
个平方等于4的非负数.因此有( )2=4.同理, 分别是
2, ,0的算术平方根.因此有( )2=2, = ,( )2=0.知1-导归 纳知1-导一般地:( )2=a(a≥0). 即 (a≥0).是一个非负数,表示非负数a的算术平方
根,因此通过算术平方根的定义,将非负数a的算术平方
根平方,就等于它本身,即 ( )2=a(a≥0).知1-讲解:(1)( )2=1.5;
(2)(2 )2=22×( )2=4×5=20.例1 计算: (1) ;(2) ;知1-讲总 结知1-讲 ( )2=a(a≥0)这一性质也可以反过来用,即a =
( )2(a≥0),如3=( )2, 等.1 计算:(1)( )2; (2)( 3 )2.知1-练2 下列计算正确的是( )
A.-( )2=-6 B.( )2=9
C.( )2=±16 D.
3 把4 写成一个正数的平方的形式是( )
A. B. C. D.知1-练2知识点知2-导填空: =________; =________;
=________; =________;
可以得到 =2, =0.1, = , =0.性质2: =a(a≥0)探究归 纳知2-导一般地,根据算术平方根的意义, =a(a≥0). 当a是负数时,如 , 说明此
时的结果是a的相反数-a.
故此公式可以写为 ,如果没有
特别说明,被开方式中的所有字母均表示正数.
点拨:
运用公式 进行化简时,一定要
先确定 a的取值范围.知2-讲知2-讲例2 化简: (1) ; (2) .解: (1)
(2)总 结知2-讲 计算 一般有两个步骤:①去掉根号及被开方数
的指数,写成绝对值的形式,即 =|a|;②去掉绝对
值符号,根据绝对值的意义进行化简,即|a|=1 说出下列各式的值:
(1) (2)
(3) (4)知2-练知2-练2 下列式子成立的是( )
A. =-13 B.- =-0.6
C. =13 D. =±6
3 如果 =1-2a,则( )
A.a< B.a≤ C.a> D.a≥知3-导3知识点代数式 回顾我们学过的式子,如5,a,a+b,-ab, ,
-x3, , (a≥0),它们都是用基本运算符号(基本
运算包括加、减、乘、除、乘方和开方)把数或表示
数的字母连接起来的式子,我们称这样的式子为代数
式(algebraic expression).1.定义:用基本运算符号(基本运算包括加、减、乘、除、乘方
和开方)把数或表示数的字母连接起来的式子称为代数式,例
如:3,x,x+y, (x≥0),ab, (t≠0),x3都是代数式.
要点精析:(1)代数式是数或字母之间的运算关系,代数式中只能
含运算符号,不能含“>”“≥”“<”“≤”“≠”或“=”等关系符号.
(2)代数式的书写规则:①除数与数相乘以外,代数式中的“×”
简写为“·”或省略不写;②数与字母相乘时,数要写在字母的前
面,如果数是带分数,要化为假分数;③代数式中遇到除法运
算时,一般按分数的形式表示.
(3)单独的一个数或一个字母也是代数式.
2.易错警示:含有等号或不等号的式子不是代数式,如a>b,
a=b不是代数式.知3-讲例3 指出下列式子,哪些是代数式,哪些不是代数式?
(1)a=b;(2)a-b;(3)2x-1=3;(4)1;(5)2+3- ;
(6)3-4x>6;(7)(a+b)(a-b);(8) 知3-讲分析:代数式是运用运算符号把数或表示数的字母连起来
的式子.(1)(3)是等式,所以不是代数式;(6)是不等
式,所以不是代数式;(2)(5)(7)(8)是运用运算符号
连接起来的式子,所以代数式;(4)是单独的一个数,
也是代数式.
解:(2)(4)(5)(7)(8)是代数式;(1)(3)(6)不是代数式.总 结知3-讲 解题时先看是不是有运算符号连接,再找单独的
字母或数字.只要不是运算符号连接的式子就不是代数
式.事实上,只要式子中含有“<”、“>”、“≤”、
“≥”、“=”、“≠”的式子都不是代数式.1 在式子-3x,6-y=3,4xy2, ,π,a, ,
3a+2b中,是代数式的有( )个
A.4 B.5 C.6 D.7
2 (规律探究题)观察如图所示的图形,则第n个图形中
三角形的个数是________.知3-练(1) 具有双重非负性:①a≥0;② ≥0.
(2) 与( )2的区别与联系:
区别:①取值范围不同: 中a为全体实数,( )2中
a≥0;②运算顺序不同: 是先平方后开方,( )2是
先开方后平方;
③运算结果不同: =|a|= ( )2=a.
联系: 与( )2均为非负数,且当a≥0时, =
( )2.
(3)计算(b )2时,运用(ab)2=a2b2这个结论可知,
(b )2=b2a. 我们学过的式子,如4,a,a+b,ab, ,x3, (a
≥0) , ,它们都是用基本运算符号把数或表示数的字母
连起来的式子,我们称这样的式子为代数式.
注意:1.基本运算符号是指基本运算包括加、减、乘、
除、乘方和开方.
2.单独一个数字或一个字母也是代数式.我们学过的整
式、分式都是代数式.
3. 只要式子中含有“<”、“>”、“≤”、“≥”、
“=”、“≠”的式子都不是代数式.
