17.1.1 勾股定理课件
图片预览











文档简介
(共30张PPT)
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
勾股定理
勾股定理与面积的关系
如图是2002年在北京召开的国际数学家大会(ICM—
2002)的会标.它的设计思路可追溯到3世纪中国数学家赵爽
所使用的弦图.用弦图证明勾股定理在数学史上有着重要
的地位.
1
知识点
勾股定理
问题1
图中三个正方形的面积有什么关系?等腰直角三角形
的三边之间有什么关系?
知1-导
归 纳
知1-导
可以发现,以等腰直角三角形两直角边为边长的
小正方形的面积的和,等于以斜边为边长的大正方形
的面积. 即等腰直角三角形的三边之间有一种特殊的
关系:斜边的平方等于两直角边的平方和.
等腰直角三角形有上述性质,
其他的直角三角形也有这个性质
吗?图中,每个小方格的面积均
为1,请分别算出图中正方形 A,
B,C,A', B', C'的面积,看
看能得出什么结论.(提示:以斜边为边长的正方形的面积,
等于某个正方形的面积减去4个直角三 角形的面积.)
知1-导
问题2
归 纳
知1-导
命题1 如果直角三角形的两条直角边长分别为a,
b,斜边长为c,那么a2+b2=c2.
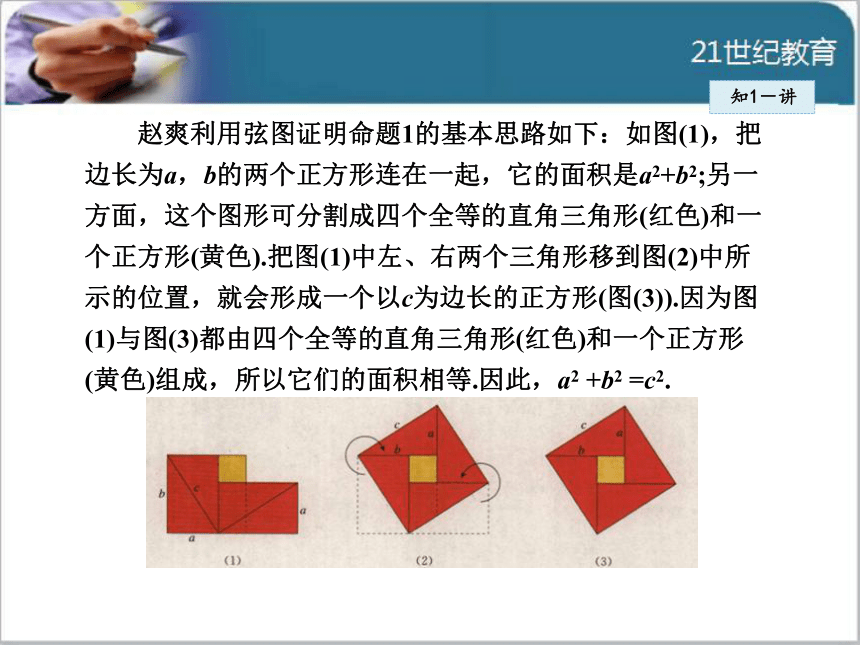
赵爽利用弦图证明命题1的基本思路如下:如图(1),把
边长为a,b的两个正方形连在一起,它的面积是a2+b2;另一
方面,这个图形可分割成四个全等的直角三角形(红色)和一
个正方形(黄色).把图(1)中左、右两个三角形移到图(2)中所
示的位置,就会形成一个以c为边长的正方形(图(3)).因为图
(1)与图(3)都由四个全等的直角三角形(红色)和一个正方形
(黄色)组成,所以它们的面积相等.因此,a2 +b2 =c2.
知1-讲
总 结
知1-讲
勾股定理:直角三角形的两条直角边的平方和等于斜边的
平方;
数学表达式:在Rt△ABC中,∠C=90°,AB=c,AC=b,
BC=a,则a2+b2=c2.
要点精析:(1)勾股定理适用于任何一个直角三角形;
(2)勾股定理的内容描述的是直角三角形三边之间的数量关
系,已知其中任意两边可以求出第三边;
(3)勾股定理的变形公式:a2=c2-b2,b2=c2-a2;
(4)运用勾股定理时,要分清斜边、直角边.
分清斜边和直角边.因为在Rt△ABC中,a,b,
c是三边,所以可以用勾股定理解决问题.
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的
对边分别是a,b,c.
(1)已知a=b=6,求c;
(2)已知c=3,b=2,求a;
(3)已知a∶b=2∶1,c=5,求b.
知1-讲
导引:
(1)∵∠C=90°,a=b=6,
∴由勾股定理,得
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=
知1-讲
解:
总 结
知1-讲
利用勾股定理求直角三角形的边长的方法:一般
都要经过“一分二代三化简”这“三步曲”,即一分:分
清哪条边是斜边,哪些是直角边;二代:将已知边长
及两边之间的关系式代入a2+b2=c2(假设c是斜边);
三化简.
1 设直角三角形的两条直角边长分别为a和b,斜边
长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
知1-练
2 (2016·株洲)如图,以直角三角形的三边a,b,c为
边或直径,分别向外作等边三角形,半圆,等腰直
角三角形和正方形,上述四种情况的面积关系满足
S1+S2=S3的图形个数是( )
A.1 B.2 C.3 D.4
知1-练
3 若一个直角三角形的两直角边的长分别为a,b,
斜边长为c,则下列关于a,b,c的关系式中不正
确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
知1-练
错解:第三边的长为
错解分析:由于习惯了“勾三股四弦五”的说法,故将题意理
解为两直角边长分别为3和4,于是斜边长为5.但这一理解
的前提是3,4为直角边长,而题中并未加以任何说明,因
而所求的第三边可能为斜边,也可能为直角边.所以需要
分情况求解.
正确解法:(1)当两直角边长分别为3和4时,
第三边的长为
(2)当斜边长为4,一直角边长为3时,
第三边的长为
例2 已知直角三角形的两边长分别为3,4,求第三边的长.
知1-讲
总 结
知1-讲
运用勾股定理求第三边的长时,一般要经过“一分
二代三化简”这三步曲;若由题目中的条件找不到斜边,
则需要运用分类讨论思想求解.
1 (1)已知一直角三角形的两边长分别为8,15,
则第三边长为____________;
(2)已知一直角三角形的两边长分别为2和4,则第
三边长的平方为__________.
知1-练
2 (2015·黔西南)一直角三角形的两边长分别为
3和4,则第三边长为( )
A.5 B. C. D.5或
知1-练
2
知识点
勾股定理与面积的关系
知2-导
在一张纸上画4个与图所示的全等的直角三边形,
并把它们剪下来.如图所示,用这四个直角三角形进
行拼摆,将得到一个以a+b为边长的大正方形和以直
角形斜边c为边长的小正方形.
归 纳
知2-导
观察图形,容易得到大正方形的边长为 a+b,所以
大正方形的面积是(a+b)2.又因为大正方形是由4个全等
的直角三角形和中间的正方形拼成的,所以大正方形的
面积又可表示成 ab×4+c2. 因此有(a+b)2= ab×4+
c2.整理得a2+b2=c2,即a、b、c为边的直角三角形满足
两直角边的平方和等于斜边的平方.
知2-讲
例3 观察如图所示的图形,回答问题:
(1)如图①,△DEF为直角三角形,正方形 P的面积
为9,正方形Q的面积为
15,则正方形M的面积
为________;
(2)如图②,分别以直角
三角形ABC的三边长为直径向三角形外作三个半圆,
则这三个半圆形的面积之间的关系式是________;
(用图中字母表示)
(3)如图③,如果直角三角形两直角边的长分别为3和
4,分别以直角三角形的三边长为直径作半圆,请你
利用(2)中得出的结论求阴影部分的面积.
知2-讲
(1)根据正方形的面积公式,结合勾股定理可得
DF2=DE2+EF2,即正方形M的面积=9+15=24;
(2)
另外由勾股定理可知AC2+BC2=AB2,所以S1+S2=S3;
(3)阴影部分的面积=两个小半圆形的面积和+直角三角
形的面积-大半圆形的面积,由(2)可知两个小半圆形
的面积和=大半圆形的面积,所以阴影部分的面积=
直角三角形的面积.
导引:
知2-讲
(1)24
(2)S1+S2=S3
(3)设两个小半圆形的面积分别为S1,S2,大半圆
形的面积为S3,三角形的面积为S△,
则S阴影=S1+S2+S△-S3
=S△= ×3×4=6.
解:
总 结
知2-讲
与直角三角形三边相连的正方形、半圆及正多边形、
圆都具有相同的结论:两直角边上图形面积的和等于斜
边上的图形面积.本例考查了勾股定理及正方形的面积
公式,半圆形面积的求法,解答此类题目的关键是仔细
观察所给图形,面积与边长、直径有平方关系,就很容
易联想到勾股定理.
1 如图,图中所有的三角形都是直角三角形,四边
形都是正方形.已知正方形A,B,C,D的边长分
别是12,16,9,12,求最大正方形E的面积.
知2-练
知2-练
2 如图,字母B所代表的正方形的面积是( )
A.12
B.13
C.144
D.194
知2-练
3 如图,直线l上有三个正方形a,b,c,若a,c的面
积分别为3和4,则b的面积为( )
A.3
B.4
C.5
D.7
1.运用勾股定理时应注意以下几点:
(1)遇到求线段长度的问题时,能想到用勾股定理.
(2)必须把要求的线段归结到直角三角形中去(没有直角
三角形,可以通过作辅助线构造直角三角形),切忌
乱用勾股定理.
(3)分清组成直角三角形的线段中哪条是直角边,哪条
是斜边.
2.勾股定理适用的前提条件是直角三角形:
由公式a2+b2=c2可知,在直角三角形中,已知任
意两条边长,可求第三条边长.在应用公式计算时
要会灵活变形,常常要与乘法公式结合使用;
如c2=a2+b2=(a+b)2-2ab或
c2=a2+b2=(a-b)2 + 2ab;
a2=c2-b2=(c+b)(c-b)等.
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
1
课堂讲解
2
课时流程
逐点
导讲练
课堂小结
作业提升
勾股定理
勾股定理与面积的关系
如图是2002年在北京召开的国际数学家大会(ICM—
2002)的会标.它的设计思路可追溯到3世纪中国数学家赵爽
所使用的弦图.用弦图证明勾股定理在数学史上有着重要
的地位.
1
知识点
勾股定理
问题1
图中三个正方形的面积有什么关系?等腰直角三角形
的三边之间有什么关系?
知1-导
归 纳
知1-导
可以发现,以等腰直角三角形两直角边为边长的
小正方形的面积的和,等于以斜边为边长的大正方形
的面积. 即等腰直角三角形的三边之间有一种特殊的
关系:斜边的平方等于两直角边的平方和.
等腰直角三角形有上述性质,
其他的直角三角形也有这个性质
吗?图中,每个小方格的面积均
为1,请分别算出图中正方形 A,
B,C,A', B', C'的面积,看
看能得出什么结论.(提示:以斜边为边长的正方形的面积,
等于某个正方形的面积减去4个直角三 角形的面积.)
知1-导
问题2
归 纳
知1-导
命题1 如果直角三角形的两条直角边长分别为a,
b,斜边长为c,那么a2+b2=c2.
赵爽利用弦图证明命题1的基本思路如下:如图(1),把
边长为a,b的两个正方形连在一起,它的面积是a2+b2;另一
方面,这个图形可分割成四个全等的直角三角形(红色)和一
个正方形(黄色).把图(1)中左、右两个三角形移到图(2)中所
示的位置,就会形成一个以c为边长的正方形(图(3)).因为图
(1)与图(3)都由四个全等的直角三角形(红色)和一个正方形
(黄色)组成,所以它们的面积相等.因此,a2 +b2 =c2.
知1-讲
总 结
知1-讲
勾股定理:直角三角形的两条直角边的平方和等于斜边的
平方;
数学表达式:在Rt△ABC中,∠C=90°,AB=c,AC=b,
BC=a,则a2+b2=c2.
要点精析:(1)勾股定理适用于任何一个直角三角形;
(2)勾股定理的内容描述的是直角三角形三边之间的数量关
系,已知其中任意两边可以求出第三边;
(3)勾股定理的变形公式:a2=c2-b2,b2=c2-a2;
(4)运用勾股定理时,要分清斜边、直角边.
分清斜边和直角边.因为在Rt△ABC中,a,b,
c是三边,所以可以用勾股定理解决问题.
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的
对边分别是a,b,c.
(1)已知a=b=6,求c;
(2)已知c=3,b=2,求a;
(3)已知a∶b=2∶1,c=5,求b.
知1-讲
导引:
(1)∵∠C=90°,a=b=6,
∴由勾股定理,得
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=
知1-讲
解:
总 结
知1-讲
利用勾股定理求直角三角形的边长的方法:一般
都要经过“一分二代三化简”这“三步曲”,即一分:分
清哪条边是斜边,哪些是直角边;二代:将已知边长
及两边之间的关系式代入a2+b2=c2(假设c是斜边);
三化简.
1 设直角三角形的两条直角边长分别为a和b,斜边
长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
知1-练
2 (2016·株洲)如图,以直角三角形的三边a,b,c为
边或直径,分别向外作等边三角形,半圆,等腰直
角三角形和正方形,上述四种情况的面积关系满足
S1+S2=S3的图形个数是( )
A.1 B.2 C.3 D.4
知1-练
3 若一个直角三角形的两直角边的长分别为a,b,
斜边长为c,则下列关于a,b,c的关系式中不正
确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
知1-练
错解:第三边的长为
错解分析:由于习惯了“勾三股四弦五”的说法,故将题意理
解为两直角边长分别为3和4,于是斜边长为5.但这一理解
的前提是3,4为直角边长,而题中并未加以任何说明,因
而所求的第三边可能为斜边,也可能为直角边.所以需要
分情况求解.
正确解法:(1)当两直角边长分别为3和4时,
第三边的长为
(2)当斜边长为4,一直角边长为3时,
第三边的长为
例2 已知直角三角形的两边长分别为3,4,求第三边的长.
知1-讲
总 结
知1-讲
运用勾股定理求第三边的长时,一般要经过“一分
二代三化简”这三步曲;若由题目中的条件找不到斜边,
则需要运用分类讨论思想求解.
1 (1)已知一直角三角形的两边长分别为8,15,
则第三边长为____________;
(2)已知一直角三角形的两边长分别为2和4,则第
三边长的平方为__________.
知1-练
2 (2015·黔西南)一直角三角形的两边长分别为
3和4,则第三边长为( )
A.5 B. C. D.5或
知1-练
2
知识点
勾股定理与面积的关系
知2-导
在一张纸上画4个与图所示的全等的直角三边形,
并把它们剪下来.如图所示,用这四个直角三角形进
行拼摆,将得到一个以a+b为边长的大正方形和以直
角形斜边c为边长的小正方形.
归 纳
知2-导
观察图形,容易得到大正方形的边长为 a+b,所以
大正方形的面积是(a+b)2.又因为大正方形是由4个全等
的直角三角形和中间的正方形拼成的,所以大正方形的
面积又可表示成 ab×4+c2. 因此有(a+b)2= ab×4+
c2.整理得a2+b2=c2,即a、b、c为边的直角三角形满足
两直角边的平方和等于斜边的平方.
知2-讲
例3 观察如图所示的图形,回答问题:
(1)如图①,△DEF为直角三角形,正方形 P的面积
为9,正方形Q的面积为
15,则正方形M的面积
为________;
(2)如图②,分别以直角
三角形ABC的三边长为直径向三角形外作三个半圆,
则这三个半圆形的面积之间的关系式是________;
(用图中字母表示)
(3)如图③,如果直角三角形两直角边的长分别为3和
4,分别以直角三角形的三边长为直径作半圆,请你
利用(2)中得出的结论求阴影部分的面积.
知2-讲
(1)根据正方形的面积公式,结合勾股定理可得
DF2=DE2+EF2,即正方形M的面积=9+15=24;
(2)
另外由勾股定理可知AC2+BC2=AB2,所以S1+S2=S3;
(3)阴影部分的面积=两个小半圆形的面积和+直角三角
形的面积-大半圆形的面积,由(2)可知两个小半圆形
的面积和=大半圆形的面积,所以阴影部分的面积=
直角三角形的面积.
导引:
知2-讲
(1)24
(2)S1+S2=S3
(3)设两个小半圆形的面积分别为S1,S2,大半圆
形的面积为S3,三角形的面积为S△,
则S阴影=S1+S2+S△-S3
=S△= ×3×4=6.
解:
总 结
知2-讲
与直角三角形三边相连的正方形、半圆及正多边形、
圆都具有相同的结论:两直角边上图形面积的和等于斜
边上的图形面积.本例考查了勾股定理及正方形的面积
公式,半圆形面积的求法,解答此类题目的关键是仔细
观察所给图形,面积与边长、直径有平方关系,就很容
易联想到勾股定理.
1 如图,图中所有的三角形都是直角三角形,四边
形都是正方形.已知正方形A,B,C,D的边长分
别是12,16,9,12,求最大正方形E的面积.
知2-练
知2-练
2 如图,字母B所代表的正方形的面积是( )
A.12
B.13
C.144
D.194
知2-练
3 如图,直线l上有三个正方形a,b,c,若a,c的面
积分别为3和4,则b的面积为( )
A.3
B.4
C.5
D.7
1.运用勾股定理时应注意以下几点:
(1)遇到求线段长度的问题时,能想到用勾股定理.
(2)必须把要求的线段归结到直角三角形中去(没有直角
三角形,可以通过作辅助线构造直角三角形),切忌
乱用勾股定理.
(3)分清组成直角三角形的线段中哪条是直角边,哪条
是斜边.
2.勾股定理适用的前提条件是直角三角形:
由公式a2+b2=c2可知,在直角三角形中,已知任
意两条边长,可求第三条边长.在应用公式计算时
要会灵活变形,常常要与乘法公式结合使用;
如c2=a2+b2=(a+b)2-2ab或
c2=a2+b2=(a-b)2 + 2ab;
a2=c2-b2=(c+b)(c-b)等.
