18.1.1 平行四边形的边、角性质 课件
文档属性
| 名称 | 18.1.1 平行四边形的边、角性质 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 550.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 15:52:53 | ||
图片预览










文档简介
课件35张PPT。第十八章 平行四边形18.1 平行四边形第1课时 平行四边形的
边、角性质1课堂讲解平行四边形的定义
平行四边形的性质——对边相等
平行四边形的性质——对角相等
平行线之间的距离2课时流程逐点
导讲练课堂小结作业提升 平行四边形是常见的图形.小区的伸缩门、庭院的
竹篱笆、载重汽车的防护栏等,都有平行四边形的形
象.你还能举出一些例子吗?1知识点平行四边形的定义 我们知道,两组对边分别平行的四
边形叫做平行四边形(parallelogram ).平
行四边形用“? ”表示,如图,平行四
边形ABCD记作“?ABCD”.知1-导1.定义:两组对边分别平行的四边形叫做平行四
边形.
2.表示方法:平行四边形用符号“?”表示;
如图.平行四边形ABCD记作“?ABCD”,
读作“平行四边形ABCD”.
3.数学表达式: ?四边形ABCD是平行
四边形.即:若AB∥CD,AD∥BC,则四边形
ABCD是平行四边形;若四边形ABCD是平行四
边形,则AB∥CD,AD∥BC.知1-讲要点精析:
(1)平行四边形的定义有两个要素:
①是四边形;②两组对边分别平行.
作为四边形,平行四边形具有一般四边形的一切性
质.如有四条边,四个内角,两条对角线,内角和
为360°,外角和为360°等.
作为平行四边形,它区别于其他一般四边形的特殊
性质为:平行四边形的两组对边分别平行;知1-讲 (2)平行四边形的定义既是它的一个性质,又是它的
一种判定方法;∵四边形ABCD是平行四边形,
∴ 反过来,∵ ∴四边形
ABCD是平行四边形.
4.易错警示:平行四边形的表示要按一定方向依次表
示各个顶点;它既可以按顺时针方向排列字母顺序,
也可以按逆时针方向排列字母顺序,但不能打乱顺
序.知1-讲例1 如图,在?ABCD中,过点P作直线EF,GH分别平
行于AB,BC,那么图中共有______
个平行四边形.知1-讲导引:根据平行四边形的定义,知AB∥CD,AD∥BC,由
已知可知,EF∥AB,GH∥BC,所以根据平行四边
形的定义可以判定四边形ABFE是平行四边形,同理
可判定四边形EFCD、四边形AGHD、四边形GBCH、
四边形AGPE、四边形EPHD、四边形GBFP、四边
形PFCH都是平行四边形,最后还要加上?ABCD,
即共有9个平行四边形.9知1-讲 平行四边形的定义的功能:平行四边形的定义既是
平行四边形的性质:平行四边形的两组对边分别平行;
又是判定平行四边形的一种方法:两组对边分别平行的
四边形是平行四边形.即对于任何一个几何定义,都具
有两种功能,顺用是它的判定,逆用是它的性质.
对于几何计数问题,要按照一定的顺序(如从小到大
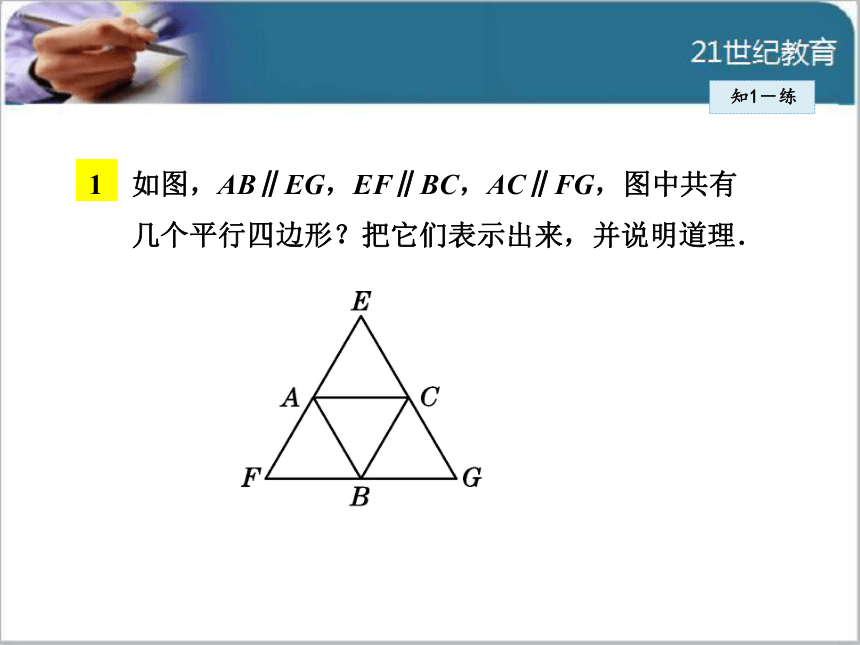
等)分类计数,做到不重复不遗漏.1 如图,AB∥EG,EF∥BC,AC∥FG,图中共有
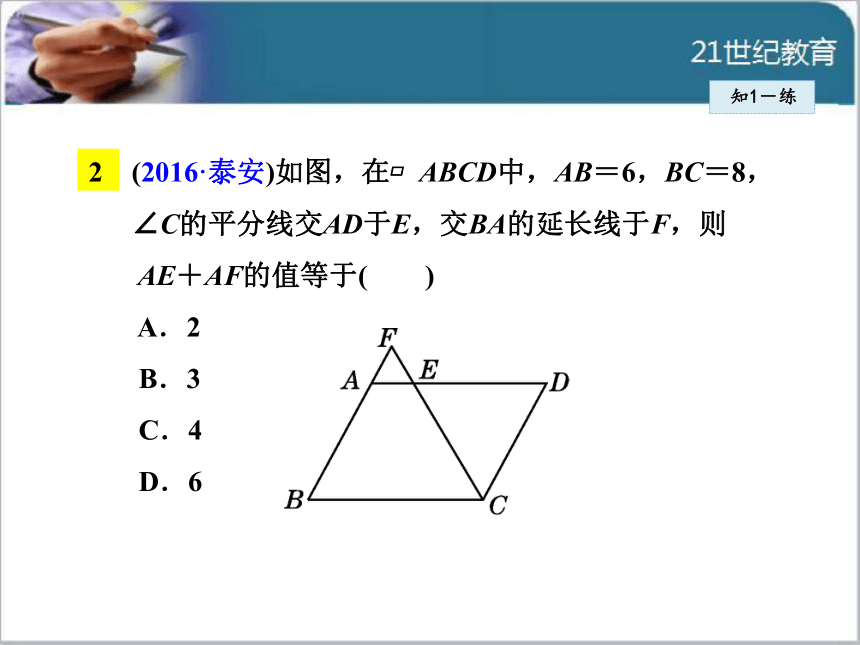
几个平行四边形?把它们表示出来,并说明道理.知1-练(2016·泰安)如图,在?ABCD中,AB=6,BC=8,
∠C的平分线交AD于E,交BA的延长线于F,则
AE+AF的值等于( )
A.2
B.3
C.4
D.6知1-练2知识点平行四边形的性质——对边相等知2-导 根据定义画一个平行四边形,观察它,除了“两组
对边分别平行”外,它的边之间还有什么关系?
通过观察和度量,我们猜想:平行四边形的对边相
等;下面我们对它进行证明.
上述猜想涉及线段相等. 我们知道, 利用三角形全
等得出全等三角形的对应边是证明线段相等的一种重要
的方法.为此,我们通过添加辅助线,构造两个 三角形,
通过三角形全等进行证明.探究知2-导如图,连接AC.
∵AD//BC,AB//CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA.
∴AD=CD,AB=CD.证明:知2-导这样我们证明了平行四边形具有以下性质:
平行四边形的对边相等.知2-讲边的性质:平行四边形对边平行;平行四边形对边
相等.
数学表达式:如图,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
AB=CD,AD=BC.知2-讲例2 如图 ,在? ABCD 中,DE⊥AB,BF⊥CD,
垂足分别为E,F.求证AE=CF.∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又 ∠AED=∠CFB = 90。,
∴△ADE≌△CBF.
∴ AE=CF.证明:知2-讲 在四边形中证明四边形的对边相等,经常证明四
边形是平行四边形,利用平行四边形的性质定理——
对边相等来得到线段相等.1 在? ABCD 中,已知AB=5,BC=3,求它的周长.
2 如图,剪两张对边平行的纸条,随意交叉叠放在一
起, 重合的部分构成了一个四边形.转动其中一张纸
条,线段 AD和BC的长度有什么关系?为什么?知2-练知2-练3 (2015·广州)已知?ABCD的周长为32,AB=4,则
BC等于( )
A.4 B.12 C.24 D.28
4 (2015·玉林、防城港)如图,在?ABCD中,BM是
∠ABC的平分线,交CD于点M,且MC=2,
?ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.43知识点平行四边形的性质——对角相等知3-导 根据定义画一个平行四边形,观察它,除了“两组
对边分别平行”外,它的角之间还有什么关系?度量一
下,和你的猜想一致吗?
通过观察和度量,我们猜想:平行四边形的对角相
等;下面我们对它进行证明.
上述猜想涉及角相等.我们知道, 利用三角形全等
得出全等三角形的对应角都相等,是证角相等的一种重
要 的方法.为此,我们通过添加辅助线,构造两个三角
形,通过三角形全等进行证明.探究知3-导如图,连接AC.
∵AD//BC,AB//CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA.
∴∠B=∠D.
请同学们自己证明∠BAD=∠DCB.证明:知3-导这样我们证明了平行四边形具有以下性质:
平行四边形的对角相等.知3-讲角的性质:平行四边形对角相等;平行四边形邻角互补.
数学表达式:如图,
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∠A+∠B=180°,∠B+∠C=180°,
∠C+∠D=180°,∠A+∠D=180°.知3-讲例3 如图,在?ABCD中,已知∠A+∠C=120°,求平
行四边形各角的度数.
由平行四边形的对角相等,
得∠A=∠C,结合已知条件
∠A+∠C=120°,即可求出∠A和∠C的度数;
再根据平行线的性质,进而求出∠B,∠D的度数.
在?ABCD中,∠A=∠C,∠B=∠D.
∵∠A+∠C=120°,∴∠A=∠C=60°.
∵∠D=180°-∠A=180°-60°=120°.
∴∠B=∠D=120°.解: 导引:知3-讲 平行四边形中求有关角度的基本方法是利用平
行四边形对角相等,邻角互补的性质,并且已知一
个角或已知两邻角的关系可求出其他三个角的度数.在? ABCD 中,已知∠A = 38°,求其余各内
角的度数.知3-练2 (2016·衢州)如图,在?ABCD中,M是BC延长线上的
一点,若∠A=135°,则∠MCD的度数是( )
A.45° B.55°
C.65° D.75°
3 如图,在?ABCD中,CE⊥AB,E为垂足,如果∠A
=120°,那么∠BCE的度数是( )
A.80° B.50°
C.40° D.30°知3-练知4-导4知识点平行线之间的距离 距离是几何中的重要度量之一 .前面我们已经学习了点
与点之间的距离、点到直线的距离.在此基础上,我们结合
平行四边形的概念和性质,介绍两条平行线之间的距离.
如图,a//b, c//d,c,d与a,b分别相
交于A,B,C,D四点. 由平行四边形的概
念和性质可知,四边形ABDC是平行四边
形,AB=CD.也就是说,两条平行线之间的任何两条平行
线段都相等.知4-导 从上面的结论可以知道,如果两条直线平行,那么
一条直线上所有的点到另一条直线的距离都相等.两条平
行线中,一条直线上任意一点到另一条直线的距离,叫
做这两条平行线之间的距离. 如图,
a∥b, A是a上的任意一点,
AB⊥b, B是垂足,线段AB
的长就是a,b之间的距离.定义:两条平行线中,一条直线上任意一点到另一条
直线的距离,叫做这两条平行线之间的距离.
要点精析:(1)点到直线的距离是指这点到这条直线的
垂线段的长度;
(2)三种距离之间的区别与联系知4-讲例4 如图所示,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,
G为垂足,则下列结论中错误的
是( )
A.AB=CD
B.CE=FG
C.A,B两点间的距离就是线段AB的长
D.直线a,b间的距离就是线段CD的长
根据“两点间的距离”,“两平行线间的距离”的有
关概念和定理,可以作出判断.知4-讲D导引:知4-讲 如果两条直线平行,那么一条直线上的所有点到另
一条直线的距离相等;即:平行线间的距离处处相等.
(1)“平行线间的距离处处相等”,在作平行四边形的高
时,可根据需要灵活选择位置;(注:平行线的这一
性质常用来解决三角形同底等高问题)
(2)平行线的位置确定后,它们间的距离是定值(是正值),
不随垂线段位置的改变而改变.1 如图,a∥b,AB⊥直线a于点A,CD⊥直线b于
点C,则:
(1)点B与点D的距离是指线段________的长;
(2)点D到直线b的距离是指线段________的长;
(3)两平行线a,b间的距离是线段________或
________的长.知4-练2 如图,在?ABCD中,对角线AC=21 cm,BE⊥AC
于E,且BE=5 cm,AD=7 cm,则AD和BC之间的
距离为________.知4-练1.平行四边形的定义既可当性质用,又可当判定用.
2.平行四边形的边角的性质为证明线段的平行和相等、
角的互补和相等提供了很重要的依据.注意常和全
等三角形一起综合运用.
3.平行线间的距离是指垂线段的长度,平行线的位置
确定了,它们之间的距离就是定值,不随着垂线段
的位置的改变而改变.
边、角性质1课堂讲解平行四边形的定义
平行四边形的性质——对边相等
平行四边形的性质——对角相等
平行线之间的距离2课时流程逐点
导讲练课堂小结作业提升 平行四边形是常见的图形.小区的伸缩门、庭院的
竹篱笆、载重汽车的防护栏等,都有平行四边形的形
象.你还能举出一些例子吗?1知识点平行四边形的定义 我们知道,两组对边分别平行的四
边形叫做平行四边形(parallelogram ).平
行四边形用“? ”表示,如图,平行四
边形ABCD记作“?ABCD”.知1-导1.定义:两组对边分别平行的四边形叫做平行四
边形.
2.表示方法:平行四边形用符号“?”表示;
如图.平行四边形ABCD记作“?ABCD”,
读作“平行四边形ABCD”.
3.数学表达式: ?四边形ABCD是平行
四边形.即:若AB∥CD,AD∥BC,则四边形
ABCD是平行四边形;若四边形ABCD是平行四
边形,则AB∥CD,AD∥BC.知1-讲要点精析:
(1)平行四边形的定义有两个要素:
①是四边形;②两组对边分别平行.
作为四边形,平行四边形具有一般四边形的一切性
质.如有四条边,四个内角,两条对角线,内角和
为360°,外角和为360°等.
作为平行四边形,它区别于其他一般四边形的特殊
性质为:平行四边形的两组对边分别平行;知1-讲 (2)平行四边形的定义既是它的一个性质,又是它的
一种判定方法;∵四边形ABCD是平行四边形,
∴ 反过来,∵ ∴四边形
ABCD是平行四边形.
4.易错警示:平行四边形的表示要按一定方向依次表
示各个顶点;它既可以按顺时针方向排列字母顺序,
也可以按逆时针方向排列字母顺序,但不能打乱顺
序.知1-讲例1 如图,在?ABCD中,过点P作直线EF,GH分别平
行于AB,BC,那么图中共有______
个平行四边形.知1-讲导引:根据平行四边形的定义,知AB∥CD,AD∥BC,由
已知可知,EF∥AB,GH∥BC,所以根据平行四边
形的定义可以判定四边形ABFE是平行四边形,同理
可判定四边形EFCD、四边形AGHD、四边形GBCH、
四边形AGPE、四边形EPHD、四边形GBFP、四边
形PFCH都是平行四边形,最后还要加上?ABCD,
即共有9个平行四边形.9知1-讲 平行四边形的定义的功能:平行四边形的定义既是
平行四边形的性质:平行四边形的两组对边分别平行;
又是判定平行四边形的一种方法:两组对边分别平行的
四边形是平行四边形.即对于任何一个几何定义,都具
有两种功能,顺用是它的判定,逆用是它的性质.
对于几何计数问题,要按照一定的顺序(如从小到大
等)分类计数,做到不重复不遗漏.1 如图,AB∥EG,EF∥BC,AC∥FG,图中共有
几个平行四边形?把它们表示出来,并说明道理.知1-练(2016·泰安)如图,在?ABCD中,AB=6,BC=8,
∠C的平分线交AD于E,交BA的延长线于F,则
AE+AF的值等于( )
A.2
B.3
C.4
D.6知1-练2知识点平行四边形的性质——对边相等知2-导 根据定义画一个平行四边形,观察它,除了“两组
对边分别平行”外,它的边之间还有什么关系?
通过观察和度量,我们猜想:平行四边形的对边相
等;下面我们对它进行证明.
上述猜想涉及线段相等. 我们知道, 利用三角形全
等得出全等三角形的对应边是证明线段相等的一种重要
的方法.为此,我们通过添加辅助线,构造两个 三角形,
通过三角形全等进行证明.探究知2-导如图,连接AC.
∵AD//BC,AB//CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA.
∴AD=CD,AB=CD.证明:知2-导这样我们证明了平行四边形具有以下性质:
平行四边形的对边相等.知2-讲边的性质:平行四边形对边平行;平行四边形对边
相等.
数学表达式:如图,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
AB=CD,AD=BC.知2-讲例2 如图 ,在? ABCD 中,DE⊥AB,BF⊥CD,
垂足分别为E,F.求证AE=CF.∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又 ∠AED=∠CFB = 90。,
∴△ADE≌△CBF.
∴ AE=CF.证明:知2-讲 在四边形中证明四边形的对边相等,经常证明四
边形是平行四边形,利用平行四边形的性质定理——
对边相等来得到线段相等.1 在? ABCD 中,已知AB=5,BC=3,求它的周长.
2 如图,剪两张对边平行的纸条,随意交叉叠放在一
起, 重合的部分构成了一个四边形.转动其中一张纸
条,线段 AD和BC的长度有什么关系?为什么?知2-练知2-练3 (2015·广州)已知?ABCD的周长为32,AB=4,则
BC等于( )
A.4 B.12 C.24 D.28
4 (2015·玉林、防城港)如图,在?ABCD中,BM是
∠ABC的平分线,交CD于点M,且MC=2,
?ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.43知识点平行四边形的性质——对角相等知3-导 根据定义画一个平行四边形,观察它,除了“两组
对边分别平行”外,它的角之间还有什么关系?度量一
下,和你的猜想一致吗?
通过观察和度量,我们猜想:平行四边形的对角相
等;下面我们对它进行证明.
上述猜想涉及角相等.我们知道, 利用三角形全等
得出全等三角形的对应角都相等,是证角相等的一种重
要 的方法.为此,我们通过添加辅助线,构造两个三角
形,通过三角形全等进行证明.探究知3-导如图,连接AC.
∵AD//BC,AB//CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA.
∴∠B=∠D.
请同学们自己证明∠BAD=∠DCB.证明:知3-导这样我们证明了平行四边形具有以下性质:
平行四边形的对角相等.知3-讲角的性质:平行四边形对角相等;平行四边形邻角互补.
数学表达式:如图,
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∠A+∠B=180°,∠B+∠C=180°,
∠C+∠D=180°,∠A+∠D=180°.知3-讲例3 如图,在?ABCD中,已知∠A+∠C=120°,求平
行四边形各角的度数.
由平行四边形的对角相等,
得∠A=∠C,结合已知条件
∠A+∠C=120°,即可求出∠A和∠C的度数;
再根据平行线的性质,进而求出∠B,∠D的度数.
在?ABCD中,∠A=∠C,∠B=∠D.
∵∠A+∠C=120°,∴∠A=∠C=60°.
∵∠D=180°-∠A=180°-60°=120°.
∴∠B=∠D=120°.解: 导引:知3-讲 平行四边形中求有关角度的基本方法是利用平
行四边形对角相等,邻角互补的性质,并且已知一
个角或已知两邻角的关系可求出其他三个角的度数.在? ABCD 中,已知∠A = 38°,求其余各内
角的度数.知3-练2 (2016·衢州)如图,在?ABCD中,M是BC延长线上的
一点,若∠A=135°,则∠MCD的度数是( )
A.45° B.55°
C.65° D.75°
3 如图,在?ABCD中,CE⊥AB,E为垂足,如果∠A
=120°,那么∠BCE的度数是( )
A.80° B.50°
C.40° D.30°知3-练知4-导4知识点平行线之间的距离 距离是几何中的重要度量之一 .前面我们已经学习了点
与点之间的距离、点到直线的距离.在此基础上,我们结合
平行四边形的概念和性质,介绍两条平行线之间的距离.
如图,a//b, c//d,c,d与a,b分别相
交于A,B,C,D四点. 由平行四边形的概
念和性质可知,四边形ABDC是平行四边
形,AB=CD.也就是说,两条平行线之间的任何两条平行
线段都相等.知4-导 从上面的结论可以知道,如果两条直线平行,那么
一条直线上所有的点到另一条直线的距离都相等.两条平
行线中,一条直线上任意一点到另一条直线的距离,叫
做这两条平行线之间的距离. 如图,
a∥b, A是a上的任意一点,
AB⊥b, B是垂足,线段AB
的长就是a,b之间的距离.定义:两条平行线中,一条直线上任意一点到另一条
直线的距离,叫做这两条平行线之间的距离.
要点精析:(1)点到直线的距离是指这点到这条直线的
垂线段的长度;
(2)三种距离之间的区别与联系知4-讲例4 如图所示,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,
G为垂足,则下列结论中错误的
是( )
A.AB=CD
B.CE=FG
C.A,B两点间的距离就是线段AB的长
D.直线a,b间的距离就是线段CD的长
根据“两点间的距离”,“两平行线间的距离”的有
关概念和定理,可以作出判断.知4-讲D导引:知4-讲 如果两条直线平行,那么一条直线上的所有点到另
一条直线的距离相等;即:平行线间的距离处处相等.
(1)“平行线间的距离处处相等”,在作平行四边形的高
时,可根据需要灵活选择位置;(注:平行线的这一
性质常用来解决三角形同底等高问题)
(2)平行线的位置确定后,它们间的距离是定值(是正值),
不随垂线段位置的改变而改变.1 如图,a∥b,AB⊥直线a于点A,CD⊥直线b于
点C,则:
(1)点B与点D的距离是指线段________的长;
(2)点D到直线b的距离是指线段________的长;
(3)两平行线a,b间的距离是线段________或
________的长.知4-练2 如图,在?ABCD中,对角线AC=21 cm,BE⊥AC
于E,且BE=5 cm,AD=7 cm,则AD和BC之间的
距离为________.知4-练1.平行四边形的定义既可当性质用,又可当判定用.
2.平行四边形的边角的性质为证明线段的平行和相等、
角的互补和相等提供了很重要的依据.注意常和全
等三角形一起综合运用.
3.平行线间的距离是指垂线段的长度,平行线的位置
确定了,它们之间的距离就是定值,不随着垂线段
的位置的改变而改变.
