18.2.3 菱形及其性质课件
图片预览










文档简介
课件36张PPT。第十八章 平行四边形18.2 特殊的平行四边形第3课时 菱形及其性质1课堂讲解菱形的定义
菱形的边的性质
菱形的对角线的性质
菱形的对称性2课时流程逐点
导讲练课堂小结作业提升 菱形具有平行四边形的不稳定性,具有变化中
的不变性,有对称美在生活中,被人们广泛地采用,
如图为“中国花边”,其中就有很多菱形的图案.在
我们的周边,还有哪些物体是菱形的形状,用到菱
形的哪些性质?1知识点菱形的定义 我们观察平行四边形的一组邻边,如右图,当
这组邻边相等时,这时的平行四边形也是一个特殊
的平行四边形.有一组邻边相等的平行四边形叫做菱形(rhombus).
菱形也是常见的图形.一些门窗的窗格、美丽的中国结、伸缩
的衣帽架 (下图)等都有菱形的形象.你还能举出一些例子吗? 知1-导知1-讲定义:有一组邻边相等的平行四边形叫做菱形.
要点精析:
(1)菱形必须满足两个条件:一是平行四边形;二是
一组邻边相等.二者必须同时具备,缺一不可.
(2)菱形的定义既是菱形的基本性质,也是菱形的基
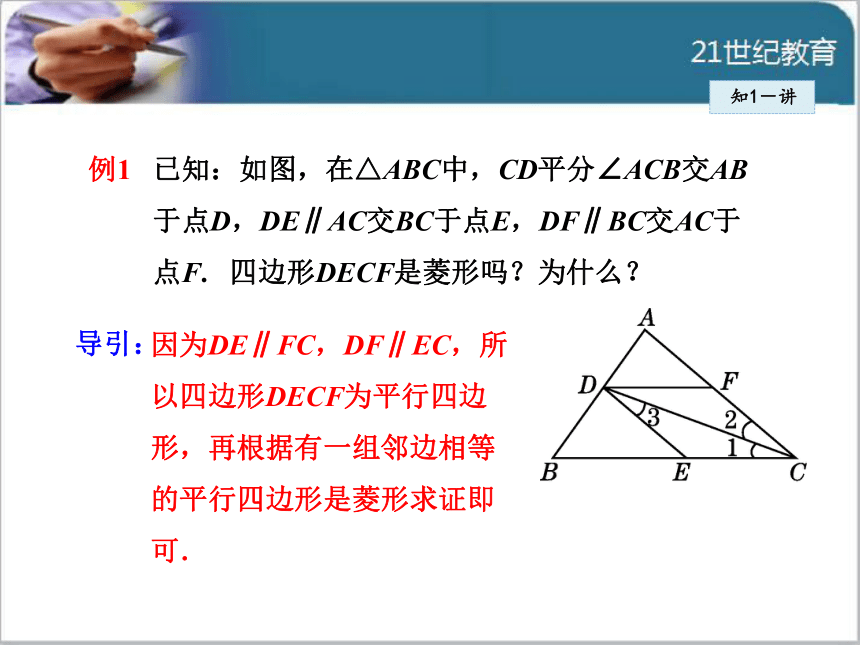
本判定方法.例1 已知:如图,在△ABC中,CD平分∠ACB交AB
于点D,DE∥AC交BC于点E,DF∥BC交AC于
点F. 四边形DECF是菱形吗?为什么?知1-讲因为DE∥FC,DF∥EC,所
以四边形DECF为平行四边
形,再根据有一组邻边相等
的平行四边形是菱形求证即
可.导引:知1-讲四边形DECF是菱形.理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD平分∠ACB,
∴∠1=∠2,∴∠1=∠3,∴DE=EC,
∴平行四边形DECF为菱形(有一组邻边相等的平
行四边形是菱形).解:知1-讲 本题考查了菱形的定义,菱形的定义也可
以作为菱形的判定方法.1 〈安顺〉如图,已知点D在△ABC的BC边上,DE
∥AC交AB于E,DF∥AB交AC于F.
(1)证明:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,
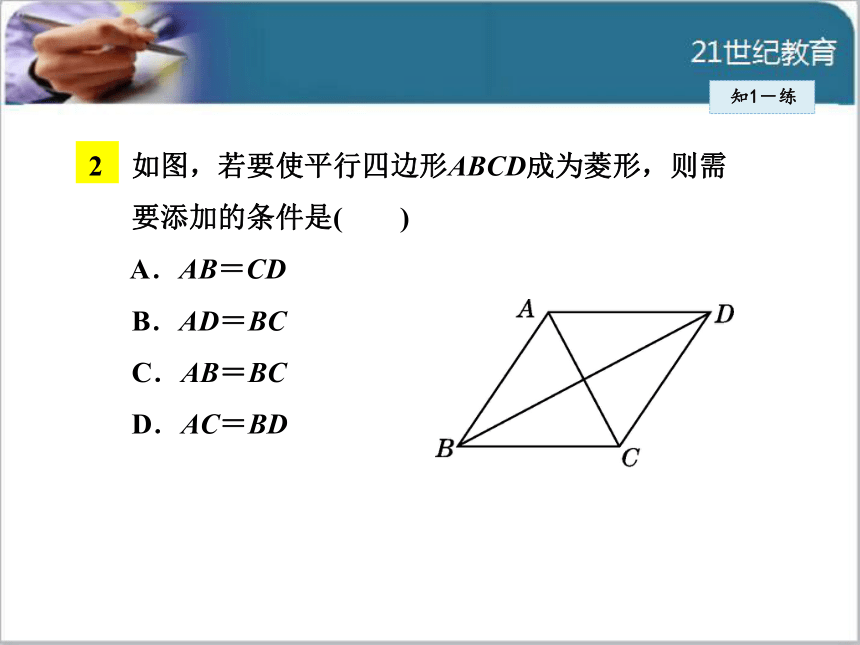
并说明理由.知1-练2 如图,若要使平行四边形ABCD成为菱形,则需
要添加的条件是( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD知1-练2知识点菱形的边的性质知2-导 菱形具有平行四边形的所有性质.此外,菱形
还具有哪些特殊性质呢? 根据菱形的轴对称性,你
发现菱形的四条边具有什么大小关系?问 题菱形的四条边都相等.知2-讲例2 如图所示,菱形ABCD中,∠B=60°,AB=2,
E、F分别是BC、CD的中点,连接AE、EF、
AF,则△AEF的周长为( )
A. B.
C. D.3 在菱形ABCD中,因为∠B=60°,连接AC,则
△ABC是等边三角形,又因为E分别是BC的中点,
所以AE垂直于BC,因此AE= ,所以
△AEF的周长为 ,故选B.B分析:知2-讲 在菱形中作辅助线经常连接对角线,构造
三角形来做题,能够迎刃而解.1 边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm C.12 cm D.15 cm
2 (2015·台州)如图,在菱形ABCD中,AB=8,点E,
F分别在AB,AD上,且AE=AF,过点E作EG∥AD
交CD于点G,过点F作FH∥AB交BC于点H,EG与
FH交于点O,当四边形AEOF与四边形CGOH的周长
之差为12时,AE的长为( )
A.6.5 B.6
C.5.5 D.5知2-练知2-练3 如图所示,在菱形ABCD中,AB = 5,∠BCD =?
120°,则对角线AC等于( )
A.20
B.15
C.10
D.53知识点菱形的对角线的性质知3-导 因为菱形是平行四边形,所以它具有平行四边形的
所有性质.由于它的一组邻边相等,它是否具有一般平行
四边形不具有的一些特殊性质呢?思考菱形的两条对角线AC与BD之间具有什么位置关系?知3-导 对于菱形,我们仍然从它的对角线等方面进行研
究.可以发现并证明(请你自己完成证明),菱形还有以
下性质:
菱形的两条对角线互相垂直,并且每一条对角线
平分一组对角.知3-导问 题菱形的面积如何计算呢?菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积
时,要灵活运用使计算简单.由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直平分,因此可以在直角
三角形中利用勾股定理来进行计算.知3-讲例3 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=12 cm,AC=6 cm.求菱形的周长.导引:∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,由勾股定理,
得AB=
∴菱形的周长=4AB知3-讲解:知3-讲 菱形的对角线将菱形分成四个全等的直角三角
形,我们通常将菱形问题中求相关线段的长转化为
求直角三角形中相关线段的长,再利用勾股定理来
计算.1 如图,四边形ABCD是菱形,BE⊥AD,BF⊥CD,
垂足分别为E,F.
(1)求证:BE=BF;
(2)当菱形ABCD的对角线AC=8,BD=6时,
求BE的长.知3-练2 (2016·枣庄)如图,四边形ABCD是菱形,AC=8,
DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4知3-练知3-讲如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小
路AC和BD. 求两条小路的长(结果保留小数点后
两位)和花坛的面积(结果保留小数点后一位).例4 ∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO = ∠ABC = × 60°= 30°.
在Rt△OAB中,AO = AB = ×20=10,
∴花坛的两条小路长AC = 2AO =20 (m),
BD = 2BO=20 ≈34. 64 (m).
花坛的面积S四边形ABCD=4×S△OAB
= AC·BD=200 ≈346. 4 (m2).知3-讲解:知3-讲菱形的面积有三种计算方法:
(1)将其看成平行四边形,用底与高的积来求;
(2)对角线分得的四个全等直角三角形面积之和;
(3)两条对角线乘积的一半.
说明:读者可利用(1)(2)两种方法试一试;注意应
用(3)这种方法时不要忽视“一半”.1 已知菱形的两条对角线的长分别是6和8,求菱
形的周长和面积.知3-练2 如图,在菱形ABCD中,对角线AC,BD相交于点
O,AB=5,AC=6,过点D作AC的平行线交BC的
延长线于点E,则△BDE的面积为( )
A.22 B.24 C.48 D.44知3-练知4-导4知识点菱形的对称性 如图,比较菱形的对角线和平行四边形的对角线,
我们发现,菱形的对角线把菱形分成四个全等的直角三
角形,而平行四边形通常只被分成两对全等的三角形.
菱形是轴对称图形,它的对角线所在的直线就是它
的对称轴.知4-导 菱形是轴对称图形,它有两条对称轴. 对
称轴是分别经过两组对角顶点的两条直线.例5 如图①,在菱形ABCD中,E,F分
别是CB,CD上的点,且BE=DF.
(1)求证:AE=AF.
(2)若∠B=60°,点E,F分
别是BC,CD的中点,求证:△AEF为等边三角形.知4-讲(1)要证AE=AF,只需证△AEB≌△AFD,由BE=
DF及菱形的相关性质进行证明即可.(2)如图②,要
证△AEF为等边三角形,由AE=AF知,只需证∠EAF
=60°即可,要证∠EAF=60°,只需证∠1=∠2=
30°即可,这可由菱形及等边三角形相关知识证出.导引:知4-讲(1)∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵BE=DF,
∴△ABE≌△ADF,∴AE=AF.
(2)如图②,连接AC.
∵四边形ABCD是菱形,∴AB=BC.
又∵∠B=60°,∴△ABC为等边三角形.
∴∠BAC=60°.
∵E为BC的中点,∴∠1= ∠BAC=30°.
同理∠2=30°,∴∠EAF=60°.
又∵AE=AF,∴△AEF为等边三角形.证明:知4-讲 菱形的每条对角线把菱形分成两个全等的等腰三
角形(特殊时为两个全等的等边三角形),两条对角线
把菱形分成四个全等的直角三角形.所以有关菱形的
一些证明与计算问题常常与特殊的三角形的有关问题
综合在一起.1 如图,在菱形ABCD中,P是AB上的一个动点(不
与A,B重合),连接DP交对角线AC于点E,连接
EB.求证:∠APD=∠EBC.知4-练2 如图,O是菱形ABCD的对角线AC,BD的交点,E,
F分别是OA,OC的中点,下列结论:①S△ADE=
S△EOD;②四边形BFDE是轴对称图形;③△DEF是
轴对称图形;④∠ADE=∠EDO.其中正确的有( )
A.1个
B.2个
C.3个
D.4个知4-练1.菱形的定义:有一组邻边相等的平行四边形叫做
菱形
2.菱形的性质:
(1)它具有平行四边形的一切性质.
(2)菱形的四条边相等.
(3)菱形的对角线互相垂直, 并且一条对角线平分
一组对角.
菱形的边的性质
菱形的对角线的性质
菱形的对称性2课时流程逐点
导讲练课堂小结作业提升 菱形具有平行四边形的不稳定性,具有变化中
的不变性,有对称美在生活中,被人们广泛地采用,
如图为“中国花边”,其中就有很多菱形的图案.在
我们的周边,还有哪些物体是菱形的形状,用到菱
形的哪些性质?1知识点菱形的定义 我们观察平行四边形的一组邻边,如右图,当
这组邻边相等时,这时的平行四边形也是一个特殊
的平行四边形.有一组邻边相等的平行四边形叫做菱形(rhombus).
菱形也是常见的图形.一些门窗的窗格、美丽的中国结、伸缩
的衣帽架 (下图)等都有菱形的形象.你还能举出一些例子吗? 知1-导知1-讲定义:有一组邻边相等的平行四边形叫做菱形.
要点精析:
(1)菱形必须满足两个条件:一是平行四边形;二是
一组邻边相等.二者必须同时具备,缺一不可.
(2)菱形的定义既是菱形的基本性质,也是菱形的基
本判定方法.例1 已知:如图,在△ABC中,CD平分∠ACB交AB
于点D,DE∥AC交BC于点E,DF∥BC交AC于
点F. 四边形DECF是菱形吗?为什么?知1-讲因为DE∥FC,DF∥EC,所
以四边形DECF为平行四边
形,再根据有一组邻边相等
的平行四边形是菱形求证即
可.导引:知1-讲四边形DECF是菱形.理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD平分∠ACB,
∴∠1=∠2,∴∠1=∠3,∴DE=EC,
∴平行四边形DECF为菱形(有一组邻边相等的平
行四边形是菱形).解:知1-讲 本题考查了菱形的定义,菱形的定义也可
以作为菱形的判定方法.1 〈安顺〉如图,已知点D在△ABC的BC边上,DE
∥AC交AB于E,DF∥AB交AC于F.
(1)证明:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,
并说明理由.知1-练2 如图,若要使平行四边形ABCD成为菱形,则需
要添加的条件是( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD知1-练2知识点菱形的边的性质知2-导 菱形具有平行四边形的所有性质.此外,菱形
还具有哪些特殊性质呢? 根据菱形的轴对称性,你
发现菱形的四条边具有什么大小关系?问 题菱形的四条边都相等.知2-讲例2 如图所示,菱形ABCD中,∠B=60°,AB=2,
E、F分别是BC、CD的中点,连接AE、EF、
AF,则△AEF的周长为( )
A. B.
C. D.3 在菱形ABCD中,因为∠B=60°,连接AC,则
△ABC是等边三角形,又因为E分别是BC的中点,
所以AE垂直于BC,因此AE= ,所以
△AEF的周长为 ,故选B.B分析:知2-讲 在菱形中作辅助线经常连接对角线,构造
三角形来做题,能够迎刃而解.1 边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm C.12 cm D.15 cm
2 (2015·台州)如图,在菱形ABCD中,AB=8,点E,
F分别在AB,AD上,且AE=AF,过点E作EG∥AD
交CD于点G,过点F作FH∥AB交BC于点H,EG与
FH交于点O,当四边形AEOF与四边形CGOH的周长
之差为12时,AE的长为( )
A.6.5 B.6
C.5.5 D.5知2-练知2-练3 如图所示,在菱形ABCD中,AB = 5,∠BCD =?
120°,则对角线AC等于( )
A.20
B.15
C.10
D.53知识点菱形的对角线的性质知3-导 因为菱形是平行四边形,所以它具有平行四边形的
所有性质.由于它的一组邻边相等,它是否具有一般平行
四边形不具有的一些特殊性质呢?思考菱形的两条对角线AC与BD之间具有什么位置关系?知3-导 对于菱形,我们仍然从它的对角线等方面进行研
究.可以发现并证明(请你自己完成证明),菱形还有以
下性质:
菱形的两条对角线互相垂直,并且每一条对角线
平分一组对角.知3-导问 题菱形的面积如何计算呢?菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积
时,要灵活运用使计算简单.由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直平分,因此可以在直角
三角形中利用勾股定理来进行计算.知3-讲例3 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=12 cm,AC=6 cm.求菱形的周长.导引:∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,由勾股定理,
得AB=
∴菱形的周长=4AB知3-讲解:知3-讲 菱形的对角线将菱形分成四个全等的直角三角
形,我们通常将菱形问题中求相关线段的长转化为
求直角三角形中相关线段的长,再利用勾股定理来
计算.1 如图,四边形ABCD是菱形,BE⊥AD,BF⊥CD,
垂足分别为E,F.
(1)求证:BE=BF;
(2)当菱形ABCD的对角线AC=8,BD=6时,
求BE的长.知3-练2 (2016·枣庄)如图,四边形ABCD是菱形,AC=8,
DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4知3-练知3-讲如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小
路AC和BD. 求两条小路的长(结果保留小数点后
两位)和花坛的面积(结果保留小数点后一位).例4 ∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO = ∠ABC = × 60°= 30°.
在Rt△OAB中,AO = AB = ×20=10,
∴花坛的两条小路长AC = 2AO =20 (m),
BD = 2BO=20 ≈34. 64 (m).
花坛的面积S四边形ABCD=4×S△OAB
= AC·BD=200 ≈346. 4 (m2).知3-讲解:知3-讲菱形的面积有三种计算方法:
(1)将其看成平行四边形,用底与高的积来求;
(2)对角线分得的四个全等直角三角形面积之和;
(3)两条对角线乘积的一半.
说明:读者可利用(1)(2)两种方法试一试;注意应
用(3)这种方法时不要忽视“一半”.1 已知菱形的两条对角线的长分别是6和8,求菱
形的周长和面积.知3-练2 如图,在菱形ABCD中,对角线AC,BD相交于点
O,AB=5,AC=6,过点D作AC的平行线交BC的
延长线于点E,则△BDE的面积为( )
A.22 B.24 C.48 D.44知3-练知4-导4知识点菱形的对称性 如图,比较菱形的对角线和平行四边形的对角线,
我们发现,菱形的对角线把菱形分成四个全等的直角三
角形,而平行四边形通常只被分成两对全等的三角形.
菱形是轴对称图形,它的对角线所在的直线就是它
的对称轴.知4-导 菱形是轴对称图形,它有两条对称轴. 对
称轴是分别经过两组对角顶点的两条直线.例5 如图①,在菱形ABCD中,E,F分
别是CB,CD上的点,且BE=DF.
(1)求证:AE=AF.
(2)若∠B=60°,点E,F分
别是BC,CD的中点,求证:△AEF为等边三角形.知4-讲(1)要证AE=AF,只需证△AEB≌△AFD,由BE=
DF及菱形的相关性质进行证明即可.(2)如图②,要
证△AEF为等边三角形,由AE=AF知,只需证∠EAF
=60°即可,要证∠EAF=60°,只需证∠1=∠2=
30°即可,这可由菱形及等边三角形相关知识证出.导引:知4-讲(1)∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵BE=DF,
∴△ABE≌△ADF,∴AE=AF.
(2)如图②,连接AC.
∵四边形ABCD是菱形,∴AB=BC.
又∵∠B=60°,∴△ABC为等边三角形.
∴∠BAC=60°.
∵E为BC的中点,∴∠1= ∠BAC=30°.
同理∠2=30°,∴∠EAF=60°.
又∵AE=AF,∴△AEF为等边三角形.证明:知4-讲 菱形的每条对角线把菱形分成两个全等的等腰三
角形(特殊时为两个全等的等边三角形),两条对角线
把菱形分成四个全等的直角三角形.所以有关菱形的
一些证明与计算问题常常与特殊的三角形的有关问题
综合在一起.1 如图,在菱形ABCD中,P是AB上的一个动点(不
与A,B重合),连接DP交对角线AC于点E,连接
EB.求证:∠APD=∠EBC.知4-练2 如图,O是菱形ABCD的对角线AC,BD的交点,E,
F分别是OA,OC的中点,下列结论:①S△ADE=
S△EOD;②四边形BFDE是轴对称图形;③△DEF是
轴对称图形;④∠ADE=∠EDO.其中正确的有( )
A.1个
B.2个
C.3个
D.4个知4-练1.菱形的定义:有一组邻边相等的平行四边形叫做
菱形
2.菱形的性质:
(1)它具有平行四边形的一切性质.
(2)菱形的四条边相等.
(3)菱形的对角线互相垂直, 并且一条对角线平分
一组对角.
