18.2.6 正方形的判定课件
图片预览







文档简介
课件26张PPT。第十八章 平行四边形18.2 特殊的平行四边形第3课时 正方形的判定1课堂讲解正方形面积的性质
正方形的判定2课时流程逐点
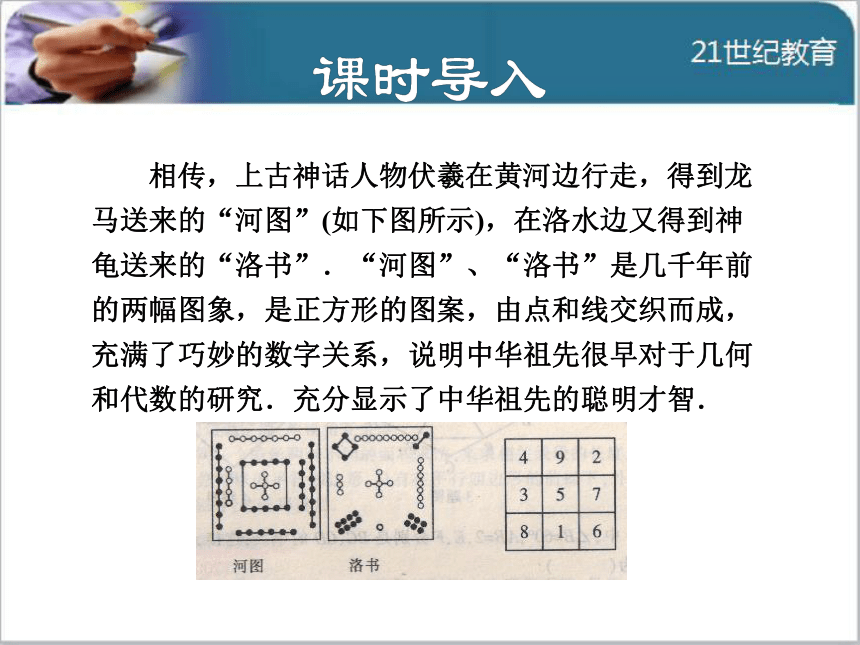
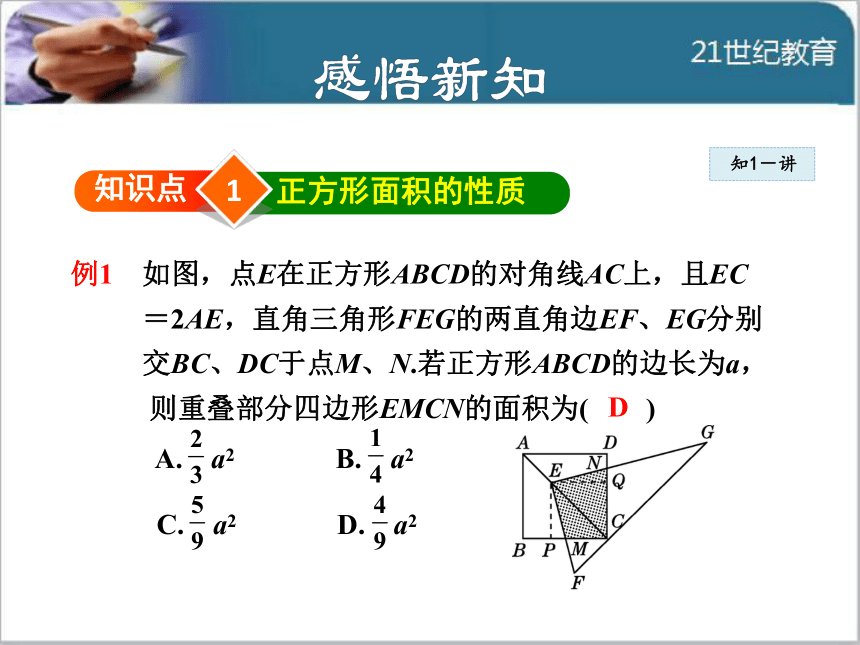
导讲练课堂小结作业提升 相传,上古神话人物伏羲在黄河边行走,得到龙马送来的“河图”(如下图所示),在洛水边又得到神龟送来的“洛书”.“河图”、“洛书”是几千年前的两幅图象,是正方形的图案,由点和线交织而成,充满了巧妙的数字关系,说明中华祖先很早对于几何和代数的研究.充分显示了中华祖先的聪明才智.1知识点正方形面积的性质例1 如图,点E在正方形ABCD的对角线AC上,且EC
=2AE,直角三角形FEG的两直角边EF、EG分别
交BC、DC于点M、N.若正方形ABCD的边长为a,
则重叠部分四边形EMCN的面积为( )
A. a2 B. a2
C. a2 D. a2知1-讲D作EP⊥BC于点P,EQ⊥CD于点Q,易得△EPM
≌△EQN,利用四边形EMCN的面积等于正方形
PCQE的面积求解.
作EP⊥BC于点P,EQ⊥CD于点Q,
∵四边形ABCD是正方形,∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG是直角三角形,∴∠NEF=∠NEQ+
∠MEQ=90°,∴∠PEM=∠NEQ,
∵CA是∠BCD的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形,知1-讲导引:
在△EPM和△EQN中,
∴△EPM≌△EQN(ASA),∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积,
∵正方形ABCD的边长为a,∴AC= a,
∵EC=2AE,∴EC= a,∴EP=PC= a,
∴正方形PCQE的面积= a× a= a2,
∴四边形EMCN的面积= a2.知1-讲知1-讲 本例解法在于巧用割补法,将分散的图形拼合在
一起,将不规则的阴影面积集中到一个规则的图形中,
再利用正方形及三角形的性质求出,解答过程体现了
割补法及转化思想.1 〈枣庄〉如图,边长为1的正方形ABCD绕点A逆
时针旋转45°得到正方形 AB1C1D1,边 B1C1与
CD交于点O,则四边形AB1OD的面积是( )
A. B. C. D. -1知1-练2 如图,正方形ABCD的边长为2,H在CD的延长线
上,四边形CEFH也为正方形,则△DBF的面积
为( )
A.4 B. C.2 D.2知1-练2知识点正方形的判定知2-导 正方形有哪些性质?如何判定一个四边形是正方
形?把它们写出来,并和同学交流一下,然后证明其
中的一些结论.思考知2-导 我们学习了平行四边形、矩形、菱形、正方形,
那么思考一下,它们之间有怎样的包含关系?问题知2-讲正方形的判定方法:
要判定一个四边形是正方形,最常用的方法就是
先证明它是矩形(或菱形),再证明这个矩形(或菱形)有
一组邻边相等(或有一个角是直角),其实质就是根据正
方形的定义来判定,当然也可以先证四边形是平行四
边形,再证有一组邻边相等且有一个角是直角,或证
这个平行四边形的对角线相等并且互相垂直.知2-讲例2 如图,在△ABC中,∠ACB=90°,CD平分
∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,
F. 求证:四边形CFDE是正方形.要证四边形CFDE是正方形,
首先要确定这个正方形建立
在哪种四边形的基础上,即
先证它是什么四边形;再证
这种四边形是正方形需要补
充的条件.导引:知2-讲证法一:∵DE⊥BC,AC⊥BC,∴DE∥CF.
同理DF∥CE,
∴四边形CFDE是平行四边形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴? CFDE是菱形.
∵∠ACB=90°,∴菱形CFDE是正方形.
证法二:∵∠ECF=∠CFD=∠CED=90°,
∴四边形CFDE是矩形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴矩形CFDE是正方形.知2-讲 证明条件中不含对角线的四边形是正方形的四种
方法:方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直
角”;方法3:证:“矩形+一组邻边相等”;方法4:
证:“菱形+一个直角”.
说明:在判定四边形是正方形时,四边形常常是
建立在矩形或菱形的基础上,采用方法3、方法4进行
证明;如证明中的证法一、证法二;本例也可采用方
法1、方法2,请读者去试一试.1 已知:如图,点M是矩形ABCD的边AD的中点,点
P是BC边上的一动点,PE⊥CM,PF⊥BM,垂足
分别为E、F.
(1)当矩形ABCD的长与宽满足
什么条件时,四边形PEMF
为矩形?试说明理由;
(2)在(1)中,当点P运动到什么位置时,矩形PEMF
为正方形?为什么?知2-练2 下列选项中不能判定四边形ABCD是正方形(对角
线交于点O)的是( )
A.AB CD,AB=AD,∠BAD=90°
B.AB=BC=CD=AD,∠ABC=90°
C.∠BAD=∠ABC=∠BCD=90°,AC=BD
D.AO=CO=BO=DO,AC⊥BD知2-练知2-讲例3 如图,已知在?ABCD中,对角线AC,BD交于点O,E
是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,
求证:四边形ABCD是正方形.要证?ABCD是正方形,有三种途径可走:即在平行四
边形、菱形、矩形的基础上,找各需补充的对角线的
条件进行证明;若要证明?ABCD是菱形,由于题中条
件与对角线相关,则需证AC⊥BD.导引:知2-讲(1)首先根据平行四边形的性质可得AO=CO,再由EA
=EC可得△EAC是等腰三角形,然后根据等腰三角
形三线合一的性质可得EO⊥AC,根据对角线互相
垂直的平行四边形是菱形可证出结论;
(2)首先根据角的关系得出AO=DO,进而得到AC=
BD,再根据对角线相等的菱形是正方形可得到结
论.知2-讲 (1)∵四边形ABCD是平行四边形,∴AO=CO,
∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD是菱形,
∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD是正方形.证明:知2-讲 证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
证明一个四边形是正方形的方法:需结合条件选
择合理的判定方法,一般先证明是矩形,然后找出一
组邻边相等或对角线互相垂直;或者先证明是菱形,
然后找一个角是直角或对角线相等.1 如图,已知?ABCD中,对角线AC,BD交于点O,
E是BD延长线上的点,且△ACE是等边三角形,
若∠AED=2∠EAD.
求证:四边形ABCD是正方形.知2-练2 (2016·益阳)下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形知2-练3 (2015·日照)小明在学习了正方形之后,给同桌小文
出了道题,从下列四个条件:①AB=BC;②∠ABC
=90°;③AC=BD;④AC⊥BD中选两个作为补充
条件,使?ABCD为正方形(如图),现有下列四种选法,
你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④知2-练 证明条件中不含对角线的四边形是正方形的四
种方法:
方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直
角”;
方法3:证:“矩形+一组邻边相等”;
方法4:证:“菱形+一个直角”. 证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
正方形的判定2课时流程逐点
导讲练课堂小结作业提升 相传,上古神话人物伏羲在黄河边行走,得到龙马送来的“河图”(如下图所示),在洛水边又得到神龟送来的“洛书”.“河图”、“洛书”是几千年前的两幅图象,是正方形的图案,由点和线交织而成,充满了巧妙的数字关系,说明中华祖先很早对于几何和代数的研究.充分显示了中华祖先的聪明才智.1知识点正方形面积的性质例1 如图,点E在正方形ABCD的对角线AC上,且EC
=2AE,直角三角形FEG的两直角边EF、EG分别
交BC、DC于点M、N.若正方形ABCD的边长为a,
则重叠部分四边形EMCN的面积为( )
A. a2 B. a2
C. a2 D. a2知1-讲D作EP⊥BC于点P,EQ⊥CD于点Q,易得△EPM
≌△EQN,利用四边形EMCN的面积等于正方形
PCQE的面积求解.
作EP⊥BC于点P,EQ⊥CD于点Q,
∵四边形ABCD是正方形,∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG是直角三角形,∴∠NEF=∠NEQ+
∠MEQ=90°,∴∠PEM=∠NEQ,
∵CA是∠BCD的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形,知1-讲导引:
在△EPM和△EQN中,
∴△EPM≌△EQN(ASA),∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积,
∵正方形ABCD的边长为a,∴AC= a,
∵EC=2AE,∴EC= a,∴EP=PC= a,
∴正方形PCQE的面积= a× a= a2,
∴四边形EMCN的面积= a2.知1-讲知1-讲 本例解法在于巧用割补法,将分散的图形拼合在
一起,将不规则的阴影面积集中到一个规则的图形中,
再利用正方形及三角形的性质求出,解答过程体现了
割补法及转化思想.1 〈枣庄〉如图,边长为1的正方形ABCD绕点A逆
时针旋转45°得到正方形 AB1C1D1,边 B1C1与
CD交于点O,则四边形AB1OD的面积是( )
A. B. C. D. -1知1-练2 如图,正方形ABCD的边长为2,H在CD的延长线
上,四边形CEFH也为正方形,则△DBF的面积
为( )
A.4 B. C.2 D.2知1-练2知识点正方形的判定知2-导 正方形有哪些性质?如何判定一个四边形是正方
形?把它们写出来,并和同学交流一下,然后证明其
中的一些结论.思考知2-导 我们学习了平行四边形、矩形、菱形、正方形,
那么思考一下,它们之间有怎样的包含关系?问题知2-讲正方形的判定方法:
要判定一个四边形是正方形,最常用的方法就是
先证明它是矩形(或菱形),再证明这个矩形(或菱形)有
一组邻边相等(或有一个角是直角),其实质就是根据正
方形的定义来判定,当然也可以先证四边形是平行四
边形,再证有一组邻边相等且有一个角是直角,或证
这个平行四边形的对角线相等并且互相垂直.知2-讲例2 如图,在△ABC中,∠ACB=90°,CD平分
∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,
F. 求证:四边形CFDE是正方形.要证四边形CFDE是正方形,
首先要确定这个正方形建立
在哪种四边形的基础上,即
先证它是什么四边形;再证
这种四边形是正方形需要补
充的条件.导引:知2-讲证法一:∵DE⊥BC,AC⊥BC,∴DE∥CF.
同理DF∥CE,
∴四边形CFDE是平行四边形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴? CFDE是菱形.
∵∠ACB=90°,∴菱形CFDE是正方形.
证法二:∵∠ECF=∠CFD=∠CED=90°,
∴四边形CFDE是矩形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴矩形CFDE是正方形.知2-讲 证明条件中不含对角线的四边形是正方形的四种
方法:方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直
角”;方法3:证:“矩形+一组邻边相等”;方法4:
证:“菱形+一个直角”.
说明:在判定四边形是正方形时,四边形常常是
建立在矩形或菱形的基础上,采用方法3、方法4进行
证明;如证明中的证法一、证法二;本例也可采用方
法1、方法2,请读者去试一试.1 已知:如图,点M是矩形ABCD的边AD的中点,点
P是BC边上的一动点,PE⊥CM,PF⊥BM,垂足
分别为E、F.
(1)当矩形ABCD的长与宽满足
什么条件时,四边形PEMF
为矩形?试说明理由;
(2)在(1)中,当点P运动到什么位置时,矩形PEMF
为正方形?为什么?知2-练2 下列选项中不能判定四边形ABCD是正方形(对角
线交于点O)的是( )
A.AB CD,AB=AD,∠BAD=90°
B.AB=BC=CD=AD,∠ABC=90°
C.∠BAD=∠ABC=∠BCD=90°,AC=BD
D.AO=CO=BO=DO,AC⊥BD知2-练知2-讲例3 如图,已知在?ABCD中,对角线AC,BD交于点O,E
是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,
求证:四边形ABCD是正方形.要证?ABCD是正方形,有三种途径可走:即在平行四
边形、菱形、矩形的基础上,找各需补充的对角线的
条件进行证明;若要证明?ABCD是菱形,由于题中条
件与对角线相关,则需证AC⊥BD.导引:知2-讲(1)首先根据平行四边形的性质可得AO=CO,再由EA
=EC可得△EAC是等腰三角形,然后根据等腰三角
形三线合一的性质可得EO⊥AC,根据对角线互相
垂直的平行四边形是菱形可证出结论;
(2)首先根据角的关系得出AO=DO,进而得到AC=
BD,再根据对角线相等的菱形是正方形可得到结
论.知2-讲 (1)∵四边形ABCD是平行四边形,∴AO=CO,
∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD是菱形,
∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD是正方形.证明:知2-讲 证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
证明一个四边形是正方形的方法:需结合条件选
择合理的判定方法,一般先证明是矩形,然后找出一
组邻边相等或对角线互相垂直;或者先证明是菱形,
然后找一个角是直角或对角线相等.1 如图,已知?ABCD中,对角线AC,BD交于点O,
E是BD延长线上的点,且△ACE是等边三角形,
若∠AED=2∠EAD.
求证:四边形ABCD是正方形.知2-练2 (2016·益阳)下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形知2-练3 (2015·日照)小明在学习了正方形之后,给同桌小文
出了道题,从下列四个条件:①AB=BC;②∠ABC
=90°;③AC=BD;④AC⊥BD中选两个作为补充
条件,使?ABCD为正方形(如图),现有下列四种选法,
你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④知2-练 证明条件中不含对角线的四边形是正方形的四
种方法:
方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直
角”;
方法3:证:“矩形+一组邻边相等”;
方法4:证:“菱形+一个直角”. 证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
