19.1.2 函数课件
图片预览







文档简介
课件24张PPT。第2课时 函 数第十九章 一次函数19.1 函 数1课堂讲解函数的定义
自变量的取值范围
函数值2课时流程逐点
导讲练课堂小结作业提升 根据经验,跳远的距
离 s=0.085v2(v是助跑的
速度,0<v<10.5米/秒),
其中变量s随着哪一个量
的变化而变化?1知识点函数的定义知1-导思考
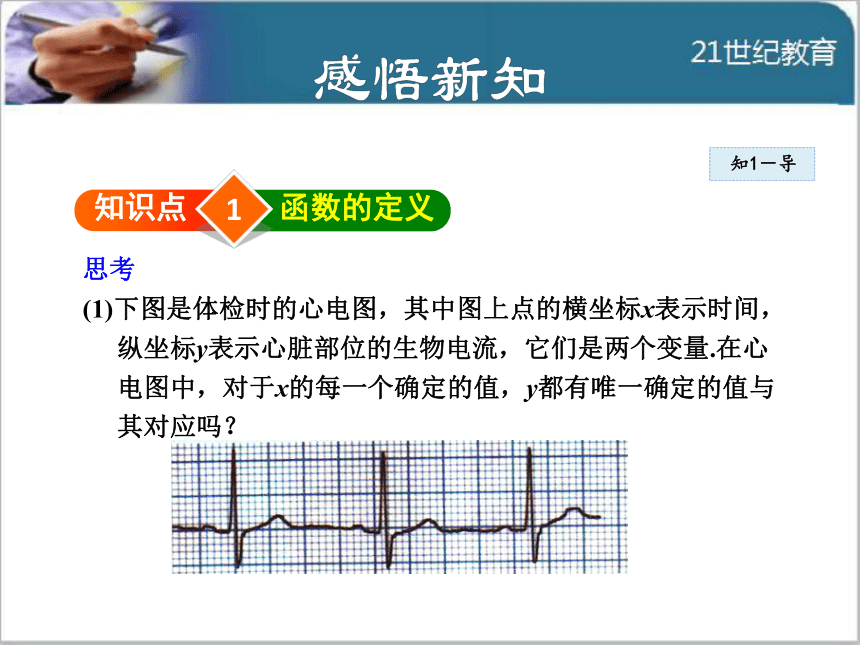
(1)下图是体检时的心电图,其中图上点的横坐标x表示时间,
纵坐标y表示心脏部位的生物电流,它们是两个变量.在心
电图中,对于x的每一个确定的值,y都有唯一确定的值与
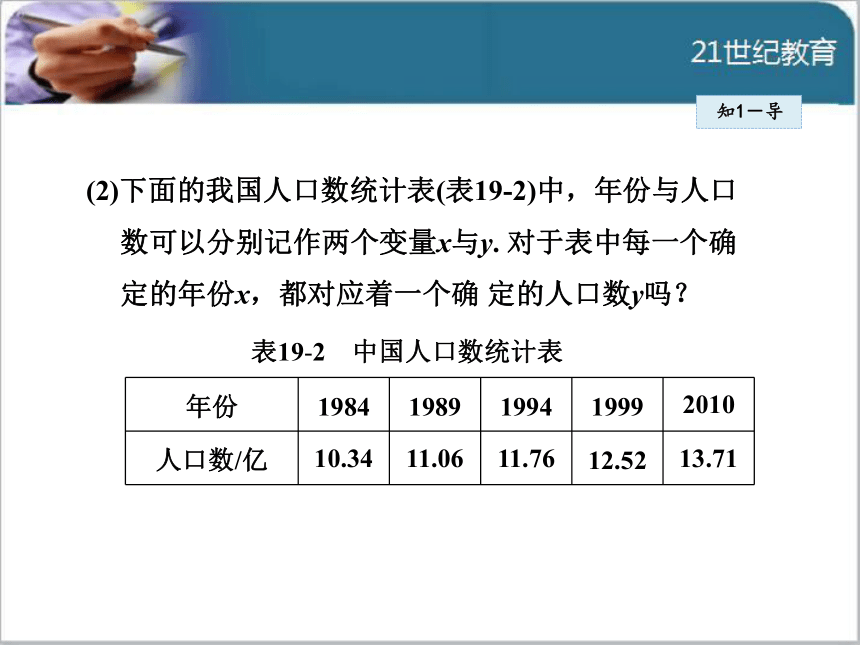
其对应吗? 知1-导(2)下面的我国人口数统计表(表19-2)中,年份与人口
数可以分别记作两个变量x与y. 对于表中每一个确
定的年份x,都对应着一个确 定的人口数y吗?表19-2 中国人口数统计表 一般地,在一个变化过程中,如果有两个变量
x与y,并且对于x的每一个确定的值,y都有唯一确
定的值与其对应,那么我们就说x是自变量,y是x
的函数.知1-导知1-讲函数:一般地,在一个变化过程中,如果有两个变量
x和y,并且对于x的每一个确定的值,y都有唯一确定
的值与其对应,那么我们就说x是自变量,y是x的函数.
要点精析:理解函数的定义应注意以下三点(简称函数
“三要素”):
(1)有两个变量;
(2)一个变量的数值随着另一个变量数值的变化而变化;
(3)对于自变量的每一个确定的值,函数有且只有一个
值与之对应.知1-讲例1 紧扣函数的定义,要判断y是不是x的函数,关键看
给x一个值,y是否也有一个唯一的值与其对应.若
是,则y就是x的函数;若不是,则y就不是x的函数.导引:如图,各曲线中表示y是x的函数的是________
(写出所有满足条件的图的序号).①②③判断一个关系是否是函数关系的方法:一看是否存在
于一个变化过程中;二看过程中是否存在两个变量;
三看对于一个变量每取一个确定的值,另一个变量是
否都有唯一确定的值与之对应.三者必须同时满足.
解本例的技巧在于过x轴上任意一点作x轴的垂线,若
垂线与图象交于两点或多点,说明x取一值,有两个
或多个y与其对应,则y不是x的函数.它是以形来表
达函数关系.知1-讲知1-练1 下列各式中,是函数的是( )
A.y=4x-3 B.x-4=8
C.x2+2y=6y2 D.x+4y
2 下面每个选项中给出了某个变化过程中的两个变量
x和y,其中y不是x的函数的是( )
A.y:正方形的面积,x:这个正方形的周长
B.y:菱形的周长,x:这个菱形的边长
C.y:圆的面积,x:这个圆的直径
D.y:一个正数的平方根,x:这个正数2知识点自变量的取值范围知2-讲例2 (1)函数 中,自变量x的取值范围是________.
(2)下列函数中,自变量x的取值范围是x>2的函数是( )
A. B.
C. D.x≠-1C对于第(1)题,易从1+x≠0,得x≠-1;
对于第(2)小题分别确定A、B、C、D的取值范围,
可知只有C的取值范围是x>2.导引: 自变量的取值范围要使所给函数解析式有意义,
而实际问题中的自变量取值,还应保证实际问题有
意义.知2-讲1 函数 中自变量x的取值范围是( )
A.x>3 B.x<3
C.x≠3 D.x≠-3
2 (2016·无锡)函数 中自变量x的取值范围是
( )
A.x>2 B.x≥2
C.x≤2 D.x≠2知2-练3 (2015·广安)如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为( )
A.y=x+2 B.y=x2+2
C.y= D.y= 知2-练3知识点函数值知3-导 一般地,在一个变化过程中,如果有两个变量x与y,
并且对于x的每一个确定的值,y都有唯一确定的值与其对
应,那么我们就说x是自变量,y是x的函数. 如果当x=a时y
=b,那么b叫做当自变量的值为a时的函数值.
可以认为:在前面问题(1)中,时间t是自变量,路程s
是t的函数,当t=1时,函数值s=60,当t=2时,函数值s=
120;在心电图中,时间x是自变量,心脏部位的生物电流y
是x的函数;在人口数统计表中,年份x是自变量,人口数y
是x的函数,当x=2010时,函数值y=13. 71.知3-讲函数值:如果在自变量取值范围内给定一个数值a,
函数对应的值为b,那么b叫做自变量的值为a时的
函数值.
要点精析:
(1)函数表示的是两个变量之间的一种关系,而函数
值是一个数值.
(2)一个函数的函数值是随着自变量的变化而变化的,
故在求函数值时,一定要指明自变量为多少时的
函数值.知3-讲例3 汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3) 汽车行驶200 km时,油箱中还有多少汽油?(1)行驶路程x是自变量,油箱中的油量y是x的函数,
它们的关系为y= 50-0.1x.解:知3-讲(2)仅从式子y=50-0.1x看,x可以取任意实数.但是考
虑到x代表的实际意义为行驶路程,因此x不能取负
数.行驶中的耗油量为0.1x,它不能超过油箱中现有
汽油量50,即0. 1x≤50.
因此,自变量x的取值范围是0≤ x≤500.知3-讲(3)汽车行驶200 km时,油箱中的汽油量是函数
y=50-0.1x在x=200时的函数值.将x=200 代入
y=50-0.1x,得y=50-0.1×200=30.
汽车行驶200 km时,油箱中还有30 L汽油. 求函数值时,要注意函数的对应关系,代入自
变量的值计算时,要按照函数中代数式指明的运算
顺序计算,并结合相应的运算法则,使运算简便;
说函数值时,要说明自变量是多少时的函数值.知3-讲知3-练1 已知等腰三角形的周长是20.
(1)求腰长y与底边长x之间的函数关系式;
(2)求自变量x的取值范围;
(3)求当x=8时的函数值.
2 下列关系式中,当自变量x=-1时,函数值y=6
的是( )
A.y=3x+3 B.y=-3x+3
C.y=3x-3 D.y=-3x-3知3-练3 (2015·百色)已知函数 当x=2时,
函数值y为( )
A.5 B.6 C.7 D.81.判断变量之间具有函数关系的三个要素:
(1)一个变化过程;
(2)有两个变量;
(3)一个变量的值确定后,另一个变量就有唯一确
定的值和它对应.2.确定自变量的取值范围的方法:
(1)整式和奇次根式中,自变量的取值范围是全体
实数;
(2)偶次根式中,被开方式大于或等于0;
(3)分式中,分母不能为0;
(4)零指数幂、负整数指数幂中,底数不为0;
(5)实际问题中,自变量除了满足解析式有意义外,
还要考虑使实际问题有意义.
自变量的取值范围
函数值2课时流程逐点
导讲练课堂小结作业提升 根据经验,跳远的距
离 s=0.085v2(v是助跑的
速度,0<v<10.5米/秒),
其中变量s随着哪一个量
的变化而变化?1知识点函数的定义知1-导思考
(1)下图是体检时的心电图,其中图上点的横坐标x表示时间,
纵坐标y表示心脏部位的生物电流,它们是两个变量.在心
电图中,对于x的每一个确定的值,y都有唯一确定的值与
其对应吗? 知1-导(2)下面的我国人口数统计表(表19-2)中,年份与人口
数可以分别记作两个变量x与y. 对于表中每一个确
定的年份x,都对应着一个确 定的人口数y吗?表19-2 中国人口数统计表 一般地,在一个变化过程中,如果有两个变量
x与y,并且对于x的每一个确定的值,y都有唯一确
定的值与其对应,那么我们就说x是自变量,y是x
的函数.知1-导知1-讲函数:一般地,在一个变化过程中,如果有两个变量
x和y,并且对于x的每一个确定的值,y都有唯一确定
的值与其对应,那么我们就说x是自变量,y是x的函数.
要点精析:理解函数的定义应注意以下三点(简称函数
“三要素”):
(1)有两个变量;
(2)一个变量的数值随着另一个变量数值的变化而变化;
(3)对于自变量的每一个确定的值,函数有且只有一个
值与之对应.知1-讲例1 紧扣函数的定义,要判断y是不是x的函数,关键看
给x一个值,y是否也有一个唯一的值与其对应.若
是,则y就是x的函数;若不是,则y就不是x的函数.导引:如图,各曲线中表示y是x的函数的是________
(写出所有满足条件的图的序号).①②③判断一个关系是否是函数关系的方法:一看是否存在
于一个变化过程中;二看过程中是否存在两个变量;
三看对于一个变量每取一个确定的值,另一个变量是
否都有唯一确定的值与之对应.三者必须同时满足.
解本例的技巧在于过x轴上任意一点作x轴的垂线,若
垂线与图象交于两点或多点,说明x取一值,有两个
或多个y与其对应,则y不是x的函数.它是以形来表
达函数关系.知1-讲知1-练1 下列各式中,是函数的是( )
A.y=4x-3 B.x-4=8
C.x2+2y=6y2 D.x+4y
2 下面每个选项中给出了某个变化过程中的两个变量
x和y,其中y不是x的函数的是( )
A.y:正方形的面积,x:这个正方形的周长
B.y:菱形的周长,x:这个菱形的边长
C.y:圆的面积,x:这个圆的直径
D.y:一个正数的平方根,x:这个正数2知识点自变量的取值范围知2-讲例2 (1)函数 中,自变量x的取值范围是________.
(2)下列函数中,自变量x的取值范围是x>2的函数是( )
A. B.
C. D.x≠-1C对于第(1)题,易从1+x≠0,得x≠-1;
对于第(2)小题分别确定A、B、C、D的取值范围,
可知只有C的取值范围是x>2.导引: 自变量的取值范围要使所给函数解析式有意义,
而实际问题中的自变量取值,还应保证实际问题有
意义.知2-讲1 函数 中自变量x的取值范围是( )
A.x>3 B.x<3
C.x≠3 D.x≠-3
2 (2016·无锡)函数 中自变量x的取值范围是
( )
A.x>2 B.x≥2
C.x≤2 D.x≠2知2-练3 (2015·广安)如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为( )
A.y=x+2 B.y=x2+2
C.y= D.y= 知2-练3知识点函数值知3-导 一般地,在一个变化过程中,如果有两个变量x与y,
并且对于x的每一个确定的值,y都有唯一确定的值与其对
应,那么我们就说x是自变量,y是x的函数. 如果当x=a时y
=b,那么b叫做当自变量的值为a时的函数值.
可以认为:在前面问题(1)中,时间t是自变量,路程s
是t的函数,当t=1时,函数值s=60,当t=2时,函数值s=
120;在心电图中,时间x是自变量,心脏部位的生物电流y
是x的函数;在人口数统计表中,年份x是自变量,人口数y
是x的函数,当x=2010时,函数值y=13. 71.知3-讲函数值:如果在自变量取值范围内给定一个数值a,
函数对应的值为b,那么b叫做自变量的值为a时的
函数值.
要点精析:
(1)函数表示的是两个变量之间的一种关系,而函数
值是一个数值.
(2)一个函数的函数值是随着自变量的变化而变化的,
故在求函数值时,一定要指明自变量为多少时的
函数值.知3-讲例3 汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3) 汽车行驶200 km时,油箱中还有多少汽油?(1)行驶路程x是自变量,油箱中的油量y是x的函数,
它们的关系为y= 50-0.1x.解:知3-讲(2)仅从式子y=50-0.1x看,x可以取任意实数.但是考
虑到x代表的实际意义为行驶路程,因此x不能取负
数.行驶中的耗油量为0.1x,它不能超过油箱中现有
汽油量50,即0. 1x≤50.
因此,自变量x的取值范围是0≤ x≤500.知3-讲(3)汽车行驶200 km时,油箱中的汽油量是函数
y=50-0.1x在x=200时的函数值.将x=200 代入
y=50-0.1x,得y=50-0.1×200=30.
汽车行驶200 km时,油箱中还有30 L汽油. 求函数值时,要注意函数的对应关系,代入自
变量的值计算时,要按照函数中代数式指明的运算
顺序计算,并结合相应的运算法则,使运算简便;
说函数值时,要说明自变量是多少时的函数值.知3-讲知3-练1 已知等腰三角形的周长是20.
(1)求腰长y与底边长x之间的函数关系式;
(2)求自变量x的取值范围;
(3)求当x=8时的函数值.
2 下列关系式中,当自变量x=-1时,函数值y=6
的是( )
A.y=3x+3 B.y=-3x+3
C.y=3x-3 D.y=-3x-3知3-练3 (2015·百色)已知函数 当x=2时,
函数值y为( )
A.5 B.6 C.7 D.81.判断变量之间具有函数关系的三个要素:
(1)一个变化过程;
(2)有两个变量;
(3)一个变量的值确定后,另一个变量就有唯一确
定的值和它对应.2.确定自变量的取值范围的方法:
(1)整式和奇次根式中,自变量的取值范围是全体
实数;
(2)偶次根式中,被开方式大于或等于0;
(3)分式中,分母不能为0;
(4)零指数幂、负整数指数幂中,底数不为0;
(5)实际问题中,自变量除了满足解析式有意义外,
还要考虑使实际问题有意义.
