19.1.4 函数的表示法课件
图片预览






文档简介
课件24张PPT。第4课时 函数的表示法第十九章 一次函数19.1 函 数1课堂讲解函数的表示法
三种函数表示法间的关系2课时流程逐点
导讲练课堂小结作业提升某公司招聘
条件:初中学历以上,团员优先,能吃苦耐劳
年舲:16-25岁
待遇:按钟点计酬(工资标准为每小时8元)
假如你是初中毕业生被聘用,设工作时数为t(时),应得
工资额为m(元),则m=8t.
取一些不同的t的值,求出相应的m的值:
t= 2 时,m= 16 元;t= 3 时,m= 24 元;
…….
在根据不同的工作时数计算你应得工资额的过程中你
用了函数的哪些表示方法呢?1知识点函数的表示法知1-讲函数的表示方法有三种:(1)解析式法;(2)列表法;
(3)图象法.用来表达函数关系的数学式子叫做函数解
析式或函数关系式.用关于自变量的数学式子表示函
数与自变量的方法叫做解析式法. 用表格表示函数关
系的方法,叫做列表法. 用图象表示函数关系的方法.
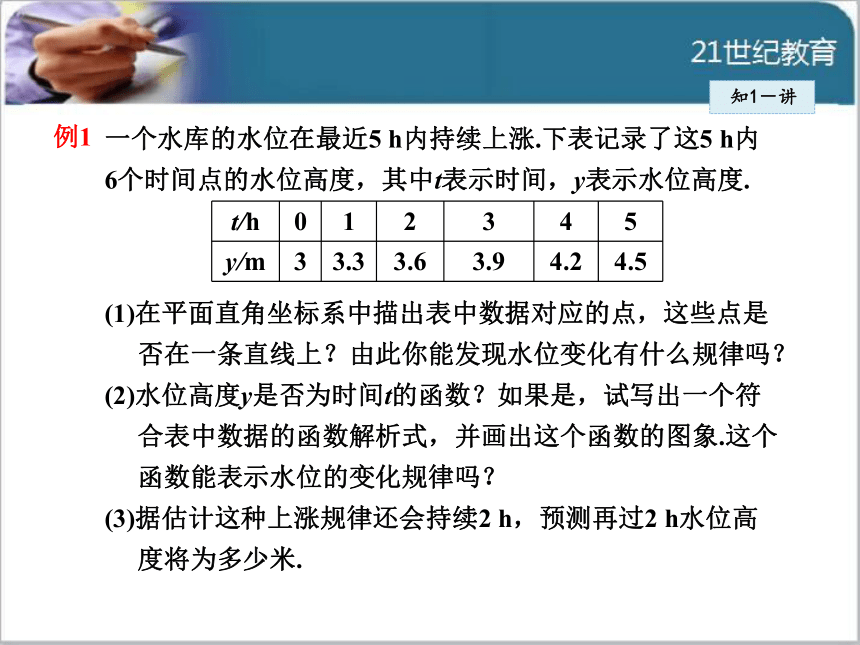
叫做图象法.知1-讲例1 一个水库的水位在最近5 h内持续上涨.下表记录了这5 h内6个时间点的水位高度,其中t表示时间,y表示水位高度.(1)在平面直角坐标系中描出表中数据对应的点,这些点是
否在一条直线上?由此你能发现水位变化有什么规律吗?
(2)水位高度y是否为时间t的函数?如果是,试写出一个符
合表中数据的函数解析式,并画出这个函数的图象.这个
函数能表示水位的变化规律吗?
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高
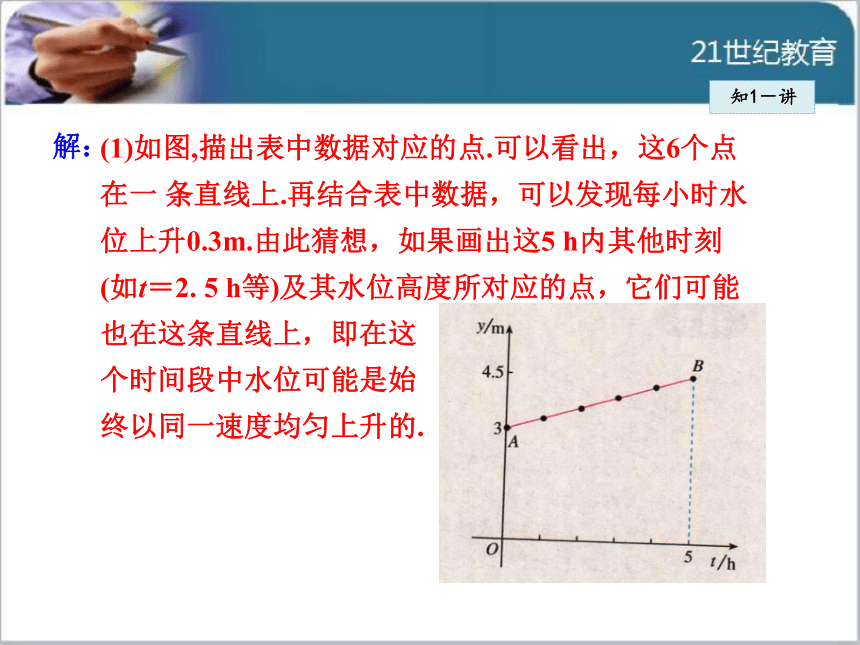
度将为多少米.知1-讲(1)如图,描出表中数据对应的点.可以看出,这6个点
在一 条直线上.再结合表中数据,可以发现每小时水
位上升0.3m.由此猜想,如果画出这5 h内其他时刻
(如t=2. 5 h等)及其水位高度所对应的点,它们可能
也在这条直线上,即在这
个时间段中水位可能是始
终以同一速度均匀上升的.解:知1-讲(2) 由于水位在最近5 h内持续上涨,对于时间 t的每一个确定
的值,水位高度 y都有唯一的值与其对应,所以y是t的函
数.开始时水位高度为3 m,以后每小时水位上升0.3 m.函
数y=0. 3t+3(0≤t≤5)是符合表中数据的一个函数,它表
示经过t h水位上升0.3t m,即水位y为(0. 3t+3)m.其图象是
(1)图中点A(0, 3) 和点B(5, 4.5)之间的线段AB.
如果在这5 h内,水位一直匀速上升, 即升速为0.3m/h,
那么函数y=0.3t+3(0≤t≤5)就精确地表示了这种变化规律.
即使在这5 h内,水位的升速有些变化,而由于每小时水位
上升0.3 m是确定的,因此这个函数也可以近似地表示水位
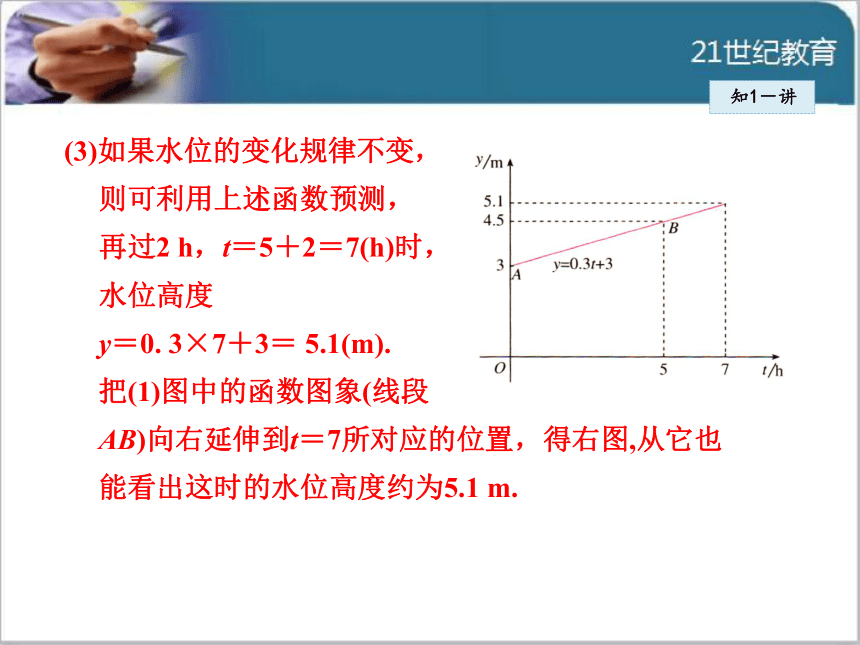
的变化规律.知1-讲(3)如果水位的变化规律不变,
则可利用上述函数预测,
再过2 h,t=5+2=7(h)时,
水位高度
y=0. 3×7+3= 5.1(m).
把(1)图中的函数图象(线段
AB)向右延伸到t=7所对应的位置,得右图,从它也
能看出这时的水位高度约为5.1 m.(1)从图中获取信息首先要弄清楚横、纵轴分别表示
什么意义,再对问题进行分析.
(2)在实际问题中,有的横轴和纵轴上的单位长度可
以不一致,这对问题的结论没有影响,但每条坐
标轴上的单位长度必须要一致.知1-讲知1-练1 某商品原价为560元,随着不同幅度的降价,日销量(件)发生相应的变化,如下表:
这个表反映了________个变量之间的关系,________是自变量,______是函数.从表中可以看出每降价5元,日销量增加______件,从而可以估计降价之前的日销量为________件,当售价为500元时,日销量为________件.知1-练2 一个正方形的边长为3 cm,它的各边边长减少x cm后,得到的新正方形的周长为y cm,y与x之间的函数解析式是( )
A.y=12-4x B.y=4x-12
C.y=12-x D.以上都不对知1-练3 已知某品牌东北大米6元/kg,请你根据条件完成下表:知1-练4 (2016·黄石)向一个半径为R,容积为V的球形容器内注水,其截面如图所示,则反映容器内水的体积y与容器内水深x之间的函数关系的图象可能是( )2知识点三种函数表示法间的关系知2-讲 列表法的特点是一目了然.从表格中已有的自变量
的每一个值.不需计算就可以直接查出与它对应的函数
值.使用起来很方便,但也布局限性,因为列出的对应
值是有限的,而且在表格中.也不容易看出x与y之间对
应的规律.图象法的特点可以直观、形象地把自变量与
函数之间的关系表示出来,它的不足之处是由图象只能
得到近似的数量关系.解析式法的特点是简单明了.能
准确地反映整个变化过程中自变量与函数间的相互关系,
但求对应值时,往往要经过比较复杂的计算 .注意:列表法、图象法、解析法虽然形式不同、但都
反映了问题中的两个变量——x自变量)、y(函数)的
关系.我们在解决问题时,常常综合运用这三种表
示法来深入地研究自变量与函数的关系式的性质.
同一个函数关系可以用不同的方法表示.知2-讲知2-讲例2 某年初,我国西南部分省市遭
遇了严重干旱.某水库的蓄水
量随着时间的增加而减小,干
旱持续时间t(天)与蓄水量V(万
立方米)的变化情况如图所示,
根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t取0至60天之间的任一值时,对应几个V值?
(4)V可以看作t的函数吗?若可以,写出函数解析式.知2-讲(1)通过读图可知,横坐标表示干旱持续时间,纵坐标表
示水库蓄水量,因此它表示的是干旱持续时间与水库
蓄水量之间的关系;
(2)根据图象信息确定每个特殊点的坐标即可;
(3)观察图象可得;
(4)可根据函数的定义来判断.
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:导引:解:知2-讲(3)当t取0至60天之间的任一值时,对应着一个V值.
(4)V可以看作t的函数.
根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,由
此可得出函数解析式为
V=1 200- =-20t+1 200(0≤t≤60). 本例通过“形”,即图象中的信息,用列表及
解析式这些“数”来表示说明,三种函数表示方法
之间有互补性,是可以相互转化的,体现了数形结
合思想的应用.知2-讲1 某气象中心观测一场沙尘暴从发生到结束的全过 程,绘制了风速y(km/h)与时间t(h)之间的关系图如图所示.
(1)这个图反映了_______
与________之间的关
系.
(2)根据此图填写下面的表格:知2-练(3)当t取0 h到50 h之间的一个确定的值时,相应的风速
________确定(填“能”或“不能”).
(4)风速y可以看作时间t的函数吗?知2-练2 常用的三种函数的表示方法是:________、________、________,其中________可以由表中已有自变量的每一个值直接得出相应的函数值;________能准确地反映整个变化过程中函数与自变量之间的关系;________能直观、形象地表示函数关系.3 要形象、直观地表示某市某天的气温与时间的函数关系,适宜用( )
A.列表法 B.解析式法
C.图象法 D.以上都可以知2-练1.函数的三种表示方法.注意:解析式法应用较多,有的函数图象可以用三种
方法中的任意一种表示,而有的只能用其中的一种
或者是两种方法表示.如某地某天的天气变化与时
间的关系,很难用解析式法进行描述.
三种函数表示法间的关系2课时流程逐点
导讲练课堂小结作业提升某公司招聘
条件:初中学历以上,团员优先,能吃苦耐劳
年舲:16-25岁
待遇:按钟点计酬(工资标准为每小时8元)
假如你是初中毕业生被聘用,设工作时数为t(时),应得
工资额为m(元),则m=8t.
取一些不同的t的值,求出相应的m的值:
t= 2 时,m= 16 元;t= 3 时,m= 24 元;
…….
在根据不同的工作时数计算你应得工资额的过程中你
用了函数的哪些表示方法呢?1知识点函数的表示法知1-讲函数的表示方法有三种:(1)解析式法;(2)列表法;
(3)图象法.用来表达函数关系的数学式子叫做函数解
析式或函数关系式.用关于自变量的数学式子表示函
数与自变量的方法叫做解析式法. 用表格表示函数关
系的方法,叫做列表法. 用图象表示函数关系的方法.
叫做图象法.知1-讲例1 一个水库的水位在最近5 h内持续上涨.下表记录了这5 h内6个时间点的水位高度,其中t表示时间,y表示水位高度.(1)在平面直角坐标系中描出表中数据对应的点,这些点是
否在一条直线上?由此你能发现水位变化有什么规律吗?
(2)水位高度y是否为时间t的函数?如果是,试写出一个符
合表中数据的函数解析式,并画出这个函数的图象.这个
函数能表示水位的变化规律吗?
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高
度将为多少米.知1-讲(1)如图,描出表中数据对应的点.可以看出,这6个点
在一 条直线上.再结合表中数据,可以发现每小时水
位上升0.3m.由此猜想,如果画出这5 h内其他时刻
(如t=2. 5 h等)及其水位高度所对应的点,它们可能
也在这条直线上,即在这
个时间段中水位可能是始
终以同一速度均匀上升的.解:知1-讲(2) 由于水位在最近5 h内持续上涨,对于时间 t的每一个确定
的值,水位高度 y都有唯一的值与其对应,所以y是t的函
数.开始时水位高度为3 m,以后每小时水位上升0.3 m.函
数y=0. 3t+3(0≤t≤5)是符合表中数据的一个函数,它表
示经过t h水位上升0.3t m,即水位y为(0. 3t+3)m.其图象是
(1)图中点A(0, 3) 和点B(5, 4.5)之间的线段AB.
如果在这5 h内,水位一直匀速上升, 即升速为0.3m/h,
那么函数y=0.3t+3(0≤t≤5)就精确地表示了这种变化规律.
即使在这5 h内,水位的升速有些变化,而由于每小时水位
上升0.3 m是确定的,因此这个函数也可以近似地表示水位
的变化规律.知1-讲(3)如果水位的变化规律不变,
则可利用上述函数预测,
再过2 h,t=5+2=7(h)时,
水位高度
y=0. 3×7+3= 5.1(m).
把(1)图中的函数图象(线段
AB)向右延伸到t=7所对应的位置,得右图,从它也
能看出这时的水位高度约为5.1 m.(1)从图中获取信息首先要弄清楚横、纵轴分别表示
什么意义,再对问题进行分析.
(2)在实际问题中,有的横轴和纵轴上的单位长度可
以不一致,这对问题的结论没有影响,但每条坐
标轴上的单位长度必须要一致.知1-讲知1-练1 某商品原价为560元,随着不同幅度的降价,日销量(件)发生相应的变化,如下表:
这个表反映了________个变量之间的关系,________是自变量,______是函数.从表中可以看出每降价5元,日销量增加______件,从而可以估计降价之前的日销量为________件,当售价为500元时,日销量为________件.知1-练2 一个正方形的边长为3 cm,它的各边边长减少x cm后,得到的新正方形的周长为y cm,y与x之间的函数解析式是( )
A.y=12-4x B.y=4x-12
C.y=12-x D.以上都不对知1-练3 已知某品牌东北大米6元/kg,请你根据条件完成下表:知1-练4 (2016·黄石)向一个半径为R,容积为V的球形容器内注水,其截面如图所示,则反映容器内水的体积y与容器内水深x之间的函数关系的图象可能是( )2知识点三种函数表示法间的关系知2-讲 列表法的特点是一目了然.从表格中已有的自变量
的每一个值.不需计算就可以直接查出与它对应的函数
值.使用起来很方便,但也布局限性,因为列出的对应
值是有限的,而且在表格中.也不容易看出x与y之间对
应的规律.图象法的特点可以直观、形象地把自变量与
函数之间的关系表示出来,它的不足之处是由图象只能
得到近似的数量关系.解析式法的特点是简单明了.能
准确地反映整个变化过程中自变量与函数间的相互关系,
但求对应值时,往往要经过比较复杂的计算 .注意:列表法、图象法、解析法虽然形式不同、但都
反映了问题中的两个变量——x自变量)、y(函数)的
关系.我们在解决问题时,常常综合运用这三种表
示法来深入地研究自变量与函数的关系式的性质.
同一个函数关系可以用不同的方法表示.知2-讲知2-讲例2 某年初,我国西南部分省市遭
遇了严重干旱.某水库的蓄水
量随着时间的增加而减小,干
旱持续时间t(天)与蓄水量V(万
立方米)的变化情况如图所示,
根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t取0至60天之间的任一值时,对应几个V值?
(4)V可以看作t的函数吗?若可以,写出函数解析式.知2-讲(1)通过读图可知,横坐标表示干旱持续时间,纵坐标表
示水库蓄水量,因此它表示的是干旱持续时间与水库
蓄水量之间的关系;
(2)根据图象信息确定每个特殊点的坐标即可;
(3)观察图象可得;
(4)可根据函数的定义来判断.
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:导引:解:知2-讲(3)当t取0至60天之间的任一值时,对应着一个V值.
(4)V可以看作t的函数.
根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,由
此可得出函数解析式为
V=1 200- =-20t+1 200(0≤t≤60). 本例通过“形”,即图象中的信息,用列表及
解析式这些“数”来表示说明,三种函数表示方法
之间有互补性,是可以相互转化的,体现了数形结
合思想的应用.知2-讲1 某气象中心观测一场沙尘暴从发生到结束的全过 程,绘制了风速y(km/h)与时间t(h)之间的关系图如图所示.
(1)这个图反映了_______
与________之间的关
系.
(2)根据此图填写下面的表格:知2-练(3)当t取0 h到50 h之间的一个确定的值时,相应的风速
________确定(填“能”或“不能”).
(4)风速y可以看作时间t的函数吗?知2-练2 常用的三种函数的表示方法是:________、________、________,其中________可以由表中已有自变量的每一个值直接得出相应的函数值;________能准确地反映整个变化过程中函数与自变量之间的关系;________能直观、形象地表示函数关系.3 要形象、直观地表示某市某天的气温与时间的函数关系,适宜用( )
A.列表法 B.解析式法
C.图象法 D.以上都可以知2-练1.函数的三种表示方法.注意:解析式法应用较多,有的函数图象可以用三种
方法中的任意一种表示,而有的只能用其中的一种
或者是两种方法表示.如某地某天的天气变化与时
间的关系,很难用解析式法进行描述.
