19.2.2 正比例函数的图象和性质课件
文档属性
| 名称 | 19.2.2 正比例函数的图象和性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 415.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 00:00:00 | ||
图片预览







文档简介
课件22张PPT。第2课时 正比例函数的
图象和性质第十九章 一次函数19.2 一次函数1课堂讲解正比例函数的图像
正比例函数的性质2课时流程逐点
导讲练课堂小结作业提升 如图所示,这是一次比赛两个运动员的比赛情况示
意图,根据图象可知:这是一次多少距离的赛跑?谁先到
达终点?花了多少时间? 你能解答这个问题吗?这就是我
们今天要探究的内容.1知识点正比例函数的图象知1-导思考
经过原点与点(1,k) (k是常数,k≠0)的直线是哪个
函数的图象?画正比例函数的图象时,怎样画最简单?
为什么? 因为两点确定一条直线,所以可用两点法画正
比例函数y=kx(k≠0)的图象.一般地,过原点和点(1,k)
(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的
图象.知1-导知1-讲 由于正比例函数是一种特殊的函数,因为正比
例函数的图象是一条直线,正比例函数y=kx(k≠0)
的图象也称为直线y=kx(k≠0).由于当x=0时,
y=0,故直线y=kx是经过(0,0)点的直线,也就是
直线y=kx只经过两个象限.因此画正比例函数的
图象时,只要确定除(0,0)点以外的一个点,再经
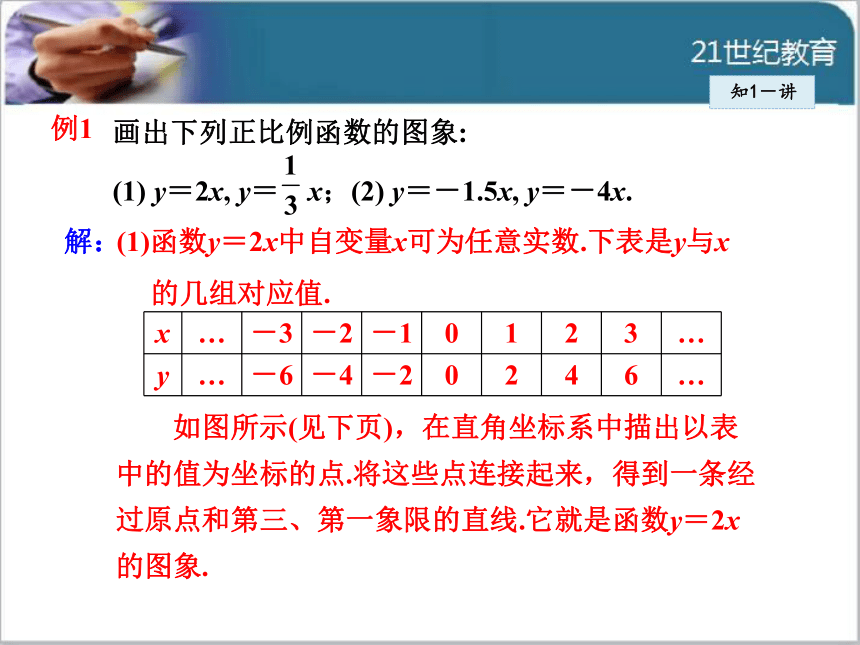
过该点与原点作直线即可.知1-讲例1 画出下列正比例函数的图象:
(1) y=2x, y= x;(2) y=-1.5x, y=-4x.(1)函数y=2x中自变量x可为任意实数.下表是y与x
的几组对应值.解: 如图所示(见下页),在直角坐标系中描出以表
中的值为坐标的点.将这些点连接起来,得到一条经
过原点和第三、第一象限的直线.它就是函数y=2x
的图象.知1-讲用同样的方法,可以得到
函数y= 的图象(如图).
它也是一条经过原点和第
三、第一象限的直线.
(2)函数y=-1.5x中自变量x
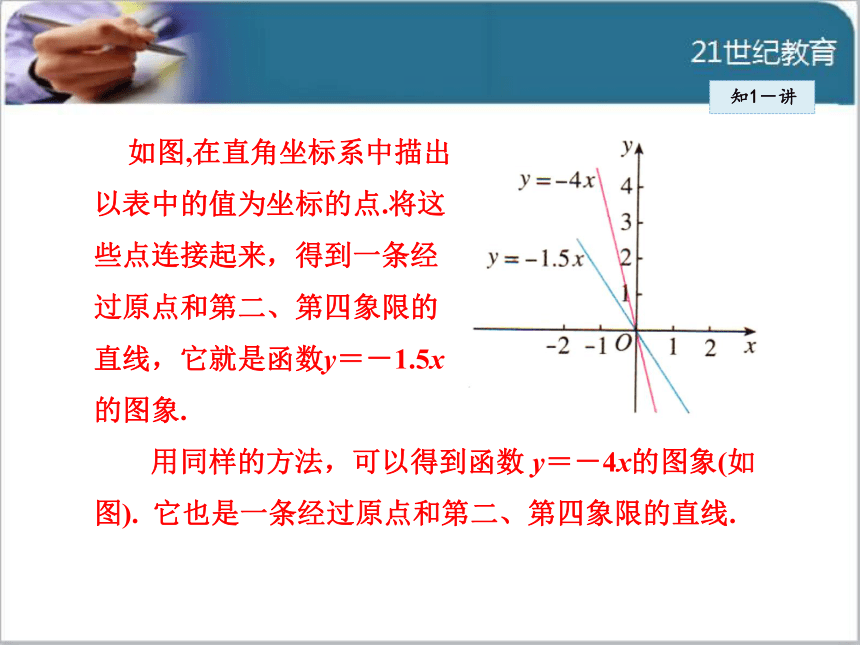
可为任意实数.下表是y与x的几组 对应值.知1-讲如图,在直角坐标系中描出
以表中的值为坐标的点.将这
些点连接起来,得到一条经
过原点和第二、第四象限的
直线,它就是函数y=-1.5x
的图象.
用同样的方法,可以得到函数 y=-4x的图象(如
图). 它也是一条经过原点和第二、第四象限的直线.知1-练1 用你认为最简单的方法画出下列函数的图象:
(1) (2) y=-3x.
2 下列各点在函数 的图象上的是( )
A. B.
C. D. 知1-练3 (2015·北海)正比例函数y=kx的图象如图所示,则k的取值范围是( )
A.k>0
B.k<0
C.k>1
D.k<12知识点正比例函数的性质知2-导 函数y=2x和y= x的图象经过第三、第一象限,
从左向右上升;函数y=-1.5x和 y=一4x.的图象经过
第二、第四象限,从左向右下降.知2-讲 一般地,正比例函数y=kx(k是常数,k≠0)的图
象是一条直线,这条直线经过原点,我们称它为直线
y=kx.
正比例函数具有以下性质:
(1)图象一定过原点(0,0);
(2)当k>0时,直线y=kx经过第一、第三象限,从左向
右上升,即随着x的增大y也增大;
(3)当k<0时,直线y=kx经过第二、第四象限,从左向
右下降,即随着x的增大y反而减小.知2-讲例2 〈珠海〉已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).方法一:把点A、点B的坐标分别代入函数
y=3x,求出y1,y2的值比较大小即可.
方法二:画出正比例函数y=3x的图象,在
函数图象上标出点A、点B,利用数形结合
思想来比较y1,y2的大小.如图,观察图形,
显然可得y1>y2.
方法三:根据正比例函数的增减性来比较函数值的大小.
根据正比例函数的性质,当k>0时,y随x的增大而增大,
即可得y1>y2.导引:> 正比例函数图象上两点的纵坐标的大小与比例
系数及自变量的大小有关;比例系数是正数时,函
数值随自变量的增大而增大;比例系数是负数时,
函数值随自变量的增大而减小.本例的解法中,方
法一是利用求值比较法;方法二是利用数形结合思
想,用“形”上的点的位置来比较“数”的大小;
方法三是利用函数的增减性来比较大小.知2-讲1 P1(x1,y1),P2(x2,y2)是正比例函数y= 的图
象上的两点,则下列判断正确的是( )
A.y1>y2
B.y1<y2
C.当x1<x2时,y1>y2
D.当x1<x2时,y1<y2,知2-练知2-练2 (2015·陕西)设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m等于( )
A.2 B.-2 C.4 D.-4
3 关于函数y=-2x,下列判断正确的是( )
A.图象经过第一、三象限
B.y随x的增大而增大
C.若(x1,y1),(x2,y2)是该函数图象上的两点,
则当x1y2
D.不论x为何值,总有y<0知2-讲例3 已知正比例函数y1=k1x,y1随x增大1个单位而增加6个
单位;y2=k2x,y2随x增大1个单位而减少2个单位,且
y=2y1+3y2.
(1)确定y与x的函数解析式,并计算当x=-2时的函数值;
(2)当函数值y是12时,求自变量的对应值.根据正比例函数的性质确定函数的解析式.
不能盲目做题,只有在搞清楚概念的基础上做才是有效的,
因为盲目、大量做题,有时候错误或者误解也会得到巩固,
纠正起来更加困难.导引:知2-讲(1)因为y1随x增大1个单位而增加6个单位,所以y1=6x.
因为y2随x增大1个单位而减少2个单位,所以y2=-2x.
因为y=2y1+3y2,所以y=2×6x+3×(-2x),即y=6x.
因此当x=-2时,函数值是-12.
(2)当函数值y是12时,自变量的对应值满足6x=12,
解得x=2.解: 已知正比例函数的函数值随着自变量增大1个
单位时,函数值的增加量是某个数值,比例系数的
值就是这个增量;反之,当函数值随着自变量增大1
个单位时,函数值的减少量是某个数值,比例系数
就是这个减少量的相反数.知2-讲1 函数y=(k2-4)x+(k+1)是正比例函数,且y随x的增大而减小.求函数的解析式.
2 已知y与x成正比例,且当x=3时,y=-9.
(1)求y与x之间的函数关系式;
(2)画出函数图象;
(3)点P(-1,3)和Q(-6,3)是否在此函数图象上?知2-练图象:正比例函数y=kx(k是常数,k≠0)的图象是
一条经过原点的直线,我们称它为直线y=kx.
性质:
当k>0时,直线y=kx经过第一、三象限,从
左向右上升,y随着x的增大而增大;
当k<0时,直线y=kx经过第二、四象限,从
左向右下降,y随着x的增大而减小.
图象和性质第十九章 一次函数19.2 一次函数1课堂讲解正比例函数的图像
正比例函数的性质2课时流程逐点
导讲练课堂小结作业提升 如图所示,这是一次比赛两个运动员的比赛情况示
意图,根据图象可知:这是一次多少距离的赛跑?谁先到
达终点?花了多少时间? 你能解答这个问题吗?这就是我
们今天要探究的内容.1知识点正比例函数的图象知1-导思考
经过原点与点(1,k) (k是常数,k≠0)的直线是哪个
函数的图象?画正比例函数的图象时,怎样画最简单?
为什么? 因为两点确定一条直线,所以可用两点法画正
比例函数y=kx(k≠0)的图象.一般地,过原点和点(1,k)
(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的
图象.知1-导知1-讲 由于正比例函数是一种特殊的函数,因为正比
例函数的图象是一条直线,正比例函数y=kx(k≠0)
的图象也称为直线y=kx(k≠0).由于当x=0时,
y=0,故直线y=kx是经过(0,0)点的直线,也就是
直线y=kx只经过两个象限.因此画正比例函数的
图象时,只要确定除(0,0)点以外的一个点,再经
过该点与原点作直线即可.知1-讲例1 画出下列正比例函数的图象:
(1) y=2x, y= x;(2) y=-1.5x, y=-4x.(1)函数y=2x中自变量x可为任意实数.下表是y与x
的几组对应值.解: 如图所示(见下页),在直角坐标系中描出以表
中的值为坐标的点.将这些点连接起来,得到一条经
过原点和第三、第一象限的直线.它就是函数y=2x
的图象.知1-讲用同样的方法,可以得到
函数y= 的图象(如图).
它也是一条经过原点和第
三、第一象限的直线.
(2)函数y=-1.5x中自变量x
可为任意实数.下表是y与x的几组 对应值.知1-讲如图,在直角坐标系中描出
以表中的值为坐标的点.将这
些点连接起来,得到一条经
过原点和第二、第四象限的
直线,它就是函数y=-1.5x
的图象.
用同样的方法,可以得到函数 y=-4x的图象(如
图). 它也是一条经过原点和第二、第四象限的直线.知1-练1 用你认为最简单的方法画出下列函数的图象:
(1) (2) y=-3x.
2 下列各点在函数 的图象上的是( )
A. B.
C. D. 知1-练3 (2015·北海)正比例函数y=kx的图象如图所示,则k的取值范围是( )
A.k>0
B.k<0
C.k>1
D.k<12知识点正比例函数的性质知2-导 函数y=2x和y= x的图象经过第三、第一象限,
从左向右上升;函数y=-1.5x和 y=一4x.的图象经过
第二、第四象限,从左向右下降.知2-讲 一般地,正比例函数y=kx(k是常数,k≠0)的图
象是一条直线,这条直线经过原点,我们称它为直线
y=kx.
正比例函数具有以下性质:
(1)图象一定过原点(0,0);
(2)当k>0时,直线y=kx经过第一、第三象限,从左向
右上升,即随着x的增大y也增大;
(3)当k<0时,直线y=kx经过第二、第四象限,从左向
右下降,即随着x的增大y反而减小.知2-讲例2 〈珠海〉已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).方法一:把点A、点B的坐标分别代入函数
y=3x,求出y1,y2的值比较大小即可.
方法二:画出正比例函数y=3x的图象,在
函数图象上标出点A、点B,利用数形结合
思想来比较y1,y2的大小.如图,观察图形,
显然可得y1>y2.
方法三:根据正比例函数的增减性来比较函数值的大小.
根据正比例函数的性质,当k>0时,y随x的增大而增大,
即可得y1>y2.导引:> 正比例函数图象上两点的纵坐标的大小与比例
系数及自变量的大小有关;比例系数是正数时,函
数值随自变量的增大而增大;比例系数是负数时,
函数值随自变量的增大而减小.本例的解法中,方
法一是利用求值比较法;方法二是利用数形结合思
想,用“形”上的点的位置来比较“数”的大小;
方法三是利用函数的增减性来比较大小.知2-讲1 P1(x1,y1),P2(x2,y2)是正比例函数y= 的图
象上的两点,则下列判断正确的是( )
A.y1>y2
B.y1<y2
C.当x1<x2时,y1>y2
D.当x1<x2时,y1<y2,知2-练知2-练2 (2015·陕西)设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m等于( )
A.2 B.-2 C.4 D.-4
3 关于函数y=-2x,下列判断正确的是( )
A.图象经过第一、三象限
B.y随x的增大而增大
C.若(x1,y1),(x2,y2)是该函数图象上的两点,
则当x1
D.不论x为何值,总有y<0知2-讲例3 已知正比例函数y1=k1x,y1随x增大1个单位而增加6个
单位;y2=k2x,y2随x增大1个单位而减少2个单位,且
y=2y1+3y2.
(1)确定y与x的函数解析式,并计算当x=-2时的函数值;
(2)当函数值y是12时,求自变量的对应值.根据正比例函数的性质确定函数的解析式.
不能盲目做题,只有在搞清楚概念的基础上做才是有效的,
因为盲目、大量做题,有时候错误或者误解也会得到巩固,
纠正起来更加困难.导引:知2-讲(1)因为y1随x增大1个单位而增加6个单位,所以y1=6x.
因为y2随x增大1个单位而减少2个单位,所以y2=-2x.
因为y=2y1+3y2,所以y=2×6x+3×(-2x),即y=6x.
因此当x=-2时,函数值是-12.
(2)当函数值y是12时,自变量的对应值满足6x=12,
解得x=2.解: 已知正比例函数的函数值随着自变量增大1个
单位时,函数值的增加量是某个数值,比例系数的
值就是这个增量;反之,当函数值随着自变量增大1
个单位时,函数值的减少量是某个数值,比例系数
就是这个减少量的相反数.知2-讲1 函数y=(k2-4)x+(k+1)是正比例函数,且y随x的增大而减小.求函数的解析式.
2 已知y与x成正比例,且当x=3时,y=-9.
(1)求y与x之间的函数关系式;
(2)画出函数图象;
(3)点P(-1,3)和Q(-6,3)是否在此函数图象上?知2-练图象:正比例函数y=kx(k是常数,k≠0)的图象是
一条经过原点的直线,我们称它为直线y=kx.
性质:
当k>0时,直线y=kx经过第一、三象限,从
左向右上升,y随着x的增大而增大;
当k<0时,直线y=kx经过第二、四象限,从
左向右下降,y随着x的增大而减小.
