19.2.4 一次函数的图象与性质课件
文档属性
| 名称 | 19.2.4 一次函数的图象与性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 765.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 00:00:00 | ||
图片预览









文档简介
课件32张PPT。第4课时 一次函数的
图象与性质第十九章 一次函数19.2 一次函数1课堂讲解一次函数y=kx+b的图象
直线y=kx+b的位置与系数k,b的关系
一次函数y=kx+b的性质2课时流程逐点
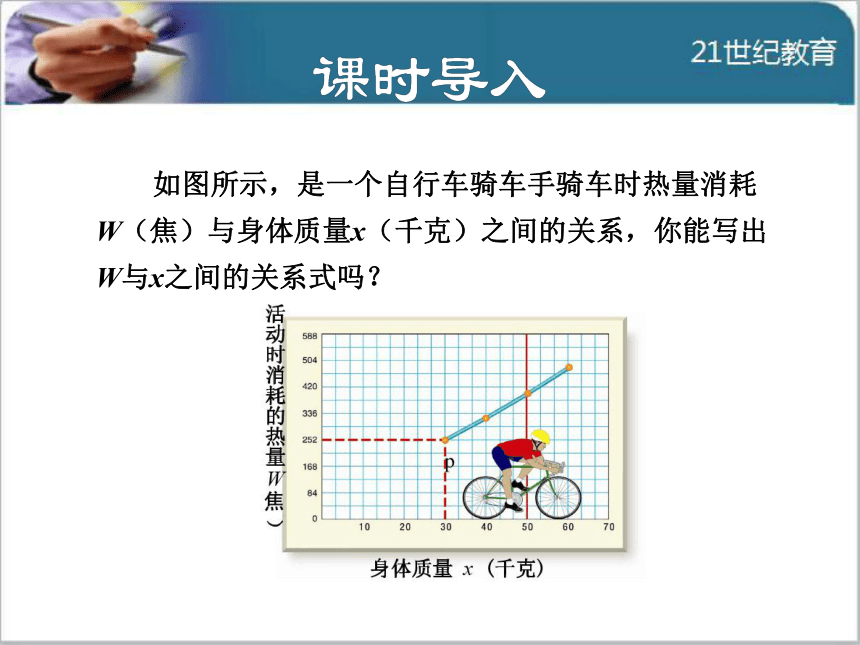
导讲练课堂小结作业提升 如图所示,是一个自行车骑车手骑车时热量消耗
W(焦)与身体质量x(千克)之间的关系,你能写出
W与x之间的关系式吗?1知识点一次函数y=kx+b的图象知1-讲 一次函数的图象是一条直线,这条直线与坐标轴
有交点,正比例函数只有一个交点,一般的一次函数
有两个交点.
注意:一次函数图象的画法与我们前边学过的函数图
象的画法一样,其步骤为列表、描点、连线.通过实际
操作,我们可得出:知1-讲(1)一次函数 y=kx+b(k,b是常数,k≠0)的图象是一
条直线.由两点确定一条直线可知,在画一次函数图
象时,只要描出函数图象中的两个点就可画出此函
数的图象.
(2)一般地,一次函数y=kx+b(k,b是常数,k≠0)
都过(0,b) (与y轴交点坐标)和( )(与x轴交点
坐标)两点. 一次函数的图象是一条直线,我们称它为直线
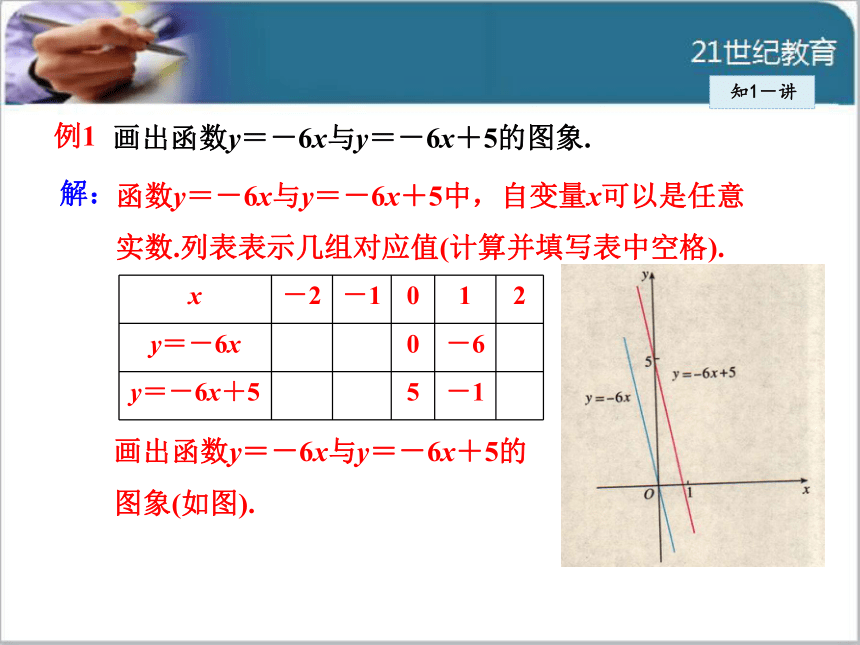
y=kx+b;它必过(0,b)和( )两点.知1-讲知1-讲例1 画出函数y=-6x与y=-6x+5的图象.函数y=-6x与y=-6x+5中,自变量x可以是任意
实数.列表表示几组对应值(计算并填写表中空格).解:画出函数y=-6x与y=-6x+5的
图象(如图). 画一次函数y=kx+b(k≠0)的图象,通常选取该
直线与y轴的交点(横坐标为0的点)和直线与x轴的交
点(纵坐标为0的点),由两点确定一条直线得一次函
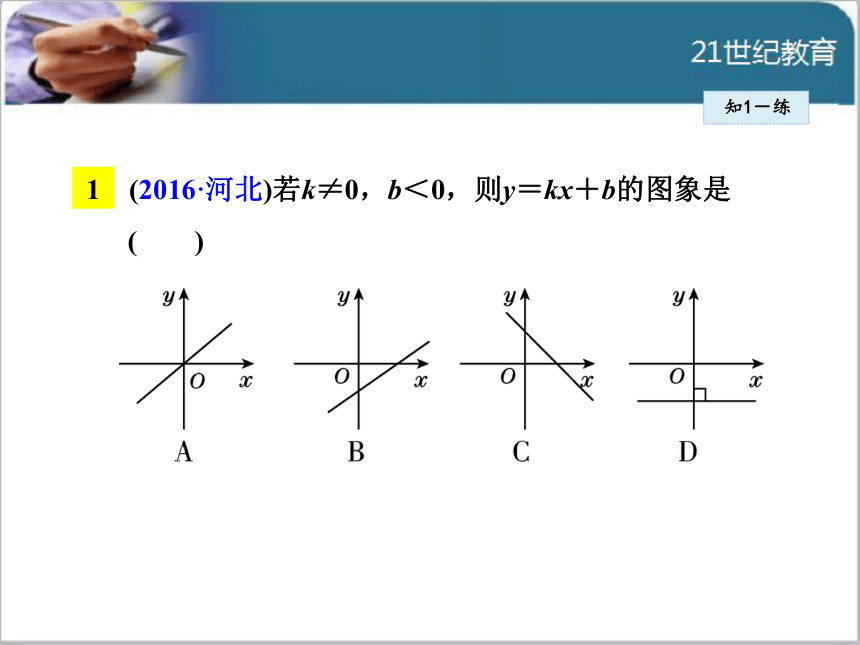
数的图象.知1-讲1 (2016·河北)若k≠0,b<0,则y=kx+b的图象是
( )知1-练知1-练2 (2016·雅安)若式子 +(k-1)0有意义,则一次
函数y=(1-k)x+k-1的图象可能是( )2知识点直线y=kx+b的位置与系数k,b的关系知2-导思考
比较上面两个函数的图象的相同点与不同点,填
出你的观察结果:
这两个函数的图象形状都是______,并且倾斜程
度______.函数y=-6x的图象经过原点,函数y=-6x
+5的图象与y轴交于点_______,即它可以看作由直线
y=-6x向____平移____个单位长度而得到.知2-导 比较两个函数解析式,你能说出两个函数的图
象有上述关系的道理吗?
联系上面结果,考虑一次函数y=kx+b(k≠0)的
图象是什么形状,它与直线y=kx(k≠0)有什么关系. 比较一次函数y=kx+b(k≠0)与正比例函数y=
kx(k≠0)的解析式,容易得出:
一次函数y=kx+b(k≠0)的图象可以由直线
y=kx平移|b|个单位长度得到(当b>时,向上平移;
当b<0时,向下平移).一次函数y=kx+b(k≠0)的图
象也是一条直线,我们称它为直线y=kx+b.知2-导知2-讲从 k、b的值看一次函数的图像
(1)当k>0,b>0时,图象过一、二、三象限;
(2)当k>0,b<0时,图象过一、三、四象限;
(3)当k<0,b>0时,图象过一、二、四象限;
(4)当k<0,b<0时,图象过二、三、四象限. 知2-讲例2 已知直线y=(1-3k)x+2k-1.
(1)k为何值时,直线与y轴交点的纵坐标是-2?
(2)k为何值时,直线经过第二、三、四象限?
(3)k为何值时,已知直线与直线 y=-3x-5平行?(1)可令2k-1=-2或将(0,-2)代入函数解析式即可求
得k值;
(2)直线经过第二、三、四象限,说明y=kx+b中的k<0,
b<0,即 解不等式组求出k的取值范围即可;
(3)两直线若平行,则它们的自变量的系数应相等,
所以1-3k=-3且2k-1≠-5,可求出k值.导引:知2-讲(1)当x=0时,y=-2,即当2k-1=-2,k= 时,
直线与y轴交点的纵坐标是-2.
(2)当 直线经过第二、三、四
象限.
(3)当1-3k=-3,即当 时,2k-1= ≠-5,
此时,已知直线与直线 y=-3x-5平行.解: 直线经过第二、三、四象限与不经过第一象限
的区别是:经过第二、三、四象限时函数解析式中b
不能等于0;不经过第一象限时函数解析式中的b可
能等于0.知2-讲1 〈攀枝花〉当kb<0时,一次函数y=kx+b的图象一定经过( )
A.第一、三象限 B.第一、四象限
C.第二、三象限 D.第二、四象限
2 若一次函数y=kx+b的图象经过第一、三、四象 限,则k,b的取值范围是( )
A.k>0,b>0 B.k<0,b>0
C.k<0,b<0 D.k>0,b<0知2-练知2-练3 (2015·遂宁)直线y=2x-4与y轴的交点坐标是( )
A.(4,0) B.(0,4)
C.(-4,0) D.(0,-4)3知识点一次函数y=kx+b的性质知3-讲例3 画出函数y=2x-1与y=-0.5x+1的图象.由于一次函数的图象是直线,因此只要确定两个点就
能画出它.分析:列表表示当x=0,x=1时两个函数的对应值(见下表).解: 过点(0, -1)与点(1,1)画出直线y=2x-1;过点
(0, 1)与点(1,0.5) 画出直线y=-0.5x+1.(如图)知3-讲探究
画出函数y=x+l,y=-x+l,y=2x+1,
y=-2x +1的图象.由它们联想:一次函数解析式
y=kx+b(k,b是常数,k≠0)中,k的正负对函数图
象有什么影响?知3-导观察前面一次函数的图象,可以发现规律:
当k>0时,直线y=kx+b从左向右上升;
当k<0时,直线y=kx+b从左向右下降.
由此可 知,一次函数y=kx+b(k,b是常数,k≠0)
具有如下性质:
当k>0时,y随x的增大而増大;
当k<0时,y随x的增大而减小.知3-导知3-讲要点精析:
(1)在实际问题中,当自变量x的取值受限制时,一次函数
y=kx+b的图象就不一定是一条直线了,有时是线段、
射线或直线上的部分点.
(2)k决定直线的倾斜角度:
k>0?直线y=kx+b在x轴上方的部分与x轴正方向的夹
角为锐角;
k<0?直线y=kx+b在x轴上方的部分与x轴正方向的夹
角为钝角;
k1=k2?直线y1=k1x+b1∥直线y2=k2x+b2(b1≠b2).
(3)k>0?y随x的增大而增大;k<0?y随x的增大而减小.知3-讲例4 已知一次函数y=(6+3m)x+(m-4),y随x的增大而增大,函数的图象与y轴的交点在y轴的负半轴上,求m的取值范围.根据一次函数的性质可知,6+3m>0,且m-4<0,
解不等式组即可.导引:根据题意,得 解得-2<m<4.
所以m的取值范围是-2<m<4.解:对于一次函数y=kx+b
(1)判断k值符号的方法:
①增减性法:当y随x增大而增大时,k>0;
反之,k<0.
②直线升、降法:当直线从左到右上升时,k>0;
反之,k<0.
③经过象限法:当直线过第一、三象限时,k>0;
当直线过第二、四象限时,k<0.知3-讲(2)判断b值的方法:
与y轴交点法,即若直线y=kx+b与y轴交于正半
轴,则b>0;
与y轴交于负半轴,则b<0;
与y轴交于原点,则b=0.知3-讲1 〈济南〉若一次函数y=(m-3)x+5的函数值y随x的增大而增大,则( )
A.m>0 B.m<0 C.m>3 D.m<3
2 (2015·海南)点(-1,y1),(2,y2)是直线y=2x+1上的两点,则y1______y2(填“>”“=”或“<”).知3-练知3-练3 下列函数中,同时满足下面两个条件的是( )
①y随着x的增大而增大;
②其图象与x轴的正半轴相交.
A.y=-2x-1 B.y=-2x+1
C.y=2x-1 D.y=2x+1 一次函数 y=kx+b(k、b是常数,k≠0)的图像和性
质与k、b的值紧密相连,归纳起来主要有以下几方面.
1.从k的值来看性质:
(1)从k的值的正负看一次函数的性质
当k>0时,y随x的增大而增大.
当k<0时,y随x的增大而减小.
(2)从k的值相等看一次函数的性质
当几个一次函数中k的值相同时,这几个函数的图像
是一组互相平行的直线.(3)从k的绝对值看一次函数的性质
几个函数中,当|k|较大时,直线看起来比较“陡”,
即直线的倾斜度大.
|k|较小时,直线看起来比较“缓”,即直线的倾斜度小.
当k>0时,k越大,直线与x轴正半轴所成的角度越大;
当k<0时, |k|越大,直线与x轴负半轴所成的角越大.
2.从b的值看一次函数的图像
(1)当b>0时,图像交y轴正半轴;
(2)当b<0时,图像交y轴负半轴.3.从 k、b的值看一次函数的图像
(1)当k>0,b>0时,图象过一、二、三象限;
(2)当k>0,b<0时,图象过一、三、四象限;
(3)当k<0,b>0时,图象过一、二、四象限;
(4)当k<0,b<0时,图象过二、三、四象限.
图象与性质第十九章 一次函数19.2 一次函数1课堂讲解一次函数y=kx+b的图象
直线y=kx+b的位置与系数k,b的关系
一次函数y=kx+b的性质2课时流程逐点
导讲练课堂小结作业提升 如图所示,是一个自行车骑车手骑车时热量消耗
W(焦)与身体质量x(千克)之间的关系,你能写出
W与x之间的关系式吗?1知识点一次函数y=kx+b的图象知1-讲 一次函数的图象是一条直线,这条直线与坐标轴
有交点,正比例函数只有一个交点,一般的一次函数
有两个交点.
注意:一次函数图象的画法与我们前边学过的函数图
象的画法一样,其步骤为列表、描点、连线.通过实际
操作,我们可得出:知1-讲(1)一次函数 y=kx+b(k,b是常数,k≠0)的图象是一
条直线.由两点确定一条直线可知,在画一次函数图
象时,只要描出函数图象中的两个点就可画出此函
数的图象.
(2)一般地,一次函数y=kx+b(k,b是常数,k≠0)
都过(0,b) (与y轴交点坐标)和( )(与x轴交点
坐标)两点. 一次函数的图象是一条直线,我们称它为直线
y=kx+b;它必过(0,b)和( )两点.知1-讲知1-讲例1 画出函数y=-6x与y=-6x+5的图象.函数y=-6x与y=-6x+5中,自变量x可以是任意
实数.列表表示几组对应值(计算并填写表中空格).解:画出函数y=-6x与y=-6x+5的
图象(如图). 画一次函数y=kx+b(k≠0)的图象,通常选取该
直线与y轴的交点(横坐标为0的点)和直线与x轴的交
点(纵坐标为0的点),由两点确定一条直线得一次函
数的图象.知1-讲1 (2016·河北)若k≠0,b<0,则y=kx+b的图象是
( )知1-练知1-练2 (2016·雅安)若式子 +(k-1)0有意义,则一次
函数y=(1-k)x+k-1的图象可能是( )2知识点直线y=kx+b的位置与系数k,b的关系知2-导思考
比较上面两个函数的图象的相同点与不同点,填
出你的观察结果:
这两个函数的图象形状都是______,并且倾斜程
度______.函数y=-6x的图象经过原点,函数y=-6x
+5的图象与y轴交于点_______,即它可以看作由直线
y=-6x向____平移____个单位长度而得到.知2-导 比较两个函数解析式,你能说出两个函数的图
象有上述关系的道理吗?
联系上面结果,考虑一次函数y=kx+b(k≠0)的
图象是什么形状,它与直线y=kx(k≠0)有什么关系. 比较一次函数y=kx+b(k≠0)与正比例函数y=
kx(k≠0)的解析式,容易得出:
一次函数y=kx+b(k≠0)的图象可以由直线
y=kx平移|b|个单位长度得到(当b>时,向上平移;
当b<0时,向下平移).一次函数y=kx+b(k≠0)的图
象也是一条直线,我们称它为直线y=kx+b.知2-导知2-讲从 k、b的值看一次函数的图像
(1)当k>0,b>0时,图象过一、二、三象限;
(2)当k>0,b<0时,图象过一、三、四象限;
(3)当k<0,b>0时,图象过一、二、四象限;
(4)当k<0,b<0时,图象过二、三、四象限. 知2-讲例2 已知直线y=(1-3k)x+2k-1.
(1)k为何值时,直线与y轴交点的纵坐标是-2?
(2)k为何值时,直线经过第二、三、四象限?
(3)k为何值时,已知直线与直线 y=-3x-5平行?(1)可令2k-1=-2或将(0,-2)代入函数解析式即可求
得k值;
(2)直线经过第二、三、四象限,说明y=kx+b中的k<0,
b<0,即 解不等式组求出k的取值范围即可;
(3)两直线若平行,则它们的自变量的系数应相等,
所以1-3k=-3且2k-1≠-5,可求出k值.导引:知2-讲(1)当x=0时,y=-2,即当2k-1=-2,k= 时,
直线与y轴交点的纵坐标是-2.
(2)当 直线经过第二、三、四
象限.
(3)当1-3k=-3,即当 时,2k-1= ≠-5,
此时,已知直线与直线 y=-3x-5平行.解: 直线经过第二、三、四象限与不经过第一象限
的区别是:经过第二、三、四象限时函数解析式中b
不能等于0;不经过第一象限时函数解析式中的b可
能等于0.知2-讲1 〈攀枝花〉当kb<0时,一次函数y=kx+b的图象一定经过( )
A.第一、三象限 B.第一、四象限
C.第二、三象限 D.第二、四象限
2 若一次函数y=kx+b的图象经过第一、三、四象 限,则k,b的取值范围是( )
A.k>0,b>0 B.k<0,b>0
C.k<0,b<0 D.k>0,b<0知2-练知2-练3 (2015·遂宁)直线y=2x-4与y轴的交点坐标是( )
A.(4,0) B.(0,4)
C.(-4,0) D.(0,-4)3知识点一次函数y=kx+b的性质知3-讲例3 画出函数y=2x-1与y=-0.5x+1的图象.由于一次函数的图象是直线,因此只要确定两个点就
能画出它.分析:列表表示当x=0,x=1时两个函数的对应值(见下表).解: 过点(0, -1)与点(1,1)画出直线y=2x-1;过点
(0, 1)与点(1,0.5) 画出直线y=-0.5x+1.(如图)知3-讲探究
画出函数y=x+l,y=-x+l,y=2x+1,
y=-2x +1的图象.由它们联想:一次函数解析式
y=kx+b(k,b是常数,k≠0)中,k的正负对函数图
象有什么影响?知3-导观察前面一次函数的图象,可以发现规律:
当k>0时,直线y=kx+b从左向右上升;
当k<0时,直线y=kx+b从左向右下降.
由此可 知,一次函数y=kx+b(k,b是常数,k≠0)
具有如下性质:
当k>0时,y随x的增大而増大;
当k<0时,y随x的增大而减小.知3-导知3-讲要点精析:
(1)在实际问题中,当自变量x的取值受限制时,一次函数
y=kx+b的图象就不一定是一条直线了,有时是线段、
射线或直线上的部分点.
(2)k决定直线的倾斜角度:
k>0?直线y=kx+b在x轴上方的部分与x轴正方向的夹
角为锐角;
k<0?直线y=kx+b在x轴上方的部分与x轴正方向的夹
角为钝角;
k1=k2?直线y1=k1x+b1∥直线y2=k2x+b2(b1≠b2).
(3)k>0?y随x的增大而增大;k<0?y随x的增大而减小.知3-讲例4 已知一次函数y=(6+3m)x+(m-4),y随x的增大而增大,函数的图象与y轴的交点在y轴的负半轴上,求m的取值范围.根据一次函数的性质可知,6+3m>0,且m-4<0,
解不等式组即可.导引:根据题意,得 解得-2<m<4.
所以m的取值范围是-2<m<4.解:对于一次函数y=kx+b
(1)判断k值符号的方法:
①增减性法:当y随x增大而增大时,k>0;
反之,k<0.
②直线升、降法:当直线从左到右上升时,k>0;
反之,k<0.
③经过象限法:当直线过第一、三象限时,k>0;
当直线过第二、四象限时,k<0.知3-讲(2)判断b值的方法:
与y轴交点法,即若直线y=kx+b与y轴交于正半
轴,则b>0;
与y轴交于负半轴,则b<0;
与y轴交于原点,则b=0.知3-讲1 〈济南〉若一次函数y=(m-3)x+5的函数值y随x的增大而增大,则( )
A.m>0 B.m<0 C.m>3 D.m<3
2 (2015·海南)点(-1,y1),(2,y2)是直线y=2x+1上的两点,则y1______y2(填“>”“=”或“<”).知3-练知3-练3 下列函数中,同时满足下面两个条件的是( )
①y随着x的增大而增大;
②其图象与x轴的正半轴相交.
A.y=-2x-1 B.y=-2x+1
C.y=2x-1 D.y=2x+1 一次函数 y=kx+b(k、b是常数,k≠0)的图像和性
质与k、b的值紧密相连,归纳起来主要有以下几方面.
1.从k的值来看性质:
(1)从k的值的正负看一次函数的性质
当k>0时,y随x的增大而增大.
当k<0时,y随x的增大而减小.
(2)从k的值相等看一次函数的性质
当几个一次函数中k的值相同时,这几个函数的图像
是一组互相平行的直线.(3)从k的绝对值看一次函数的性质
几个函数中,当|k|较大时,直线看起来比较“陡”,
即直线的倾斜度大.
|k|较小时,直线看起来比较“缓”,即直线的倾斜度小.
当k>0时,k越大,直线与x轴正半轴所成的角度越大;
当k<0时, |k|越大,直线与x轴负半轴所成的角越大.
2.从b的值看一次函数的图像
(1)当b>0时,图像交y轴正半轴;
(2)当b<0时,图像交y轴负半轴.3.从 k、b的值看一次函数的图像
(1)当k>0,b>0时,图象过一、二、三象限;
(2)当k>0,b<0时,图象过一、三、四象限;
(3)当k<0,b>0时,图象过一、二、四象限;
(4)当k<0,b<0时,图象过二、三、四象限.
