19.2.6 一次函数的实际应用课件
图片预览






文档简介
课件22张PPT。第6课时 一次函数的
实际应用第十九章 一次函数19.2 一次函数1课堂讲解建立一次函数模型解实际问题
用一次函数解含图象的实际问题2课时流程逐点
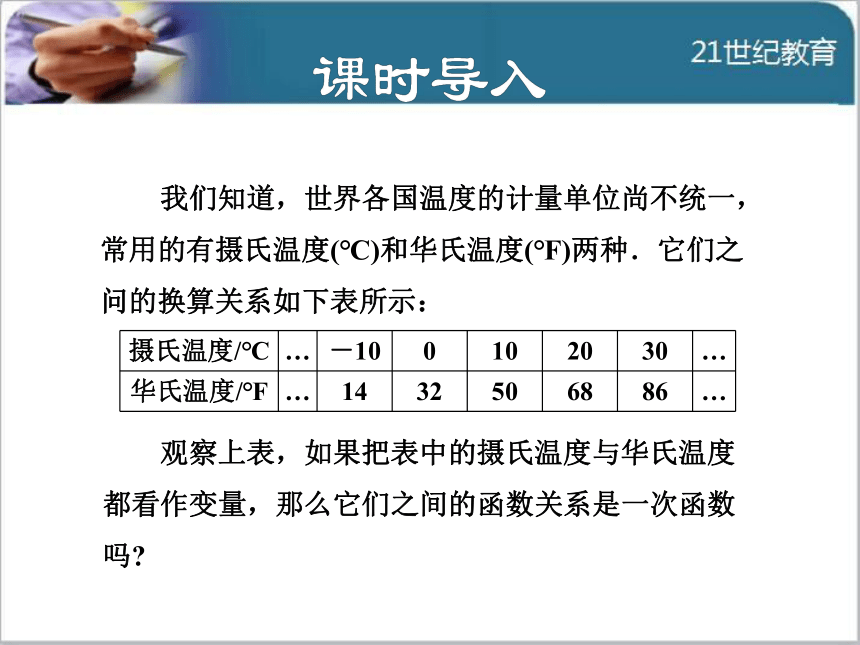
导讲练课堂小结作业提升 我们知道,世界各国温度的计量单位尚不统一,
常用的有摄氏温度(℃)和华氏温度(℉)两种.它们之
问的换算关系如下表所示: 观察上表,如果把表中的摄氏温度与华氏温度
都看作变量,那么它们之间的函数关系是一次函数
吗? 1知识点建立一次函数模型解实际问题知1-讲 在日常生活和生产实践中有不少问题的数量关系
可以用一次函数来刻画.在运用一次函数解决实际问题
时,首先判定问题中的两个变量之间是不是一次函数
关系.当确定是一次函数关系时,可求出解析式,并运
用一次函数的图象和性质进一步求得我们所需要的结
果.知1-讲 确定两个变量是否构成一次函数关系的一种常
用方法就是利用图象去获得经验公式,这种方法的
基本步骤是:
(1)通过实验、测量获得数量足够多的两个变量的对
应值;
(2)建立合适的直角坐标系,在坐标系内以各对应值
为坐标描点,并用描点法画出函数图象;
(3)观察图象特征,判定函数的类型.这样获得的函数
解析式有时是近似的. “建模”可以把实际问题转化为关于一次函数
的数学问题,它的关键是确定函数与自变量之间的
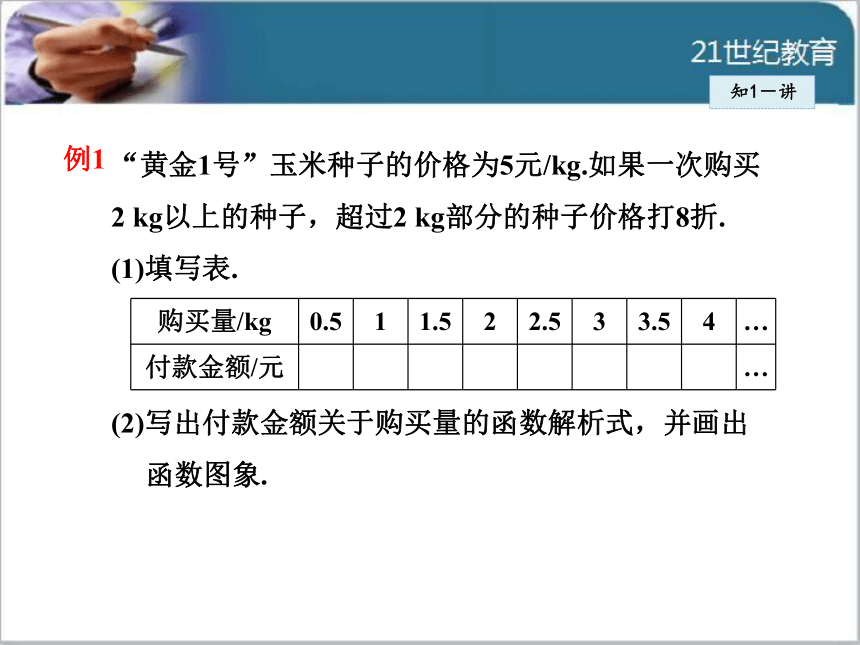
解析式,并确定实际问题中自变量的取值范围.知1-讲知1-讲例1 “黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子价格打8折.
(1)填写表.
(2)写出付款金额关于购买量的函数解析式,并画出
函数图象.知1-讲付款金额与种子价格相关. 问题中种子价格不是固
定不变的,它与购买量有关. 设购买x kg种子,当
0≤x≤2时,种子价格为5元/kg;当x>2时,其中有
2kg种子按5元/kg计价,其余的(x-2)kg(即超出2 kg
部分) 种子按4元/kg (即8折)计价,因此,写函数解析
式与画函数图象时,应对 0≤x≤2和x>2分段讨论.?分析:知1-讲(1)
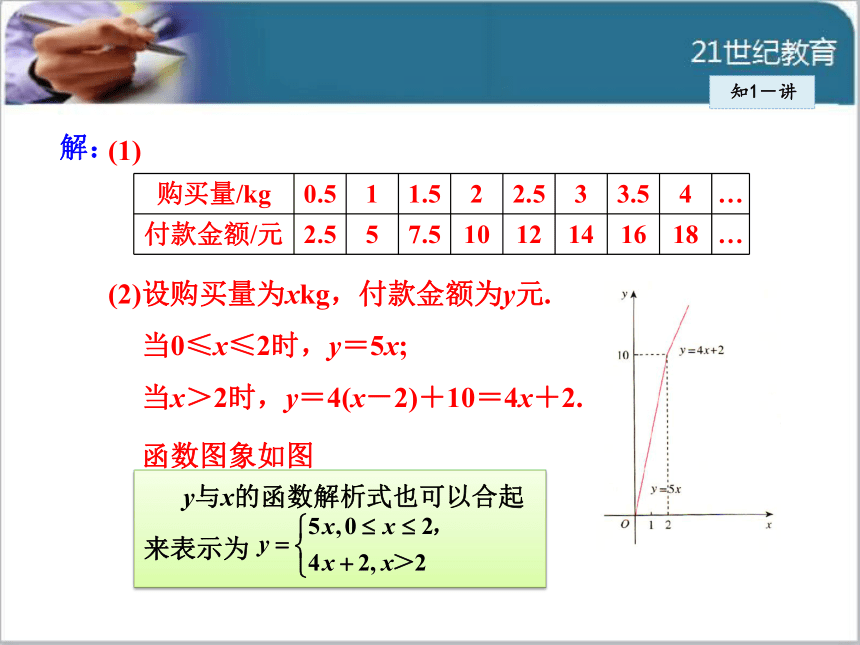
解:(2)设购买量为xkg,付款金额为y元.
当0≤x≤2时,y=5x;
当x>2时,y=4(x-2)+10=4x+2.
函数图象如图 表格信息题是中考的热点题,解决表格问题的
关键是从表格中获取正确、易于解决问题的信息;
其建模的过程是:先设出函数的解析式,然后找出
两对对应值,列出二元一次方程组,求解即可得到
解析式.知1-讲1 —个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t (单位:h)的函数解析式,并画出函数图象.知1-练2 (2015·北京)一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550(元),若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A.购买A类会员年卡 B.购买B类会员年卡
C.购买C类会员年卡 D.不购买会员年卡知1-练2知识点用一次函数解含图象的实际问题知2-导思考
你能由上面的函数解析式解决以下问题吗?由函
数图象也能解决这些问题吗?
(1)一次购买1.5 kg种子,需付款多少元?
(2) 一次购买3 kg种子,需付款多少元? 利用函数方法解决实际问题,关键是分析题中的数
量关系,联系实际生活及以前学过的内容,将实际问题
抽象、升华为一次函数模型,即建模,再利用函数的性
质解决问题.一次函数的应用主要有两种类型:
(1)给出了一次函数解析式,直接应用一次函数的性质解
决问题;
(2)只用语言叙述或用表格、图象提供一次函数的情境时,
应先求出解析式,进而利用函数性质解决问题.知2-导知2-讲例2 某移动公司采用分段计费的方法
来计算话费,月通话时间x(min)
与相应话费y(元)之间的函数图象
如图.
(1)分别求出当0≤x<100和x≥100
时,y与x之间的函数解析式.
(2)月通话为280 min时,应交话费多少元?导引:本题是一道和话费有关的分段函数问题,通过图象可以
观察到,当0≤x<100时,y与x之间是正比例函数关系;
当x≥100时,y与x之间是一次函数关系,分别用待定系
数法可求得它们的解析式.知2-讲(1)当0≤x<100时,设y1=k1x(k1≠0),
将(100,40)代入得100k1=40,解得k1=
所以正比例函数的解析式为
当x≥100时,设y2=k2x+b(k2≠0),
将(100,40)及(200,60)分别代入得
所以一次函数解析式为 解:知2-讲因为280>100,
所以将x=280代入 中,得
即月通话时间为280 min时,应交话费76元.解:(2)月通话为280 min时,应交话费多少元? 分段函数中,自变量在不同的取值范围内的解
析式不同,在解决问题时,要特别注意自变量的取
值范围的变化.分段函数的应用面广,在水费、电
费、商品促销等领域都有广泛应用.本题考查一次
函数及识图能力,体现了数形结合思想.解决问题
的关键是由图象挖掘出有用的信息,利用待定系数
法先求出函数解析式,再解决问题.知2-讲1 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如图所示.这些农作物在第10天、第30天的需水量分别为2 000千克、3 000千克,在第40天后每天的需水量比前一天增加100千克.
(1)分别求出x≤40和x>40时y与x
之间的函数关系式;
(2)如果这些农作物每天的需水量
大于或等于4 000千克时需要进
行人工灌溉,那么应从第几天
开始进行人工灌溉?知2-练知2-练2 (2016·哈尔滨)明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每时完成的绿化面积是( )
A.300 m2
B.150 m2
C.330 m2
D.450 m21.运用一次函数解决实际问题的方法:
在日常生活和生产实践中有不少问题的数量关系可以
用一次函数来刻画.在运用一次函数解决实际问题时,
首先判断问题中的两个变量之间是不是一次函数关系,
当确定是一次函数关系时,求出函数解析式,并运用
一次函数的图象和性质进一步求得所需的结果.
说明:在应用一次函数的过程中,要注意结合实际,
确定自变量的取值范围,也要结合实际情况舍去不符
合题意的解.2.用一次函数解实际问题要明确“三点”
(1)一次函数关系的建立:一种是利用问题中变量间的相
等关系去列;另一种是在已知两个变量是一次函数关
系的情况下,用待定系数法去求.
(2)利用一次函数的值随自变量值的变化情况,在自变量
的取值范围内,求最大值或最小值.利用函数图象比
较大小.
(3)正确理解题意,读懂问题至关重要.我们可以通过画
图、联想实际情况等来帮助理解题意.
实际应用第十九章 一次函数19.2 一次函数1课堂讲解建立一次函数模型解实际问题
用一次函数解含图象的实际问题2课时流程逐点
导讲练课堂小结作业提升 我们知道,世界各国温度的计量单位尚不统一,
常用的有摄氏温度(℃)和华氏温度(℉)两种.它们之
问的换算关系如下表所示: 观察上表,如果把表中的摄氏温度与华氏温度
都看作变量,那么它们之间的函数关系是一次函数
吗? 1知识点建立一次函数模型解实际问题知1-讲 在日常生活和生产实践中有不少问题的数量关系
可以用一次函数来刻画.在运用一次函数解决实际问题
时,首先判定问题中的两个变量之间是不是一次函数
关系.当确定是一次函数关系时,可求出解析式,并运
用一次函数的图象和性质进一步求得我们所需要的结
果.知1-讲 确定两个变量是否构成一次函数关系的一种常
用方法就是利用图象去获得经验公式,这种方法的
基本步骤是:
(1)通过实验、测量获得数量足够多的两个变量的对
应值;
(2)建立合适的直角坐标系,在坐标系内以各对应值
为坐标描点,并用描点法画出函数图象;
(3)观察图象特征,判定函数的类型.这样获得的函数
解析式有时是近似的. “建模”可以把实际问题转化为关于一次函数
的数学问题,它的关键是确定函数与自变量之间的
解析式,并确定实际问题中自变量的取值范围.知1-讲知1-讲例1 “黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子价格打8折.
(1)填写表.
(2)写出付款金额关于购买量的函数解析式,并画出
函数图象.知1-讲付款金额与种子价格相关. 问题中种子价格不是固
定不变的,它与购买量有关. 设购买x kg种子,当
0≤x≤2时,种子价格为5元/kg;当x>2时,其中有
2kg种子按5元/kg计价,其余的(x-2)kg(即超出2 kg
部分) 种子按4元/kg (即8折)计价,因此,写函数解析
式与画函数图象时,应对 0≤x≤2和x>2分段讨论.?分析:知1-讲(1)
解:(2)设购买量为xkg,付款金额为y元.
当0≤x≤2时,y=5x;
当x>2时,y=4(x-2)+10=4x+2.
函数图象如图 表格信息题是中考的热点题,解决表格问题的
关键是从表格中获取正确、易于解决问题的信息;
其建模的过程是:先设出函数的解析式,然后找出
两对对应值,列出二元一次方程组,求解即可得到
解析式.知1-讲1 —个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t (单位:h)的函数解析式,并画出函数图象.知1-练2 (2015·北京)一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550(元),若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A.购买A类会员年卡 B.购买B类会员年卡
C.购买C类会员年卡 D.不购买会员年卡知1-练2知识点用一次函数解含图象的实际问题知2-导思考
你能由上面的函数解析式解决以下问题吗?由函
数图象也能解决这些问题吗?
(1)一次购买1.5 kg种子,需付款多少元?
(2) 一次购买3 kg种子,需付款多少元? 利用函数方法解决实际问题,关键是分析题中的数
量关系,联系实际生活及以前学过的内容,将实际问题
抽象、升华为一次函数模型,即建模,再利用函数的性
质解决问题.一次函数的应用主要有两种类型:
(1)给出了一次函数解析式,直接应用一次函数的性质解
决问题;
(2)只用语言叙述或用表格、图象提供一次函数的情境时,
应先求出解析式,进而利用函数性质解决问题.知2-导知2-讲例2 某移动公司采用分段计费的方法
来计算话费,月通话时间x(min)
与相应话费y(元)之间的函数图象
如图.
(1)分别求出当0≤x<100和x≥100
时,y与x之间的函数解析式.
(2)月通话为280 min时,应交话费多少元?导引:本题是一道和话费有关的分段函数问题,通过图象可以
观察到,当0≤x<100时,y与x之间是正比例函数关系;
当x≥100时,y与x之间是一次函数关系,分别用待定系
数法可求得它们的解析式.知2-讲(1)当0≤x<100时,设y1=k1x(k1≠0),
将(100,40)代入得100k1=40,解得k1=
所以正比例函数的解析式为
当x≥100时,设y2=k2x+b(k2≠0),
将(100,40)及(200,60)分别代入得
所以一次函数解析式为 解:知2-讲因为280>100,
所以将x=280代入 中,得
即月通话时间为280 min时,应交话费76元.解:(2)月通话为280 min时,应交话费多少元? 分段函数中,自变量在不同的取值范围内的解
析式不同,在解决问题时,要特别注意自变量的取
值范围的变化.分段函数的应用面广,在水费、电
费、商品促销等领域都有广泛应用.本题考查一次
函数及识图能力,体现了数形结合思想.解决问题
的关键是由图象挖掘出有用的信息,利用待定系数
法先求出函数解析式,再解决问题.知2-讲1 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如图所示.这些农作物在第10天、第30天的需水量分别为2 000千克、3 000千克,在第40天后每天的需水量比前一天增加100千克.
(1)分别求出x≤40和x>40时y与x
之间的函数关系式;
(2)如果这些农作物每天的需水量
大于或等于4 000千克时需要进
行人工灌溉,那么应从第几天
开始进行人工灌溉?知2-练知2-练2 (2016·哈尔滨)明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每时完成的绿化面积是( )
A.300 m2
B.150 m2
C.330 m2
D.450 m21.运用一次函数解决实际问题的方法:
在日常生活和生产实践中有不少问题的数量关系可以
用一次函数来刻画.在运用一次函数解决实际问题时,
首先判断问题中的两个变量之间是不是一次函数关系,
当确定是一次函数关系时,求出函数解析式,并运用
一次函数的图象和性质进一步求得所需的结果.
说明:在应用一次函数的过程中,要注意结合实际,
确定自变量的取值范围,也要结合实际情况舍去不符
合题意的解.2.用一次函数解实际问题要明确“三点”
(1)一次函数关系的建立:一种是利用问题中变量间的相
等关系去列;另一种是在已知两个变量是一次函数关
系的情况下,用待定系数法去求.
(2)利用一次函数的值随自变量值的变化情况,在自变量
的取值范围内,求最大值或最小值.利用函数图象比
较大小.
(3)正确理解题意,读懂问题至关重要.我们可以通过画
图、联想实际情况等来帮助理解题意.
