19.2.8 一次函数与二元一次方程(组)课件
文档属性
| 名称 | 19.2.8 一次函数与二元一次方程(组)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 643.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 15:36:27 | ||
图片预览







文档简介
课件22张PPT。第8课时 一次函数与二元
一次方程(组)第十九章 一次函数19.2 一次函数1课堂讲解一次函数与二元一次方程的关系
一次函数与二元一次方程组的关系2课时流程逐点
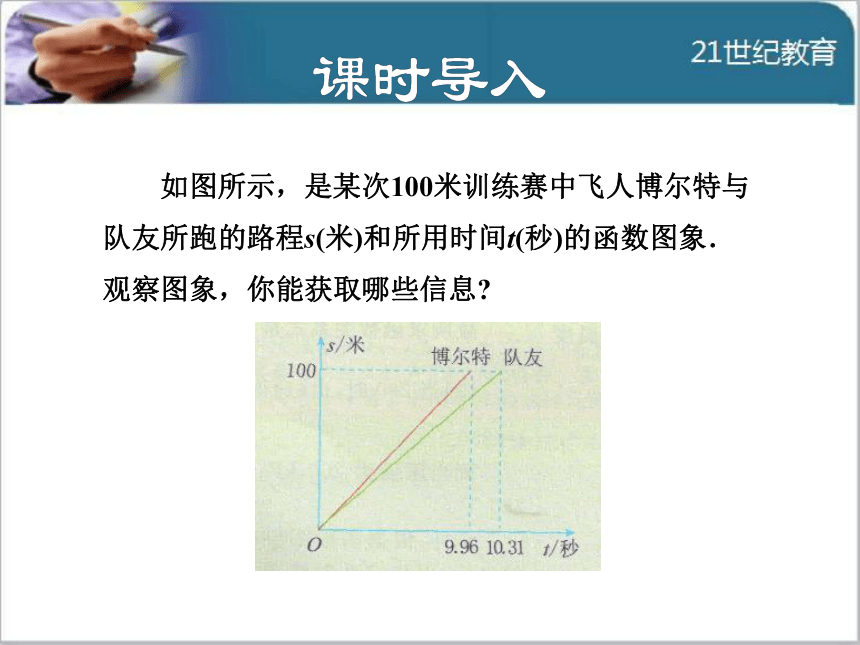
导讲练课堂小结作业提升 如图所示,是某次100米训练赛中飞人博尔特与
队友所跑的路程s(米)和所用时间t(秒)的函数图象.
观察图象,你能获取哪些信息?1知识点一次函数与二元一次方程的关系知1-讲二元一次方程与一次函数的联系
(1)任意一个二元一次方程都可化成y=kx+b的形式,
即令每个二元一次方程都对应一个一次函数,也
对应一条直线.
(2)直线y=kx+b上每一点的坐标均为这个二元一次
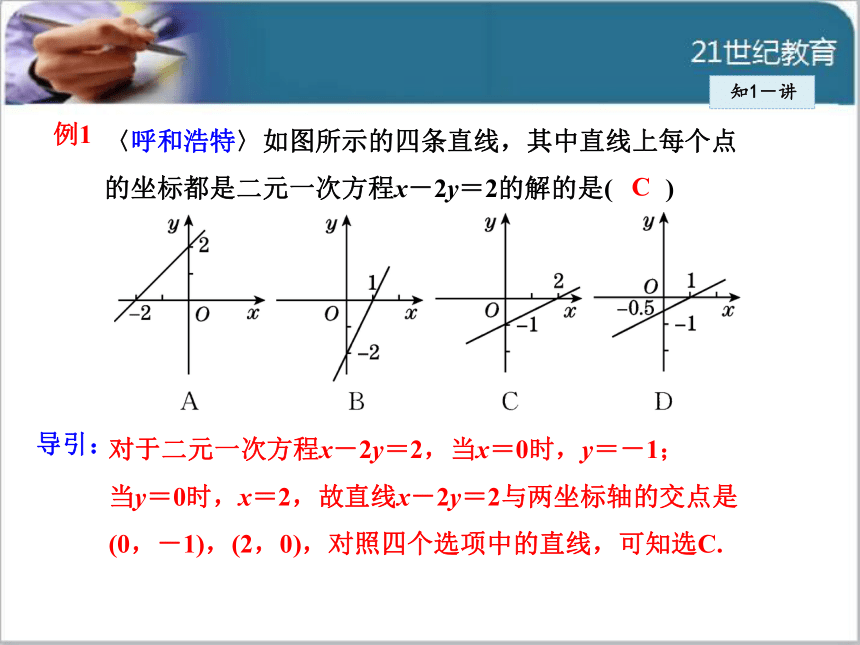
方程的解.知1-讲例1 〈呼和浩特〉如图所示的四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )导引:对于二元一次方程x-2y=2,当x=0时,y=-1;
当y=0时,x=2,故直线x-2y=2与两坐标轴的交点是
(0,-1),(2,0),对照四个选项中的直线,可知选C.C 直线y=kx+b与x轴的交点的横坐标即是二元一
次方程y=kx+b中,当y=0时x的值;
直线y=kx+b与y轴的交点的纵坐标即是二元一
次方程y=kx+b中,当x=0时y的值.
解这类题,常运用数形结合思想.知1-讲1〈济南〉一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
A.x=2
B.y=2
C.x=-1
D.y=-1知1-练2 直线y=kx+b(k≠0)对应的解析式就是一个关于x,y的________方程;以关于x,y的二元一次方程y-kx=b(k≠0)的解为坐标的点组成的图象就是一次函数________的图象.知1-练3 (中考·呼和浩特)以下四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )知1-练2知识点一次函数与二元一次方程组的关系知2-导问题
1号探测气球从海拔5m处出发,以1m/min的速度
上升.与此同时,2号探测气球从海拔15 m处出发,以
0.5 m/min的速度上升.两个气球都上升了1 h.
(1)用式子分别表示两个气球所在位置的海拔y (单位:m)
关于上升时间x(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这
时气球上升了多长时间?位于什么高度?知2-导(1)气球上升时间x满足0≤x≤60.
对于1号气球,y关于x的函数解析式为y=x+5.
对于2号气球,y关于x的函数解析式为y=0.5x+15.
(2)在某时刻两个气球位于同一高度,就是说对于x的
某个值 (0≤x≤60),函数y=x+5和y=0.5x+15有
相同的值y.如能求出这个x和y,则问题得到解决.
由此容易想到解二元一次方程组
这就是说,当上升20 min时,两个气球都位于海
拔25 m的高度.分析:知2-导 我们也可以用一次函数的图
象解释上述问题 的解答.如图,在
同一直角坐标系中,画出一次函
数y=x+5和y=0.5x+15的图象.
这两条直线的交点坐标为(20, 25),
这也说明当上升20 min时,两个
气球都位于海拔25 m的高度.
一般地,因为每个含有未知数x和y的二元一次方程,
都可以改写为y=kx+b(k、b是常数,k≠0)的形式,所以每
个这样的方程都对应一个一次函数,于是也对应一条直线.
这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.知2-导 由上可知,由含有未知数x和y的两个二元一次
方程组成的每个二元一 次方程组,都对应两个一次
函数,于是也对应两条直线.从“数”的角度看, 解
这样的方程组,相当于求自变量为何值时相应的两
个函数值相等,以及这个函数值是多少;从“形”
的角度看,解这样的方程组,相当于确定两条相应
直线交点的坐标.因此,我们可以用画一次函数图象
的方法得到方程组的解. 方程(组)与函数之间互相联系,从函数的角
度可以把它们统一起来.解决问题时,应根据具体
情况灵活地把它们结合起来考虑.知2-导知2-讲二元一次方程组与一次函数的关系:
(1)二元一次方程组中的每个方程均可看作函数解析式.
(2)求二元一次方程组的解可看作求两个一次函数的交
点坐标.知2-讲例2 利用图象法解二元一次方程组:解:列表得:
过点(0,-2)和(1,1)画出直线l1,
再过点(0,2)和(1,1)画出直线l2,如图,
由图象知:两条直线交点的坐标为(1,1),
∴方程组的解为: 用图象法解二元一次方程组的基本方法:
(1)将方程组中的两个方程转化成一次函数y=kx+b
的形式;
(2)在同一直角坐标系中画出两函数的图象;
(3)利用图象的直观性确定交点坐标.知2-讲1 直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组 请你直接写出它
的解;
(3)直线l3:y=nx+m是否也
经过点P?请说明理由.知2-练知2-练2 两条直线y=k1x+b1和y=k2x+b2相交于点A(4,-5),
则方程组 的解是( )
A. B.
C. D.知2-练3 若一次函数y=k1x+b1与y=k2x+b2的图象没有交
点,则方程组 的解的情况是( )
A.有无数个解 B.有两个解
C.只有一个解 D.没有解1. 二元一次方程组无解?一次函数的图象平行(无交点);
二元一次方程组有一组解?一次函数的图象相交(有
一个交点);
二元一次方程组有无数个解?一次函数的图象重合(有
无数个交点).2. 二元一次方程与一次函数之间的区别和联系
区别:
(1)二元一次方程有两个未知数.而一次函数有两个变量;
(2)二元一次方程是用一个等式表示两个未 知数的关系.
而一次函数既可以用一个等式表示两个变量之间的关
系.又可以用表格或图象来表示两个变量之间的关系.
联系:
在直角坐标系中分别描出以二元一次方程的解为坐标的
点.这些点都在相应的一次函数的图象上.
一次方程(组)第十九章 一次函数19.2 一次函数1课堂讲解一次函数与二元一次方程的关系
一次函数与二元一次方程组的关系2课时流程逐点
导讲练课堂小结作业提升 如图所示,是某次100米训练赛中飞人博尔特与
队友所跑的路程s(米)和所用时间t(秒)的函数图象.
观察图象,你能获取哪些信息?1知识点一次函数与二元一次方程的关系知1-讲二元一次方程与一次函数的联系
(1)任意一个二元一次方程都可化成y=kx+b的形式,
即令每个二元一次方程都对应一个一次函数,也
对应一条直线.
(2)直线y=kx+b上每一点的坐标均为这个二元一次
方程的解.知1-讲例1 〈呼和浩特〉如图所示的四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )导引:对于二元一次方程x-2y=2,当x=0时,y=-1;
当y=0时,x=2,故直线x-2y=2与两坐标轴的交点是
(0,-1),(2,0),对照四个选项中的直线,可知选C.C 直线y=kx+b与x轴的交点的横坐标即是二元一
次方程y=kx+b中,当y=0时x的值;
直线y=kx+b与y轴的交点的纵坐标即是二元一
次方程y=kx+b中,当x=0时y的值.
解这类题,常运用数形结合思想.知1-讲1〈济南〉一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
A.x=2
B.y=2
C.x=-1
D.y=-1知1-练2 直线y=kx+b(k≠0)对应的解析式就是一个关于x,y的________方程;以关于x,y的二元一次方程y-kx=b(k≠0)的解为坐标的点组成的图象就是一次函数________的图象.知1-练3 (中考·呼和浩特)以下四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )知1-练2知识点一次函数与二元一次方程组的关系知2-导问题
1号探测气球从海拔5m处出发,以1m/min的速度
上升.与此同时,2号探测气球从海拔15 m处出发,以
0.5 m/min的速度上升.两个气球都上升了1 h.
(1)用式子分别表示两个气球所在位置的海拔y (单位:m)
关于上升时间x(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这
时气球上升了多长时间?位于什么高度?知2-导(1)气球上升时间x满足0≤x≤60.
对于1号气球,y关于x的函数解析式为y=x+5.
对于2号气球,y关于x的函数解析式为y=0.5x+15.
(2)在某时刻两个气球位于同一高度,就是说对于x的
某个值 (0≤x≤60),函数y=x+5和y=0.5x+15有
相同的值y.如能求出这个x和y,则问题得到解决.
由此容易想到解二元一次方程组
这就是说,当上升20 min时,两个气球都位于海
拔25 m的高度.分析:知2-导 我们也可以用一次函数的图
象解释上述问题 的解答.如图,在
同一直角坐标系中,画出一次函
数y=x+5和y=0.5x+15的图象.
这两条直线的交点坐标为(20, 25),
这也说明当上升20 min时,两个
气球都位于海拔25 m的高度.
一般地,因为每个含有未知数x和y的二元一次方程,
都可以改写为y=kx+b(k、b是常数,k≠0)的形式,所以每
个这样的方程都对应一个一次函数,于是也对应一条直线.
这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.知2-导 由上可知,由含有未知数x和y的两个二元一次
方程组成的每个二元一 次方程组,都对应两个一次
函数,于是也对应两条直线.从“数”的角度看, 解
这样的方程组,相当于求自变量为何值时相应的两
个函数值相等,以及这个函数值是多少;从“形”
的角度看,解这样的方程组,相当于确定两条相应
直线交点的坐标.因此,我们可以用画一次函数图象
的方法得到方程组的解. 方程(组)与函数之间互相联系,从函数的角
度可以把它们统一起来.解决问题时,应根据具体
情况灵活地把它们结合起来考虑.知2-导知2-讲二元一次方程组与一次函数的关系:
(1)二元一次方程组中的每个方程均可看作函数解析式.
(2)求二元一次方程组的解可看作求两个一次函数的交
点坐标.知2-讲例2 利用图象法解二元一次方程组:解:列表得:
过点(0,-2)和(1,1)画出直线l1,
再过点(0,2)和(1,1)画出直线l2,如图,
由图象知:两条直线交点的坐标为(1,1),
∴方程组的解为: 用图象法解二元一次方程组的基本方法:
(1)将方程组中的两个方程转化成一次函数y=kx+b
的形式;
(2)在同一直角坐标系中画出两函数的图象;
(3)利用图象的直观性确定交点坐标.知2-讲1 直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组 请你直接写出它
的解;
(3)直线l3:y=nx+m是否也
经过点P?请说明理由.知2-练知2-练2 两条直线y=k1x+b1和y=k2x+b2相交于点A(4,-5),
则方程组 的解是( )
A. B.
C. D.知2-练3 若一次函数y=k1x+b1与y=k2x+b2的图象没有交
点,则方程组 的解的情况是( )
A.有无数个解 B.有两个解
C.只有一个解 D.没有解1. 二元一次方程组无解?一次函数的图象平行(无交点);
二元一次方程组有一组解?一次函数的图象相交(有
一个交点);
二元一次方程组有无数个解?一次函数的图象重合(有
无数个交点).2. 二元一次方程与一次函数之间的区别和联系
区别:
(1)二元一次方程有两个未知数.而一次函数有两个变量;
(2)二元一次方程是用一个等式表示两个未 知数的关系.
而一次函数既可以用一个等式表示两个变量之间的关
系.又可以用表格或图象来表示两个变量之间的关系.
联系:
在直角坐标系中分别描出以二元一次方程的解为坐标的
点.这些点都在相应的一次函数的图象上.
