20.1.2 用样本平均数估计总体平均数课件
文档属性
| 名称 | 20.1.2 用样本平均数估计总体平均数课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 699.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 19:08:06 | ||
图片预览






文档简介
课件29张PPT。第二十章 数据的分析20.1 数据的集中趋势第2课时 用样本平均数估
计总体平均数1课堂讲解加权平均数(用个数表示的“权”)
用组中值(用频数表示“权”)求平均数用样本估计总体2课时流程逐点
导讲练课堂小结作业提升 在篮球比赛中,队员的身高是反映球队实力的一
个重要因素,如何衡量两个球队从员的身高?怎样理
解“甲队队员的身高比乙队更高”?要比较两个球队
队员的身高,需要收集哪些数据呢?1知识点加权平均数(用个数表示的“权”)知1-讲 在求n个数的平均数时,如果x1出现f1次,x2出现f2次,
…,xk出现fk次(这里f1+f2+…+fk=n),那么这n个
数的平均数 也叫做x1,x2,
…,xk这k个数的加权平均数,其中f1,f2,…,fk分
别叫做x1,x2,…,xk的权.某跳水队为了解运动员的年龄情况,作了一次年龄调
查,结果如 下:13岁8人,14岁16人,15岁24人,16
岁2人.求这个跳水队运动员的 平均年龄(结果取整数).知1-讲例1 解:这个跳水队运动员的平均年龄为知1-讲 平均成绩应该等于总年龄数除以总人数,由于
各个年龄段的人数不相同,因此它们的“权”不相
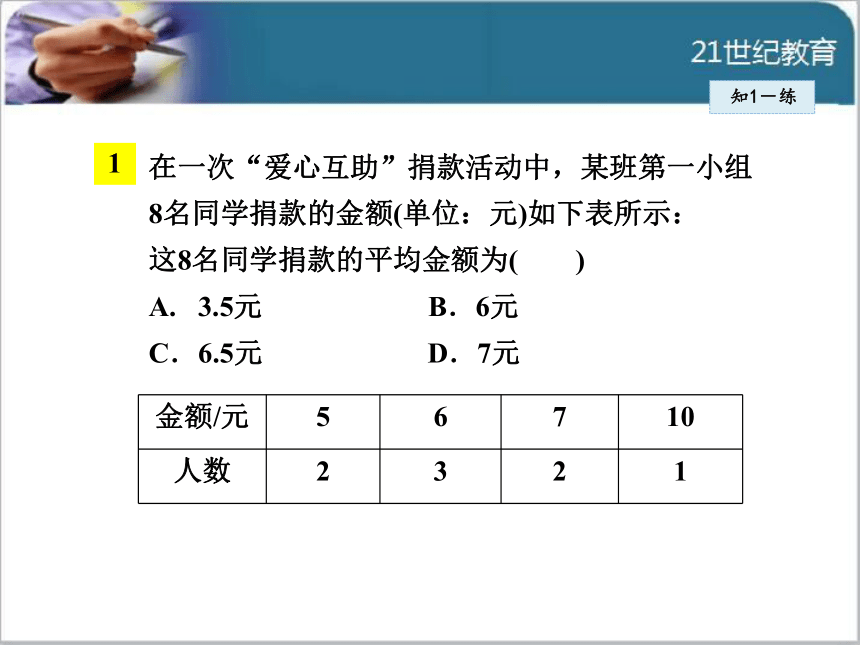
同,所以应该用加权平均数公式求解.知1-练在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如下表所示:
这8名同学捐款的平均金额为( )
A. 3.5元 B.6元
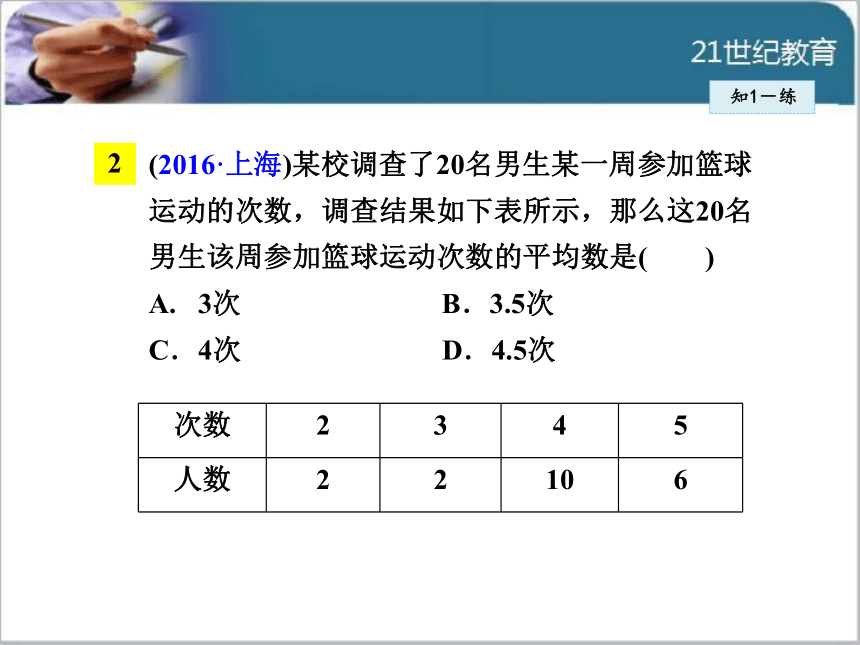
C.6.5元 D.7元知1-练(2016·上海)某校调查了20名男生某一周参加篮球运动的次数,调查结果如下表所示,那么这20名男生该周参加篮球运动次数的平均数是( )
A. 3次 B.3.5次
C.4次 D.4.5次
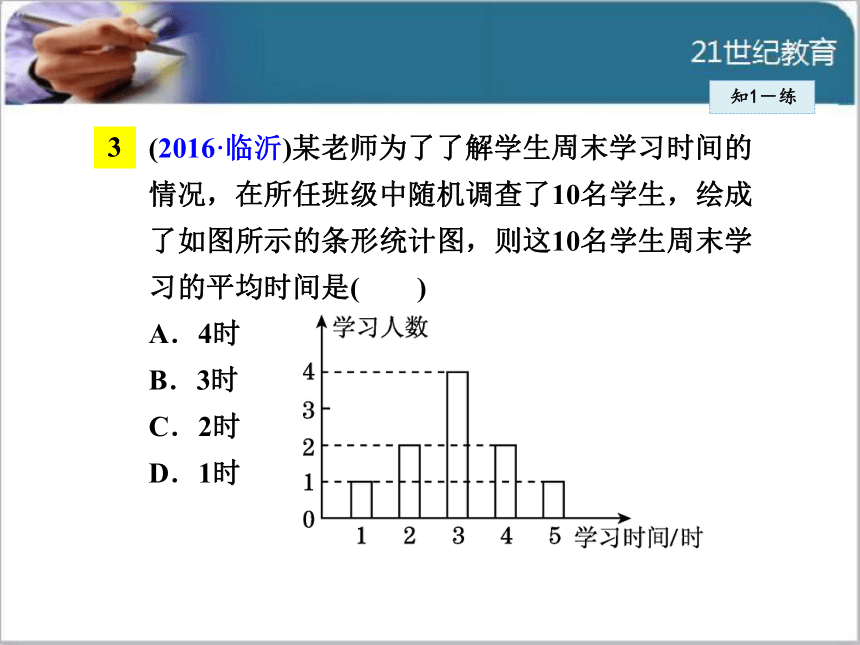
知1-练(2016·临沂)某老师为了了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成了如图所示的条形统计图,则这10名学生周末学习的平均时间是( )
A.4时
B.3时
C.2时
D.1时2知识点用组中值(用频数表示“权”)求平均数知2-讲探究
为了解5路公共汽车的运菅情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表. 这天5路公共汽车平均每班的载客 量是多少(结
果取整数)?知2-讲知2-讲 根据上面的频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组
的频数看作相应组中值的权. 例如在1≤x<21之间的
载客量近似地看作组中值11,组中值11的权是它的
频数3. 因此这天5路公共汽车平均每班的载客量是知2-讲为了了解某县八年级女生的身高情况,在该县某校八年级女生中随机抽测了200名女生的身高,统计数据如下:例2知2-讲知2-讲请你结合所给数据,回答下列问题:
(1)表中的P=________,Q=________;
(2)请把如图所示的直方图补充完整;(1)由统计图可以看出:
P=60,Q=200-50-60-70=20;
(2)根据(1)中Q的值作图即可.导引:解:(2)如图所示:6020知2-讲(3)这200名女生的平均身高大约为________.(3)分别求出每组的组中值,则200名女生的平均
身高为
因此这200名女生的平均身高大约为153 cm.导引:153 cm知2-讲 根据频数分布表或频数分布直方图来计算加权平
均数的方法:
统计中常用各组数据的组中值代表各组的实际数
据,把各组中的频数看成是相应组中值的权来进行计
算,特别说明:数据分组后,一个小组的组中值是指
这个小组的两个端点的数的平均数.知2-练某校为了了解本校八年级学生一天中做作业所用的时间的情况,随机抽查了本校八年级的30名学生,并把调查所得的所有数据(时间,都为整数)进行整理,分成五组,绘制成频数分布直方图(如图).请结合图中所提供的信息,回答下列问题:
(1)被抽查的学生中做作业所用的
时间在90.5分钟到120.5分钟范
围的人数是多少?
(2)补全频数分布直方图;
(3)估计被抽查的学生做作业所用
的平均时间(精确到个位).知2-练下列各组数据中,组中值不是10的是( )
A.0≤x<20
B.8≤x<12
C.7≤x<13
D.3≤x<7知2-练对一组数据进行了整理,结果如下表:
则这组数据的平均数约是( )
A.10 B.11 C.12 D.16知2-练王老师对八(1)班的某次考试成绩进行统计后,绘制了频数分布直方图(如图,分数取正整数,满分120分).根据图中信息填空:
(1)该班有________名学生;
(2)89.5~99.5这一组的频数是________;
(3)估计该班这次考试的平均成绩是________.3知识点用样本估计总体知3-讲 我们知道,当所要考察的对象很多,或者对考
察对象带有破坏性时,统计中常常通过用样本估计
总体的方法来获得对总体的认识 . 例如,实际生活
中经常用样本的平均数来估计总体的平均数.知3-讲要点精析:
(1)用样本估计总体时,样本容量越大,样本对总体
的估计越准确,相应的工作量及破坏性也大,因
此样本容量的确定,既要考虑问题本身的需要,
又要考虑实现的可能性及付出的代价.
(2)抽取的样本要具有一般性和代表性.知3-讲某灯泡厂为测量一批灯泡的使用寿命,从中随机抽
查了 50只灯泡. 它们的使用寿命如表所示.这批灯泡
的平均使用寿命是多少?例3 知3-讲抽出的50只灯泡的使用寿命组成一个样本. 可以
利用样本的平均使用寿命来估计这批灯泡的平均
使用寿命.
根据上表, 可以得出各小组的组中值,于是分析:解:即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大
约是 1 672 h.知3-练种菜能手李大叔种植了一批新品种黄瓜 . 为了考察这种黄瓜的生长情况,他随机抽查了部分黄瓜藤上长出的黄瓜根数,得到右面的条形图. 请估计这个新品种黄瓜平均每株结多少根黄瓜(结果取整数).知3-练(2016·黄石)黄石农科所在相同条件下经试验发现蚕
豆种子的发芽率为97.1%,请估计黄石地区1 000斤
蚕豆种子中不能发芽的大约有( )
A.971斤
B.129斤
C.97.1斤
D.29斤知3-练(2015·镇江)有4万个不小于70的两位数,从中随机抽取3 000个数据,统计如下:
请根据表格中的信息,估计这4万个数据的平均数为( )
A.92.16 B.85.23 C.84.73 D.77.97利用频数分布表求加权平均数时,统计中常用各
组的组中值代表各组实际的数据,把各组的频数
看成是相应组中值的权,从而算出平均数.
2. 当所要考察的对象很多,或考察过程带有破坏性
的时候,统计中常用样本平均数去估计总体平均
数.
计总体平均数1课堂讲解加权平均数(用个数表示的“权”)
用组中值(用频数表示“权”)求平均数用样本估计总体2课时流程逐点
导讲练课堂小结作业提升 在篮球比赛中,队员的身高是反映球队实力的一
个重要因素,如何衡量两个球队从员的身高?怎样理
解“甲队队员的身高比乙队更高”?要比较两个球队
队员的身高,需要收集哪些数据呢?1知识点加权平均数(用个数表示的“权”)知1-讲 在求n个数的平均数时,如果x1出现f1次,x2出现f2次,
…,xk出现fk次(这里f1+f2+…+fk=n),那么这n个
数的平均数 也叫做x1,x2,
…,xk这k个数的加权平均数,其中f1,f2,…,fk分
别叫做x1,x2,…,xk的权.某跳水队为了解运动员的年龄情况,作了一次年龄调
查,结果如 下:13岁8人,14岁16人,15岁24人,16
岁2人.求这个跳水队运动员的 平均年龄(结果取整数).知1-讲例1 解:这个跳水队运动员的平均年龄为知1-讲 平均成绩应该等于总年龄数除以总人数,由于
各个年龄段的人数不相同,因此它们的“权”不相
同,所以应该用加权平均数公式求解.知1-练在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如下表所示:
这8名同学捐款的平均金额为( )
A. 3.5元 B.6元
C.6.5元 D.7元知1-练(2016·上海)某校调查了20名男生某一周参加篮球运动的次数,调查结果如下表所示,那么这20名男生该周参加篮球运动次数的平均数是( )
A. 3次 B.3.5次
C.4次 D.4.5次
知1-练(2016·临沂)某老师为了了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成了如图所示的条形统计图,则这10名学生周末学习的平均时间是( )
A.4时
B.3时
C.2时
D.1时2知识点用组中值(用频数表示“权”)求平均数知2-讲探究
为了解5路公共汽车的运菅情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表. 这天5路公共汽车平均每班的载客 量是多少(结
果取整数)?知2-讲知2-讲 根据上面的频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组
的频数看作相应组中值的权. 例如在1≤x<21之间的
载客量近似地看作组中值11,组中值11的权是它的
频数3. 因此这天5路公共汽车平均每班的载客量是知2-讲为了了解某县八年级女生的身高情况,在该县某校八年级女生中随机抽测了200名女生的身高,统计数据如下:例2知2-讲知2-讲请你结合所给数据,回答下列问题:
(1)表中的P=________,Q=________;
(2)请把如图所示的直方图补充完整;(1)由统计图可以看出:
P=60,Q=200-50-60-70=20;
(2)根据(1)中Q的值作图即可.导引:解:(2)如图所示:6020知2-讲(3)这200名女生的平均身高大约为________.(3)分别求出每组的组中值,则200名女生的平均
身高为
因此这200名女生的平均身高大约为153 cm.导引:153 cm知2-讲 根据频数分布表或频数分布直方图来计算加权平
均数的方法:
统计中常用各组数据的组中值代表各组的实际数
据,把各组中的频数看成是相应组中值的权来进行计
算,特别说明:数据分组后,一个小组的组中值是指
这个小组的两个端点的数的平均数.知2-练某校为了了解本校八年级学生一天中做作业所用的时间的情况,随机抽查了本校八年级的30名学生,并把调查所得的所有数据(时间,都为整数)进行整理,分成五组,绘制成频数分布直方图(如图).请结合图中所提供的信息,回答下列问题:
(1)被抽查的学生中做作业所用的
时间在90.5分钟到120.5分钟范
围的人数是多少?
(2)补全频数分布直方图;
(3)估计被抽查的学生做作业所用
的平均时间(精确到个位).知2-练下列各组数据中,组中值不是10的是( )
A.0≤x<20
B.8≤x<12
C.7≤x<13
D.3≤x<7知2-练对一组数据进行了整理,结果如下表:
则这组数据的平均数约是( )
A.10 B.11 C.12 D.16知2-练王老师对八(1)班的某次考试成绩进行统计后,绘制了频数分布直方图(如图,分数取正整数,满分120分).根据图中信息填空:
(1)该班有________名学生;
(2)89.5~99.5这一组的频数是________;
(3)估计该班这次考试的平均成绩是________.3知识点用样本估计总体知3-讲 我们知道,当所要考察的对象很多,或者对考
察对象带有破坏性时,统计中常常通过用样本估计
总体的方法来获得对总体的认识 . 例如,实际生活
中经常用样本的平均数来估计总体的平均数.知3-讲要点精析:
(1)用样本估计总体时,样本容量越大,样本对总体
的估计越准确,相应的工作量及破坏性也大,因
此样本容量的确定,既要考虑问题本身的需要,
又要考虑实现的可能性及付出的代价.
(2)抽取的样本要具有一般性和代表性.知3-讲某灯泡厂为测量一批灯泡的使用寿命,从中随机抽
查了 50只灯泡. 它们的使用寿命如表所示.这批灯泡
的平均使用寿命是多少?例3 知3-讲抽出的50只灯泡的使用寿命组成一个样本. 可以
利用样本的平均使用寿命来估计这批灯泡的平均
使用寿命.
根据上表, 可以得出各小组的组中值,于是分析:解:即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大
约是 1 672 h.知3-练种菜能手李大叔种植了一批新品种黄瓜 . 为了考察这种黄瓜的生长情况,他随机抽查了部分黄瓜藤上长出的黄瓜根数,得到右面的条形图. 请估计这个新品种黄瓜平均每株结多少根黄瓜(结果取整数).知3-练(2016·黄石)黄石农科所在相同条件下经试验发现蚕
豆种子的发芽率为97.1%,请估计黄石地区1 000斤
蚕豆种子中不能发芽的大约有( )
A.971斤
B.129斤
C.97.1斤
D.29斤知3-练(2015·镇江)有4万个不小于70的两位数,从中随机抽取3 000个数据,统计如下:
请根据表格中的信息,估计这4万个数据的平均数为( )
A.92.16 B.85.23 C.84.73 D.77.97利用频数分布表求加权平均数时,统计中常用各
组的组中值代表各组实际的数据,把各组的频数
看成是相应组中值的权,从而算出平均数.
2. 当所要考察的对象很多,或考察过程带有破坏性
的时候,统计中常用样本平均数去估计总体平均
数.
