20.2.1 方差课件
图片预览








文档简介
课件29张PPT。第二十章 数据的分析20.2 数据的波动程度第1课时 方差1课堂讲解方差的意义
方差的求法
方差的应用2课时流程逐点
导讲练课堂小结作业提升 在统计学中,除了平均数、中位数、众数这类刻画数
据集中趋势的量以外,还有一类刻画数据波动(离散)程
度的量,其中最重要的就是方差. 本节我们将在实际问题
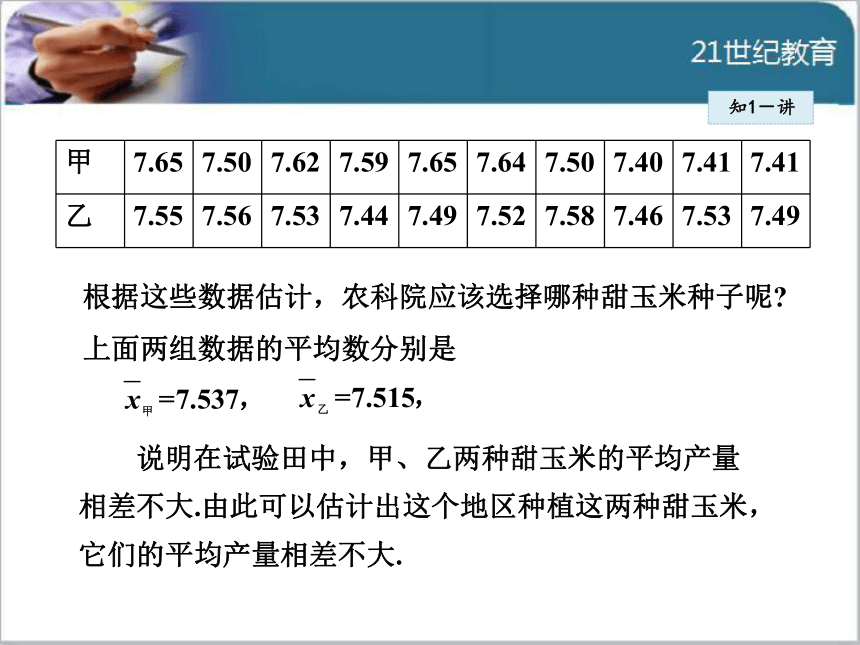
情境中,了解方差的统计意义并运用方差解决问题.1知识点方差的意义知1-讲问题 农科院计划为某地选择合适的甜玉米种子.选择
种子时,甜玉米的产量和产量的稳定性是农科院所关
心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10块自然条件相同的试验田进行试验,得
到各试验田每公顷的产量 (单位:t) 如下表所示.知1-讲根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
上面两组数据的平均数分别是 说明在试验田中,甲、乙两种甜玉米的平均产量
相差不大.由此可以估计出这个地区种植这两种甜玉米,
它们的平均产量相差不大.知1-讲为了直观地看出甲、乙两种甜玉米产量的情况,我们把
这两组数据画成下面的图20.2-1和图20.2-2.知1-讲 比较上面的两幅图可以看出,甲种甜玉米在各
试验田的产量波动较大, 乙 种甜玉米在各试验田的
产量较集中地分布在平均产量附近. 从图中看出的
结果能否用一个量来刻画呢?知1-讲 为了刻画一组数据波动的大小,可以采用很多
方法. 统计中常采用下面的 做法:设有n个数据x1,
x2 ,… ,xn,各数据与它们的平均数 的差的平方
分别是 … ,
我们用这些值的平均数,即用
来衡量这组数据波动的大小,并把它叫做这组数据
的方差(variance),记作s2.知1-讲定义:设有n个数据x1,x2,…,xn ,各数据与它们
的平均数 的差的平方分别是
… , 我们用这些值的平均数,即用
来衡量这组数据波动的大小,并把它叫做这组数据
的方差(variance),记作s2.知1-讲要点精析:
(1)方差是用来衡量一组数据的波动大小的重要量,
反映的是数据在平均数附近波动的情况;
(2)对于同类问题的两组数据,方差越大,数据的
波动就越大;方差越小,数据的波动就越小.知1-讲人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:
=80,s2甲=240,s2乙=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定例1 B知1-讲在本题中,给出平均分和方差两种数据,那么平
均分要考查的是甲、乙两班的成绩的优劣,而成
绩的稳定性就要看两班成绩的方差了.那么所谓
的稳定性,也就是指成绩的波动.成绩波动越小,
成绩越稳定.根据“方差越大,数据的波动越大:
方差越小,数据的波动越小,我们很容易发现乙
班的方差比甲班的小,所以乙班的成绩较稳定.分析:知1-讲 在利用方差比较两组数据的波动情况时,一定要先
计算两组数据的平均数.一般说来,平均数可能反映数
据的优劣程度,如果在平均数上已经能够区分几组数据
的优劣,那么就不用再考虑方差的大小了.但在实际的
习题中,往往都是平均值相同,那么此时就要考虑数据
的方差情况了.由此可得到:在解决问题时,要先算平
均数,当平均值不同时,择优选取;当平均数相同时,
比较方差,选择波动较小的一组数据.知1-练(2015·广州)两名同学各进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.众数 B.中位数
C.方差 D.以上都不对知1-练(2015·乌鲁木齐)在某次射击训练中,甲、乙、丙、丁4人各射击10次,平均成绩相同,方差分别是
s甲2=0.35,s乙2=0.15,s丙2=0.25,s丁2=0.27,这4人中成绩发挥最稳定的是( )
A.甲 B.乙
C.丙 D.丁2知识点方差的求法知2-讲方差的计算方法
设有n个数据x1,x2,…,xn .
(1)计算这组数据的平均数 ;
(2)求各数据与它们的平均数的差的平方:
… ,
(3)求(2)中这n个数据的平均数,记为s2.则方差的计
算公式为:s2= 知2-讲在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅 湖》, 参加表演的女演员的身高(单位:cm)如表所示.
哪个芭蕾舞团女演员的身高更整齐?例2 知2-讲甲、乙两团演员的身高平均数分别是解:方差分别是由s甲2 < s乙2 可知,甲芭蕾舞团女演员的身高
更整齐.知2-讲 一般地,设n个数据x1,x2,…,xn的平均数为
,则方差
s2=
它反映了一组数据的波动大小,方差越大,波动性
越大,反之也成立.知2-练〈威海〉在某中学举行的演讲比赛中,初一年级5名
参赛选手的成绩如下表所示,请你根据表中提供的
数据,计算出这5名选手成绩的方差是( )
A. 2 B.6.8
C.34 D.93知2-练(2016·龙岩)在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错的是( )
A.平均数为160 B.中位数为158
C.众数为158 D.方差为20.3知2-练(2016·永州)在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8,7,9,8,8 乙:7,9,6,9,9
则下列说法中错误的是( )
A.甲、乙得分的平均数是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小知3-讲3知识点方差的应用某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品 加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定 通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机 抽取15个,记录它们的质量(单位:g)如表所示.根据表中数据,你 认为快餐公司应该选购哪家加工厂的鸡腿?例3知3-讲检查人员从甲、乙两家农副产品加工厂各随机抽取的15
个鸡腿分别组成一个样本,样本数据的平均数分别是解:知3-讲样本数据的方差分别是 由 可知,两家加工厂的鸡腿质量大致相
等;由s甲2 < s乙2可知,甲加工厂的鸡腿质量更稳定,
大小更均匀. 因此,快餐公司应该选购甲加工厂生
产的鸡腿.知3-讲 在比较两组数据时,一般先看平均数,在平均
数相同或相近的情况下,再分析稳定性问题,而方
差是反映数据的波动大小的量,通过比较方差的大
小来解决问题.知3-练某跳远队准备从甲、乙两名运动员中选取成绩稳
定的一名参加比赛. 下表是这两名运动员10次测
验成绩(单位:m)
你认为应该选择哪名运动员参赛?为什么?知3-练(2015·来宾)在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①s甲2>s乙2;②s甲2A.①③
B.①④
C.②③
D.②④1.方差是用来衡量一组数据波动大小的重要统计量,反映
的是数据在平均数附近波动的情况,对于同类问题的两
组数据,方差越大,数据波动就越大,方差越小,数据
波动就越小;在统计中常用样本方差去估计总体方差.
2.一组数据的每一个数据都加上或减去同一个常数,所得
新数据的方差与原数据的方差相等.
3.一组数据的每一个数据都变为原数据的k倍,则所得新数
据的方差变为原数据方差的k2倍.
方差的求法
方差的应用2课时流程逐点
导讲练课堂小结作业提升 在统计学中,除了平均数、中位数、众数这类刻画数
据集中趋势的量以外,还有一类刻画数据波动(离散)程
度的量,其中最重要的就是方差. 本节我们将在实际问题
情境中,了解方差的统计意义并运用方差解决问题.1知识点方差的意义知1-讲问题 农科院计划为某地选择合适的甜玉米种子.选择
种子时,甜玉米的产量和产量的稳定性是农科院所关
心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10块自然条件相同的试验田进行试验,得
到各试验田每公顷的产量 (单位:t) 如下表所示.知1-讲根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
上面两组数据的平均数分别是 说明在试验田中,甲、乙两种甜玉米的平均产量
相差不大.由此可以估计出这个地区种植这两种甜玉米,
它们的平均产量相差不大.知1-讲为了直观地看出甲、乙两种甜玉米产量的情况,我们把
这两组数据画成下面的图20.2-1和图20.2-2.知1-讲 比较上面的两幅图可以看出,甲种甜玉米在各
试验田的产量波动较大, 乙 种甜玉米在各试验田的
产量较集中地分布在平均产量附近. 从图中看出的
结果能否用一个量来刻画呢?知1-讲 为了刻画一组数据波动的大小,可以采用很多
方法. 统计中常采用下面的 做法:设有n个数据x1,
x2 ,… ,xn,各数据与它们的平均数 的差的平方
分别是 … ,
我们用这些值的平均数,即用
来衡量这组数据波动的大小,并把它叫做这组数据
的方差(variance),记作s2.知1-讲定义:设有n个数据x1,x2,…,xn ,各数据与它们
的平均数 的差的平方分别是
… , 我们用这些值的平均数,即用
来衡量这组数据波动的大小,并把它叫做这组数据
的方差(variance),记作s2.知1-讲要点精析:
(1)方差是用来衡量一组数据的波动大小的重要量,
反映的是数据在平均数附近波动的情况;
(2)对于同类问题的两组数据,方差越大,数据的
波动就越大;方差越小,数据的波动就越小.知1-讲人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:
=80,s2甲=240,s2乙=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定例1 B知1-讲在本题中,给出平均分和方差两种数据,那么平
均分要考查的是甲、乙两班的成绩的优劣,而成
绩的稳定性就要看两班成绩的方差了.那么所谓
的稳定性,也就是指成绩的波动.成绩波动越小,
成绩越稳定.根据“方差越大,数据的波动越大:
方差越小,数据的波动越小,我们很容易发现乙
班的方差比甲班的小,所以乙班的成绩较稳定.分析:知1-讲 在利用方差比较两组数据的波动情况时,一定要先
计算两组数据的平均数.一般说来,平均数可能反映数
据的优劣程度,如果在平均数上已经能够区分几组数据
的优劣,那么就不用再考虑方差的大小了.但在实际的
习题中,往往都是平均值相同,那么此时就要考虑数据
的方差情况了.由此可得到:在解决问题时,要先算平
均数,当平均值不同时,择优选取;当平均数相同时,
比较方差,选择波动较小的一组数据.知1-练(2015·广州)两名同学各进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.众数 B.中位数
C.方差 D.以上都不对知1-练(2015·乌鲁木齐)在某次射击训练中,甲、乙、丙、丁4人各射击10次,平均成绩相同,方差分别是
s甲2=0.35,s乙2=0.15,s丙2=0.25,s丁2=0.27,这4人中成绩发挥最稳定的是( )
A.甲 B.乙
C.丙 D.丁2知识点方差的求法知2-讲方差的计算方法
设有n个数据x1,x2,…,xn .
(1)计算这组数据的平均数 ;
(2)求各数据与它们的平均数的差的平方:
… ,
(3)求(2)中这n个数据的平均数,记为s2.则方差的计
算公式为:s2= 知2-讲在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅 湖》, 参加表演的女演员的身高(单位:cm)如表所示.
哪个芭蕾舞团女演员的身高更整齐?例2 知2-讲甲、乙两团演员的身高平均数分别是解:方差分别是由s甲2 < s乙2 可知,甲芭蕾舞团女演员的身高
更整齐.知2-讲 一般地,设n个数据x1,x2,…,xn的平均数为
,则方差
s2=
它反映了一组数据的波动大小,方差越大,波动性
越大,反之也成立.知2-练〈威海〉在某中学举行的演讲比赛中,初一年级5名
参赛选手的成绩如下表所示,请你根据表中提供的
数据,计算出这5名选手成绩的方差是( )
A. 2 B.6.8
C.34 D.93知2-练(2016·龙岩)在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错的是( )
A.平均数为160 B.中位数为158
C.众数为158 D.方差为20.3知2-练(2016·永州)在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8,7,9,8,8 乙:7,9,6,9,9
则下列说法中错误的是( )
A.甲、乙得分的平均数是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小知3-讲3知识点方差的应用某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品 加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定 通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机 抽取15个,记录它们的质量(单位:g)如表所示.根据表中数据,你 认为快餐公司应该选购哪家加工厂的鸡腿?例3知3-讲检查人员从甲、乙两家农副产品加工厂各随机抽取的15
个鸡腿分别组成一个样本,样本数据的平均数分别是解:知3-讲样本数据的方差分别是 由 可知,两家加工厂的鸡腿质量大致相
等;由s甲2 < s乙2可知,甲加工厂的鸡腿质量更稳定,
大小更均匀. 因此,快餐公司应该选购甲加工厂生
产的鸡腿.知3-讲 在比较两组数据时,一般先看平均数,在平均
数相同或相近的情况下,再分析稳定性问题,而方
差是反映数据的波动大小的量,通过比较方差的大
小来解决问题.知3-练某跳远队准备从甲、乙两名运动员中选取成绩稳
定的一名参加比赛. 下表是这两名运动员10次测
验成绩(单位:m)
你认为应该选择哪名运动员参赛?为什么?知3-练(2015·来宾)在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①s甲2>s乙2;②s甲2
B.①④
C.②③
D.②④1.方差是用来衡量一组数据波动大小的重要统计量,反映
的是数据在平均数附近波动的情况,对于同类问题的两
组数据,方差越大,数据波动就越大,方差越小,数据
波动就越小;在统计中常用样本方差去估计总体方差.
2.一组数据的每一个数据都加上或减去同一个常数,所得
新数据的方差与原数据的方差相等.
3.一组数据的每一个数据都变为原数据的k倍,则所得新数
据的方差变为原数据方差的k2倍.
