26.1.3 反比例函数的几何性质 课件
文档属性
| 名称 | 26.1.3 反比例函数的几何性质 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 211.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 23:49:57 | ||
图片预览






文档简介
(共20张PPT)
第二十六章 反比例函数
26.1 反比例函数
第3课时 反比例函数的几何
性质
1
课堂讲解
反比例函数中k的几何性质
反比例函数图象的对称性
2
课时流程
逐点
导讲练
课堂小结
作业提升
问题情境:
反比例函数解析式 图象 位置 增减性
(k>0) 第一、三象限 在每个象限内,y随x的增大而减小
(k<0) 第二、四象限 在每个象限内,y随x的增大而增大
1
知识点
反比例函数中k的几何性质
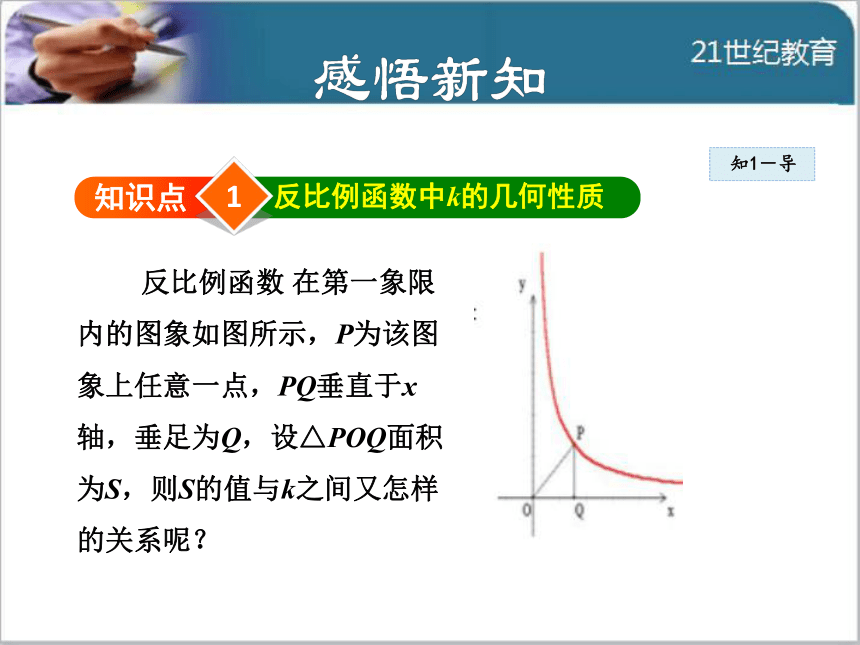
反比例函数 在第一象限
内的图象如图所示,P为该图
象上任意一点,PQ垂直于x
轴,垂足为Q,设△POQ面积
为S,则S的值与k之间又怎样
的关系呢?
知1-导
知1-导
归 纳
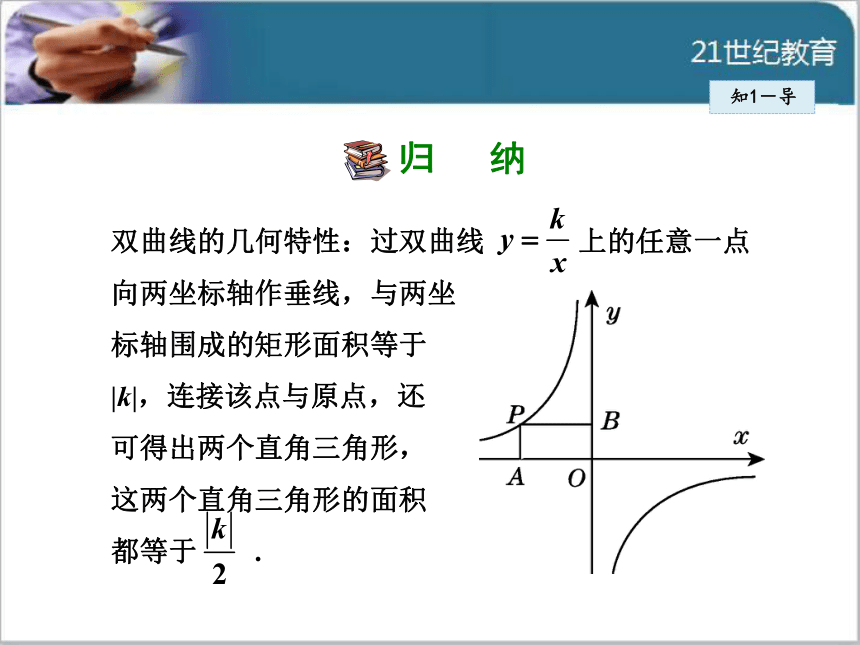
双曲线的几何特性:过双曲线 上的任意一点
向两坐标轴作垂线,与两坐
标轴围成的矩形面积等于
|k|,连接该点与原点,还
可得出两个直角三角形,
这两个直角三角形的面积
都等于 .
例1〈永州〉如图,两个反比例函数 和
在第一象限内的图象分别是C1和C2,设点P在C1
上,PA⊥x轴于点A,交C2于点B,则△POB的面
积为________.
导引:根据反比例函数中
k的几何意义,得△POA
和△BOA的面积分别为2
和1,于是阴影部分的面
积为1.
知1-讲
1
总 结
知1-讲
求阴影部分面积的方法:
当它无法直接求出时,一般都采用“转化”的
方法,将它转化为易求图形面积的和或差来进行计
算.如本例就是将阴影部分面积转化为两个与比例
系数相关的特殊三角形的面积的差来求,要注意转
化思想的运用.
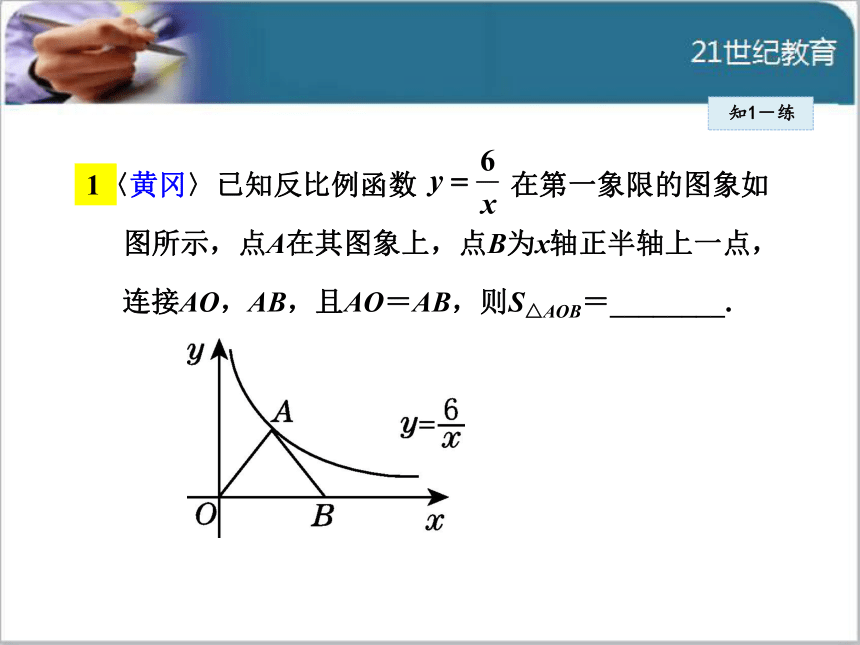
1〈黄冈〉已知反比例函数 在第一象限的图象如
图所示,点A在其图象上,点B为x轴正半轴上一点,
连接AO,AB,且AO=AB,则S△AOB=________.
知1-练
2.(2016·河南)如图,过反比例函数 (x>0)的
图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB
=2,则k的值为( )
A.2
B.3
C.4
D.5
知1-练
3.(2016·沈阳)如图,在平面直角坐标系中,点P是反
比例函数 (x>0)图象上的一点,分别过点P
作PA⊥x轴于点A,PB⊥y轴于点B.若四边形OAPB
的面积为3,则k的值为( )
A.3 B.-3
C. D.
知1-练
2
知识点
反比例函数图象的对称性
知2-讲
反比例函数的图象关于原点成中心对称,也就
是把它的图象旋转180°与原图形重合,这是反比例
函数的一个重要性质,就常用来求点的坐标和图形
的面积等
知2-讲
例2〈白银〉如图,在直角坐标系xOy中,直线y=mx与
双曲线 相交于A(-1,a),B两点,BC⊥x
轴,垂足为C,△AOC的面积是1.
(1)求m,n的值;
(2)求直线AC对应的函数解析式.
知2-讲
导引:(1)由题意,根据对称性得到点B的横坐标为1,确定
出点C的坐标,根据△AOC的面积求出点A的纵坐标,
确定出点A的坐标,将点A的坐标代入正比例函数与
反比例函数解析式,即可求出m与n的值;
(2)设直线AC对应的函数解析式为y=kx+b,将A,C
两点坐标分别代入求出k与b的值,即可确定出直线
AC对应的函数解析式.
知2-讲
解:(1)∵直线y=mx与双曲线 相交于A(-1,a),
B两点,
∴B点横坐标为1.
∴C(1,0).
∵△AOC的面积为1,
∴ ×a×1=1,∴a=2,
∴A(-1,2).
将A(-1,2)的坐标代入y=mx,
可得m=-2,n=-2.
知2-讲
(2)设直线AC对应的函数解析式为y=kx+b,
∵直线y=kx+b经过点A(-1,2),C(1,0),
∴ 解得
∴直线AC对应的函数解析式为y=-x+1.
总 结
知2-讲
反比例函数与正比例函数的图象都是中心对称
图形,所以在同一坐标系中,两个函数图象的两个交
点关于原点对称.
1 〈山西〉已知直线y=ax(a≠0)与双曲线 (k≠0)
的一个交点的坐标为(2,6),则它们的另一个交点的坐
标是( )
A.(-2,6) B.(-6,-2)
C.(-2,-6) D.(6,2)
知2-练
若 +|b-2|=0,点P(a,b)在反比例函数
的图象上,则这个函数的图象位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
知2-练
知2-练
(2015·钦州)对于函数 ,下列说法错误的是 ( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称
图形
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
1.反比例函数中k的几何性质:过双曲线 (k≠0)
上任一点向两坐标轴作垂线所得的矩形面积等于|k|;
向一坐标轴作垂线且与原点连线所得的三角形面积等
于 |k|.
2.双曲线关于直线y=x和直线y=-x成轴对称.
第二十六章 反比例函数
26.1 反比例函数
第3课时 反比例函数的几何
性质
1
课堂讲解
反比例函数中k的几何性质
反比例函数图象的对称性
2
课时流程
逐点
导讲练
课堂小结
作业提升
问题情境:
反比例函数解析式 图象 位置 增减性
(k>0) 第一、三象限 在每个象限内,y随x的增大而减小
(k<0) 第二、四象限 在每个象限内,y随x的增大而增大
1
知识点
反比例函数中k的几何性质
反比例函数 在第一象限
内的图象如图所示,P为该图
象上任意一点,PQ垂直于x
轴,垂足为Q,设△POQ面积
为S,则S的值与k之间又怎样
的关系呢?
知1-导
知1-导
归 纳
双曲线的几何特性:过双曲线 上的任意一点
向两坐标轴作垂线,与两坐
标轴围成的矩形面积等于
|k|,连接该点与原点,还
可得出两个直角三角形,
这两个直角三角形的面积
都等于 .
例1〈永州〉如图,两个反比例函数 和
在第一象限内的图象分别是C1和C2,设点P在C1
上,PA⊥x轴于点A,交C2于点B,则△POB的面
积为________.
导引:根据反比例函数中
k的几何意义,得△POA
和△BOA的面积分别为2
和1,于是阴影部分的面
积为1.
知1-讲
1
总 结
知1-讲
求阴影部分面积的方法:
当它无法直接求出时,一般都采用“转化”的
方法,将它转化为易求图形面积的和或差来进行计
算.如本例就是将阴影部分面积转化为两个与比例
系数相关的特殊三角形的面积的差来求,要注意转
化思想的运用.
1〈黄冈〉已知反比例函数 在第一象限的图象如
图所示,点A在其图象上,点B为x轴正半轴上一点,
连接AO,AB,且AO=AB,则S△AOB=________.
知1-练
2.(2016·河南)如图,过反比例函数 (x>0)的
图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB
=2,则k的值为( )
A.2
B.3
C.4
D.5
知1-练
3.(2016·沈阳)如图,在平面直角坐标系中,点P是反
比例函数 (x>0)图象上的一点,分别过点P
作PA⊥x轴于点A,PB⊥y轴于点B.若四边形OAPB
的面积为3,则k的值为( )
A.3 B.-3
C. D.
知1-练
2
知识点
反比例函数图象的对称性
知2-讲
反比例函数的图象关于原点成中心对称,也就
是把它的图象旋转180°与原图形重合,这是反比例
函数的一个重要性质,就常用来求点的坐标和图形
的面积等
知2-讲
例2〈白银〉如图,在直角坐标系xOy中,直线y=mx与
双曲线 相交于A(-1,a),B两点,BC⊥x
轴,垂足为C,△AOC的面积是1.
(1)求m,n的值;
(2)求直线AC对应的函数解析式.
知2-讲
导引:(1)由题意,根据对称性得到点B的横坐标为1,确定
出点C的坐标,根据△AOC的面积求出点A的纵坐标,
确定出点A的坐标,将点A的坐标代入正比例函数与
反比例函数解析式,即可求出m与n的值;
(2)设直线AC对应的函数解析式为y=kx+b,将A,C
两点坐标分别代入求出k与b的值,即可确定出直线
AC对应的函数解析式.
知2-讲
解:(1)∵直线y=mx与双曲线 相交于A(-1,a),
B两点,
∴B点横坐标为1.
∴C(1,0).
∵△AOC的面积为1,
∴ ×a×1=1,∴a=2,
∴A(-1,2).
将A(-1,2)的坐标代入y=mx,
可得m=-2,n=-2.
知2-讲
(2)设直线AC对应的函数解析式为y=kx+b,
∵直线y=kx+b经过点A(-1,2),C(1,0),
∴ 解得
∴直线AC对应的函数解析式为y=-x+1.
总 结
知2-讲
反比例函数与正比例函数的图象都是中心对称
图形,所以在同一坐标系中,两个函数图象的两个交
点关于原点对称.
1 〈山西〉已知直线y=ax(a≠0)与双曲线 (k≠0)
的一个交点的坐标为(2,6),则它们的另一个交点的坐
标是( )
A.(-2,6) B.(-6,-2)
C.(-2,-6) D.(6,2)
知2-练
若 +|b-2|=0,点P(a,b)在反比例函数
的图象上,则这个函数的图象位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
知2-练
知2-练
(2015·钦州)对于函数 ,下列说法错误的是 ( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称
图形
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
1.反比例函数中k的几何性质:过双曲线 (k≠0)
上任一点向两坐标轴作垂线所得的矩形面积等于|k|;
向一坐标轴作垂线且与原点连线所得的三角形面积等
于 |k|.
2.双曲线关于直线y=x和直线y=-x成轴对称.
