26.1.4 反比例函数的图象与性质的应用 课件
文档属性
| 名称 | 26.1.4 反比例函数的图象与性质的应用 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 339.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 23:51:37 | ||
图片预览








文档简介
(共26张PPT)
第二十六章 反比例函数
26.1 反比例函数
第4课时 反比例函数的图象与
性质的应用
1
题型
图表信息题
1.数学复习课上,王老师出示了如框中的题目:
已知直线y=kx+b(k≠0,b≠0)经过点M(b,-b),
求证:点M一定在双曲线 上.
题目中的黑色矩形框部分是一段被墨水污染了无法辨认
的文字.
(1)根据已知和结论中现有的信息,你能否求出题中直线对
应的函数解析式?若能,请写出求解过程;若不能,请
说明理由.
(2)请你根据已有的信息,在原题的黑色矩形框中,添加一
个适当的条件,把原题补充完整.你添加的这个条件是
什么?
解:(1)能.
由结论中的点M一定在双曲线 上,得
则b=-2,∴M(-2,2).
∴2=-2k-2.解得k=-2.
∴直线对应的函数解析式为y=-2x-2.
(2)答案不唯一,
如:直线y=kx+b经过点N(1,-4)等等.
(1)把点M的坐标代入双曲线对应的函数解析式中得到关于b的方程,解该方程即可求出b的值,从而求得M的坐标,代入直线对应的函数解析式即可求得k的值,从而求得一次函数的解析式;(2)根据(1)中所求的函数解析式可写出图象上另一个点的坐标,添加的条件不唯一.
2
题型
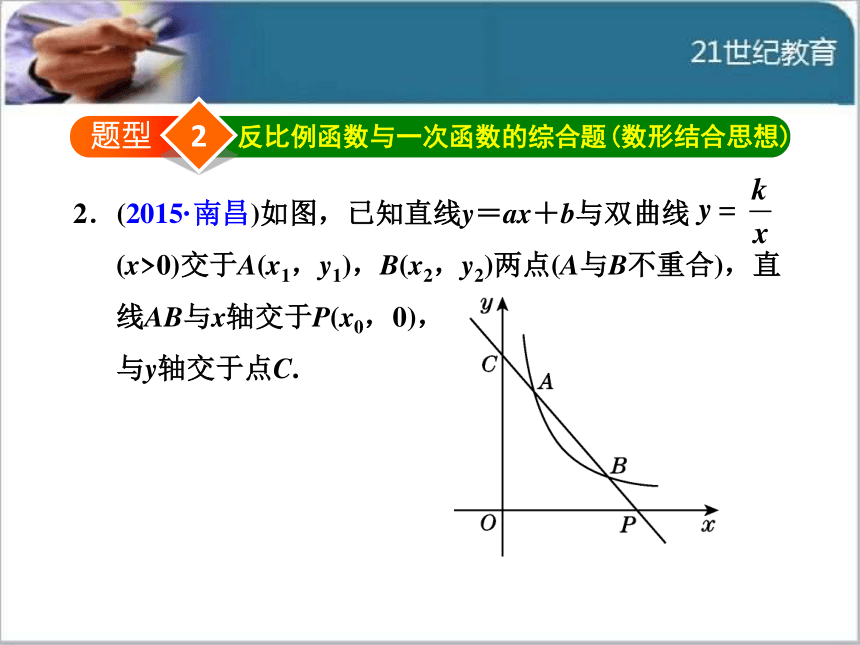
反比例函数与一次函数的综合题(数形结合思想)
2.(2015·南昌)如图,已知直线y=ax+b与双曲线
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直
线AB与x轴交于P(x0,0),
与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的
坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求
A,B两点的坐标;
(3)结合(1)(2)中的结果,猜想并用等式表示x1,x2,x0
之间的关系.(不要求证明)
解:(1)把A(1,3)的坐标代入 ,得k=3.
∴反比例函数解析式为
∵点(3,y2)也在双曲线上,
∴3y2=3,y2=1.
把A(1,3),B(3,1)的坐标分别代入y=ax+b,
得 解得
∴一次函数解析式为y=-x+4.
当y=0时,x=4,
∴点P的坐标为(4,0).
(2)如图,作AD⊥x轴于点D,BE⊥x轴于点E,得AD∥BE,
AD=y1,BE=y2.∵AB=BP,
∴BE= AD,即y2= y1,DE=EP.
∵A(x1,y1),B(x2,y2)都在双曲线 上,
∴x1y1=x2y2=k.∴2x1=x2,
OD=DE=x1.
∴OD=DE=EP=x1.
由点P(6,0),知OP=6,
∴3x1=6,x1=2.∴x2=2x1=4.
∵b=y1+1,y1=ax1+b,
∴ 解得a=
∴一次函数解析式为y= x+b.
∴y1=-1+b,y2=-2+b.
又∵y2= y1,∴b=3.
∴一次函数的解析式为y= x+3.
∴A(2,2),B(4,1).
(3)x1+x2=x0.
3
题型
函数与几何的综合题
3.(2015·济宁)在矩形AOBC中,OB=6,OA=4,分别以OB,
OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,
F是边BC上一点(不与B,C两点重合),过点F的反比例函数
(k>0)的图象与AC边交于点E.
(1)请用含k的式子表示
点E,F的坐标;
(2)若△OEF的面积为9,
求反比例函数的解析
式.
解:(1)E F
(2)∵E,F两点的坐标分别为
∴S△ECF= EC·CF= (6- k) (4- k).
∴S△EOF=S矩形AOBC-S△AOE-S△BOF-S△ECF
=24- k- k-S△ECF
=24-k- (6- k) (4- k).
∵△OEF的面积为9,
∴24-k- (6- k) (4- k)=9.
整理得,k2=144,k=±12.
∵k>0,∴k=12.
∴反比例函数的解析式为
4
题型
一次函数、反比例函数、三角形面积的综合题
4.(2015·山西)如图,在平面直角坐标系xOy中,一次函数y=
3x+2的图象与y轴交于点A,与反比例函数 (k≠0)在
第一象限内的图象交于点B,且点B的横坐标为1.过点A作
AC⊥y轴交反比例函数 (k≠0)的图象于点C,连接BC.
求:
(1)反比例函数的解析式;
(2)△ABC的面积.
解:(1)∵一次函数y=3x+2的图象过点B,
且点B的横坐标为1,
∴y=3×1+2=5.
∴点B的坐标为(1,5).
∵点B在反比例函数 的图象上,
∴k=1×5=5.
∴反比例函数的解析式为
(2)∵一次函数y=3x+2的图象与y轴交于点A,
当x=0时,y=2,
∴点A的坐标为(0,2).
∵AC⊥y轴,
∴点C的纵坐标与点A的纵坐标相同,是2.
∵点C在反比例函数 的图象上,
∴当y=2时, 解得
∴AC=
如图,过点B作BD⊥AC于D,
则BD=yB-yC=5-2=3,
∴S△ABC= AC·BD
= × ×3
=
5
题型
反比例函数与中心对称
5.(2016·株洲)如图,平行四边形ABCD的两个顶点A,C在反
比例函数 (k≠0)图象上,点B,D在x轴上,且B,D
两点关于原点对称,AD交y轴于P点.
(1)已知点A的坐标是(2,3),
求k的值及C点的坐标;
(2)若△APO的面积为2,求
点D到直线AC的距离.
解:(1)∵点A的坐标是(2,3),且点A在反比例函数
(k≠0)图象上,
∴ ∴k=6,
又∵点C与点A关于原点O对称,
∴C(-2,-3).
(2)∵△APO的面积为2,点A的坐标是(2,3),
∴2= ,得OP=2,
∴点P的坐标为(0,2).
设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,
∴ 解得
即直线PA对应函数的解析式为y= x+2.
将y=0代入y= x+2,得x=-4,
∴OD=4,
∵A(2,3),C(-2,-3),
∴AC=
设点D到AC的距离为m,
∵S△ACD=S△ODA+S△ODC,
∴
解得m= ,即点D到直线AC的距离是
6
题型
反比例函数与轴对称的综合题
6. (2015·南通)如图,直线y=mx+n与双曲线 相交于
A(-1,2),B(2,b)两点,与y轴相交于点C.
(1)求m,n的值;
(2)若点D与点C关于x轴
对称,求△ABD的面
积.
解:(1)把x=-1,y=2;x=2,y=b代入
解得k=-2,b=-1;
把x=-1,y=2;x=2,y=-1代入y=mx+n,
解得m=-1,n=1.
(2)直线y=-x+1与y轴交点C的坐标为(0,1),所以
点D的坐标为(0,-1).又点B的坐标为(2,-1),
点A的坐标为(-1,2),
所以△ABD的面积= ×2×(1+2)=3.
7
题型
反比例函数与几何最小值的综合题
7.如图,反比例函数 (k≠0,x>0)的图象与直线y=3x
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比
例函数图象于点D,且AB=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,
使点M到C,D两点距
离之和d=MC+MD最小,求点M的坐标.
解:(1)∵A(1,3),∴OB=1,AB=3.
又∵AB=3BD,∴BD=1,
∴D(1,1).∴k=1×1=1.
(2)由(1)知反比例函数的解析式为
解方程组 得 或 (舍去).
∴点C的坐标为
(3)如图,作点D关于y轴的对称点E,则E(-1,1),作直
线CE,交y轴于点M,点M即为所求.设直线CE对应
的函数解析式为y=mx+b,则
解得
∴直线CE对应的函数解析式为
y=(2 -3)x+2 -2.
当x=0时,y=2 -2,
∴点M的坐标为(0,2 -2).
第二十六章 反比例函数
26.1 反比例函数
第4课时 反比例函数的图象与
性质的应用
1
题型
图表信息题
1.数学复习课上,王老师出示了如框中的题目:
已知直线y=kx+b(k≠0,b≠0)经过点M(b,-b),
求证:点M一定在双曲线 上.
题目中的黑色矩形框部分是一段被墨水污染了无法辨认
的文字.
(1)根据已知和结论中现有的信息,你能否求出题中直线对
应的函数解析式?若能,请写出求解过程;若不能,请
说明理由.
(2)请你根据已有的信息,在原题的黑色矩形框中,添加一
个适当的条件,把原题补充完整.你添加的这个条件是
什么?
解:(1)能.
由结论中的点M一定在双曲线 上,得
则b=-2,∴M(-2,2).
∴2=-2k-2.解得k=-2.
∴直线对应的函数解析式为y=-2x-2.
(2)答案不唯一,
如:直线y=kx+b经过点N(1,-4)等等.
(1)把点M的坐标代入双曲线对应的函数解析式中得到关于b的方程,解该方程即可求出b的值,从而求得M的坐标,代入直线对应的函数解析式即可求得k的值,从而求得一次函数的解析式;(2)根据(1)中所求的函数解析式可写出图象上另一个点的坐标,添加的条件不唯一.
2
题型
反比例函数与一次函数的综合题(数形结合思想)
2.(2015·南昌)如图,已知直线y=ax+b与双曲线
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直
线AB与x轴交于P(x0,0),
与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的
坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求
A,B两点的坐标;
(3)结合(1)(2)中的结果,猜想并用等式表示x1,x2,x0
之间的关系.(不要求证明)
解:(1)把A(1,3)的坐标代入 ,得k=3.
∴反比例函数解析式为
∵点(3,y2)也在双曲线上,
∴3y2=3,y2=1.
把A(1,3),B(3,1)的坐标分别代入y=ax+b,
得 解得
∴一次函数解析式为y=-x+4.
当y=0时,x=4,
∴点P的坐标为(4,0).
(2)如图,作AD⊥x轴于点D,BE⊥x轴于点E,得AD∥BE,
AD=y1,BE=y2.∵AB=BP,
∴BE= AD,即y2= y1,DE=EP.
∵A(x1,y1),B(x2,y2)都在双曲线 上,
∴x1y1=x2y2=k.∴2x1=x2,
OD=DE=x1.
∴OD=DE=EP=x1.
由点P(6,0),知OP=6,
∴3x1=6,x1=2.∴x2=2x1=4.
∵b=y1+1,y1=ax1+b,
∴ 解得a=
∴一次函数解析式为y= x+b.
∴y1=-1+b,y2=-2+b.
又∵y2= y1,∴b=3.
∴一次函数的解析式为y= x+3.
∴A(2,2),B(4,1).
(3)x1+x2=x0.
3
题型
函数与几何的综合题
3.(2015·济宁)在矩形AOBC中,OB=6,OA=4,分别以OB,
OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,
F是边BC上一点(不与B,C两点重合),过点F的反比例函数
(k>0)的图象与AC边交于点E.
(1)请用含k的式子表示
点E,F的坐标;
(2)若△OEF的面积为9,
求反比例函数的解析
式.
解:(1)E F
(2)∵E,F两点的坐标分别为
∴S△ECF= EC·CF= (6- k) (4- k).
∴S△EOF=S矩形AOBC-S△AOE-S△BOF-S△ECF
=24- k- k-S△ECF
=24-k- (6- k) (4- k).
∵△OEF的面积为9,
∴24-k- (6- k) (4- k)=9.
整理得,k2=144,k=±12.
∵k>0,∴k=12.
∴反比例函数的解析式为
4
题型
一次函数、反比例函数、三角形面积的综合题
4.(2015·山西)如图,在平面直角坐标系xOy中,一次函数y=
3x+2的图象与y轴交于点A,与反比例函数 (k≠0)在
第一象限内的图象交于点B,且点B的横坐标为1.过点A作
AC⊥y轴交反比例函数 (k≠0)的图象于点C,连接BC.
求:
(1)反比例函数的解析式;
(2)△ABC的面积.
解:(1)∵一次函数y=3x+2的图象过点B,
且点B的横坐标为1,
∴y=3×1+2=5.
∴点B的坐标为(1,5).
∵点B在反比例函数 的图象上,
∴k=1×5=5.
∴反比例函数的解析式为
(2)∵一次函数y=3x+2的图象与y轴交于点A,
当x=0时,y=2,
∴点A的坐标为(0,2).
∵AC⊥y轴,
∴点C的纵坐标与点A的纵坐标相同,是2.
∵点C在反比例函数 的图象上,
∴当y=2时, 解得
∴AC=
如图,过点B作BD⊥AC于D,
则BD=yB-yC=5-2=3,
∴S△ABC= AC·BD
= × ×3
=
5
题型
反比例函数与中心对称
5.(2016·株洲)如图,平行四边形ABCD的两个顶点A,C在反
比例函数 (k≠0)图象上,点B,D在x轴上,且B,D
两点关于原点对称,AD交y轴于P点.
(1)已知点A的坐标是(2,3),
求k的值及C点的坐标;
(2)若△APO的面积为2,求
点D到直线AC的距离.
解:(1)∵点A的坐标是(2,3),且点A在反比例函数
(k≠0)图象上,
∴ ∴k=6,
又∵点C与点A关于原点O对称,
∴C(-2,-3).
(2)∵△APO的面积为2,点A的坐标是(2,3),
∴2= ,得OP=2,
∴点P的坐标为(0,2).
设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,
∴ 解得
即直线PA对应函数的解析式为y= x+2.
将y=0代入y= x+2,得x=-4,
∴OD=4,
∵A(2,3),C(-2,-3),
∴AC=
设点D到AC的距离为m,
∵S△ACD=S△ODA+S△ODC,
∴
解得m= ,即点D到直线AC的距离是
6
题型
反比例函数与轴对称的综合题
6. (2015·南通)如图,直线y=mx+n与双曲线 相交于
A(-1,2),B(2,b)两点,与y轴相交于点C.
(1)求m,n的值;
(2)若点D与点C关于x轴
对称,求△ABD的面
积.
解:(1)把x=-1,y=2;x=2,y=b代入
解得k=-2,b=-1;
把x=-1,y=2;x=2,y=-1代入y=mx+n,
解得m=-1,n=1.
(2)直线y=-x+1与y轴交点C的坐标为(0,1),所以
点D的坐标为(0,-1).又点B的坐标为(2,-1),
点A的坐标为(-1,2),
所以△ABD的面积= ×2×(1+2)=3.
7
题型
反比例函数与几何最小值的综合题
7.如图,反比例函数 (k≠0,x>0)的图象与直线y=3x
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比
例函数图象于点D,且AB=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,
使点M到C,D两点距
离之和d=MC+MD最小,求点M的坐标.
解:(1)∵A(1,3),∴OB=1,AB=3.
又∵AB=3BD,∴BD=1,
∴D(1,1).∴k=1×1=1.
(2)由(1)知反比例函数的解析式为
解方程组 得 或 (舍去).
∴点C的坐标为
(3)如图,作点D关于y轴的对称点E,则E(-1,1),作直
线CE,交y轴于点M,点M即为所求.设直线CE对应
的函数解析式为y=mx+b,则
解得
∴直线CE对应的函数解析式为
y=(2 -3)x+2 -2.
当x=0时,y=2 -2,
∴点M的坐标为(0,2 -2).
