27.1.2 相似多边形课件
图片预览







文档简介
课件24张PPT。第二十七章 相 似27.1 图形的相似第2课时 相似多边形1课堂讲解相似多边形
相似多边形的性质
相似比2课时流程逐点
导讲练课堂小结作业提升 你看上边的图形有何特点呢?今天我们就来研究
这个问题!1知识点相似多边形问 题知1-导 图中的两个大小不同的四边形
ABCD和四边形A1B1C1D1中,∠A=
∠A1,∠B=∠B1,∠C=∠C1,∠D
=∠D1, ,因此四边形ABCD与四边
形A1B1C1D1相似.知1-导定义:如果两个多边形的角分别相等,边成比例,那
么这两个多边形叫做相似多边形.
判定相似多边形的条件:
(1)所有的角分别相等;
(2)所有的边成比例.
以上的角分别相等,边成比例这两个条件是判定相
似多边形必备的条件,缺一不可.例1 如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,
GF⊥AB,垂足分别为点E,F.
求证:四边形AFGE与四边形ABCD相似.知1-讲导引:要判定两个多边形相似,从边和角两个方面
证明,即需证对应角相等,对应边的比相等.
证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠DAC
=∠BAC=45°.又∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG.
∴AE=EG=FG=AF,∴四边形AFGE为正方形.
∴ ,且∠EAF=∠DAB,
∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE与四边形ABCD相似.知1-讲 判断两个多边形是否相似,既要看它们的角是否
分别相等,也要看边是否成比例,两者缺一不可.例
如:两个矩形不一定相似,两个菱形也不一定相似,
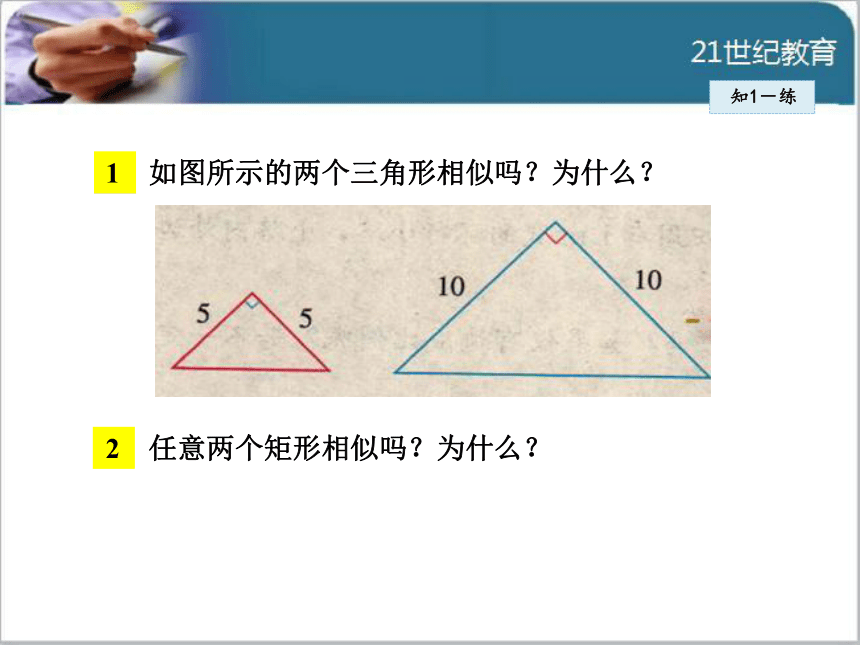
两个正方形一定相似.1 如图所示的两个三角形相似吗?为什么?
2 任意两个矩形相似吗?为什么? 知1-练甲:将边长为3,4,5的三角形按图①的方式向
外扩张,得到新三角形,它们的对应边间距均
为1,则新三角形与原三角形相似.
乙:将邻边长为3和5的矩形按图②的方式向外
扩张,得到新矩形,它们的对应边间距均为1,
则新矩形与原矩形不相似.3 (中考·河北)在研究相似问题时,甲、乙同学的观点
如下:
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.甲对,乙不对 D.甲不对,乙对知1-练4 放大镜中的多边形与原多边形的关系是( )
A.形状不同,大小不同
B.形状相同,大小相同
C.形状相同,大小不同
D.形状不同,大小相同知1-练2知识点相似多边形的性质知2-导 如图的左边格点图中有一
个四边形,请在右边的格点图
中画出一个与该四边形相似的
图形.问 题 1 对于图中两个相似的四边形,它们的对应角,对应
边的比是否相等.问 题 2知识点知2-讲 图中的两个大小不同的四边形
ABCD和四边形A1B1C1D1中,
∠A=∠A1,∠B=∠B1,∠C=
∠C1,∠D=∠D1, ,因此四边形
ABCD与四边形A1B1C1D1相似.
由相似多边形的定义可知,相似多边形的对应角相
等,对应边成比例.知2-讲相似多边形的性质:相似多边形的对应边的比相等,
对应角相等.
作用:常用来求相似多边形中未知的边的长度和角的
度数.知2-讲例2 如图,四边形ABCD和EFGH相似,求角α,β的大
小和EF的长度x.解:因为四边形ABCD和EFGH相
似,所以它们的对应角相等,
由此可得α=∠C=83°, ∠A=∠E=118°.
在四边形ABCD中,
β=360°-(78°+83°+118°) = 81°.
因为四边形ABCD和EFGH相似,所以它们的对应边
成比例,由此可得
解得x=28. 知2-讲 利用相似多边形的性质求边长或角度,关键扣住
“对应”二字,找准对应边和对应角是解决问题的关
键.需要注意的是对应边是比相等,而对应角是直接
相等.1 如图所示的两个五边形相似,求a,b,c,
d的值.知2-练知2-练2 如图所示的两个四边形相似,则α的度数是( )
A.87° B.60° C.75° D.120°
3 一个多边形的边长分别为2,3,4,5,6,另一个多
边形和这个多边形相似,且最短边长为6,则最长边
长为( )
A.18 B.12 C.24 D.30知3-导3知识点相似比 两个图形相似,其中一个图形可以看作
由另一个图形放大或缩小得到.例如,放映电
影时,投在屏幕上的画面就是胶片上图形的
放大;用复印机把一个图形放大或缩小后所
得的图形,都与原来的图形相似.图中有2对图
形,每对图形中的两个图形相似.其中较大(小)的图形可以看成是
由较小(大)的图形放大(缩小)得到的.
上边的图形是相似图形,它们对应的比值有何关系呢?我
们用尺子测量一下,看看.通过测量,我们发现每两个图形对
应边的比值相等,我们把相似多边形对应边的比称为相似比.知3-导相似比的定义:相似多边形对应边的比称为相似比.
要点精析:
(1)相似比与两个多边形的前后顺序有关;
(2)相似比为1的两个相似多边形为全等多边形.知3-讲导引:相似多边形的对应边的比相等,其比值就是相似比.
解:(1)设AD=x,则DM= .∵矩形DMNC与矩形ABCD相似,
∴x2=32.
∴x=4 或x=-4 (舍去),即AD的长为4 .
(2)矩形DMNC与矩形ABCD的相似比为例3 如图,把矩形ABCD对折,折痕为MN,矩形DMNC与
矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.知3-讲 利用相似多边形的性质求线段长及相似比的方法:
先找出与已知边、未知边相关的四条对应线段,再通过
设未知数并用含未知数的式子表示其中的部分线段,最
后通过相似多边形的对应边成比例建立方程进行计算.
这种巧用方程思想的方法在相似多边形的计算中经常
运用.1 如图,DE ∥ BC.(1)求 的值 ;
(2)证明△ADE与△ABC 相似.知3-练2 如果两个相似多边形的一组对应边长分别为3 cm
和2 cm,那么它们的相似比是( )
A. B. C. D.知3-练1.相似多边形的定义可作为判断两个多边形是否相似的
判定,即在多边形中,只有“边数相同”“角分别相等”
“边成比例”这三个条件同时成立时,才能说明这两个
多边形是相似多边形.
2.相似比的值与两个多边形的前后顺序有关.
3.相似比为1的两个相似多边形是全等多边形.
相似多边形的性质
相似比2课时流程逐点
导讲练课堂小结作业提升 你看上边的图形有何特点呢?今天我们就来研究
这个问题!1知识点相似多边形问 题知1-导 图中的两个大小不同的四边形
ABCD和四边形A1B1C1D1中,∠A=
∠A1,∠B=∠B1,∠C=∠C1,∠D
=∠D1, ,因此四边形ABCD与四边
形A1B1C1D1相似.知1-导定义:如果两个多边形的角分别相等,边成比例,那
么这两个多边形叫做相似多边形.
判定相似多边形的条件:
(1)所有的角分别相等;
(2)所有的边成比例.
以上的角分别相等,边成比例这两个条件是判定相
似多边形必备的条件,缺一不可.例1 如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,
GF⊥AB,垂足分别为点E,F.
求证:四边形AFGE与四边形ABCD相似.知1-讲导引:要判定两个多边形相似,从边和角两个方面
证明,即需证对应角相等,对应边的比相等.
证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠DAC
=∠BAC=45°.又∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG.
∴AE=EG=FG=AF,∴四边形AFGE为正方形.
∴ ,且∠EAF=∠DAB,
∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE与四边形ABCD相似.知1-讲 判断两个多边形是否相似,既要看它们的角是否
分别相等,也要看边是否成比例,两者缺一不可.例
如:两个矩形不一定相似,两个菱形也不一定相似,
两个正方形一定相似.1 如图所示的两个三角形相似吗?为什么?
2 任意两个矩形相似吗?为什么? 知1-练甲:将边长为3,4,5的三角形按图①的方式向
外扩张,得到新三角形,它们的对应边间距均
为1,则新三角形与原三角形相似.
乙:将邻边长为3和5的矩形按图②的方式向外
扩张,得到新矩形,它们的对应边间距均为1,
则新矩形与原矩形不相似.3 (中考·河北)在研究相似问题时,甲、乙同学的观点
如下:
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.甲对,乙不对 D.甲不对,乙对知1-练4 放大镜中的多边形与原多边形的关系是( )
A.形状不同,大小不同
B.形状相同,大小相同
C.形状相同,大小不同
D.形状不同,大小相同知1-练2知识点相似多边形的性质知2-导 如图的左边格点图中有一
个四边形,请在右边的格点图
中画出一个与该四边形相似的
图形.问 题 1 对于图中两个相似的四边形,它们的对应角,对应
边的比是否相等.问 题 2知识点知2-讲 图中的两个大小不同的四边形
ABCD和四边形A1B1C1D1中,
∠A=∠A1,∠B=∠B1,∠C=
∠C1,∠D=∠D1, ,因此四边形
ABCD与四边形A1B1C1D1相似.
由相似多边形的定义可知,相似多边形的对应角相
等,对应边成比例.知2-讲相似多边形的性质:相似多边形的对应边的比相等,
对应角相等.
作用:常用来求相似多边形中未知的边的长度和角的
度数.知2-讲例2 如图,四边形ABCD和EFGH相似,求角α,β的大
小和EF的长度x.解:因为四边形ABCD和EFGH相
似,所以它们的对应角相等,
由此可得α=∠C=83°, ∠A=∠E=118°.
在四边形ABCD中,
β=360°-(78°+83°+118°) = 81°.
因为四边形ABCD和EFGH相似,所以它们的对应边
成比例,由此可得
解得x=28. 知2-讲 利用相似多边形的性质求边长或角度,关键扣住
“对应”二字,找准对应边和对应角是解决问题的关
键.需要注意的是对应边是比相等,而对应角是直接
相等.1 如图所示的两个五边形相似,求a,b,c,
d的值.知2-练知2-练2 如图所示的两个四边形相似,则α的度数是( )
A.87° B.60° C.75° D.120°
3 一个多边形的边长分别为2,3,4,5,6,另一个多
边形和这个多边形相似,且最短边长为6,则最长边
长为( )
A.18 B.12 C.24 D.30知3-导3知识点相似比 两个图形相似,其中一个图形可以看作
由另一个图形放大或缩小得到.例如,放映电
影时,投在屏幕上的画面就是胶片上图形的
放大;用复印机把一个图形放大或缩小后所
得的图形,都与原来的图形相似.图中有2对图
形,每对图形中的两个图形相似.其中较大(小)的图形可以看成是
由较小(大)的图形放大(缩小)得到的.
上边的图形是相似图形,它们对应的比值有何关系呢?我
们用尺子测量一下,看看.通过测量,我们发现每两个图形对
应边的比值相等,我们把相似多边形对应边的比称为相似比.知3-导相似比的定义:相似多边形对应边的比称为相似比.
要点精析:
(1)相似比与两个多边形的前后顺序有关;
(2)相似比为1的两个相似多边形为全等多边形.知3-讲导引:相似多边形的对应边的比相等,其比值就是相似比.
解:(1)设AD=x,则DM= .∵矩形DMNC与矩形ABCD相似,
∴x2=32.
∴x=4 或x=-4 (舍去),即AD的长为4 .
(2)矩形DMNC与矩形ABCD的相似比为例3 如图,把矩形ABCD对折,折痕为MN,矩形DMNC与
矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.知3-讲 利用相似多边形的性质求线段长及相似比的方法:
先找出与已知边、未知边相关的四条对应线段,再通过
设未知数并用含未知数的式子表示其中的部分线段,最
后通过相似多边形的对应边成比例建立方程进行计算.
这种巧用方程思想的方法在相似多边形的计算中经常
运用.1 如图,DE ∥ BC.(1)求 的值 ;
(2)证明△ADE与△ABC 相似.知3-练2 如果两个相似多边形的一组对应边长分别为3 cm
和2 cm,那么它们的相似比是( )
A. B. C. D.知3-练1.相似多边形的定义可作为判断两个多边形是否相似的
判定,即在多边形中,只有“边数相同”“角分别相等”
“边成比例”这三个条件同时成立时,才能说明这两个
多边形是相似多边形.
2.相似比的值与两个多边形的前后顺序有关.
3.相似比为1的两个相似多边形是全等多边形.
