27.2.1 相似三角形及平行线分线段成比例课件
文档属性
| 名称 | 27.2.1 相似三角形及平行线分线段成比例课件 |  | |
| 格式 | zip | ||
| 文件大小 | 710.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 08:10:24 | ||
图片预览










文档简介
课件33张PPT。第二十七章 相似27.2 相似三角形第1课时 相似三角形及平行线
分线段成比例1课堂讲解相似三角形
平行线分线段成比例的基本事实
平行线分线段成比例基本事实的推论2课时流程逐点
导讲练课堂小结作业提升提问:
(1)什么是成比例线段?
(2)什么是相似多边形?
(3)你能不通过测量快速将一根绳子分成两部分,
使得这两部分的比是2 ∶ 3吗?
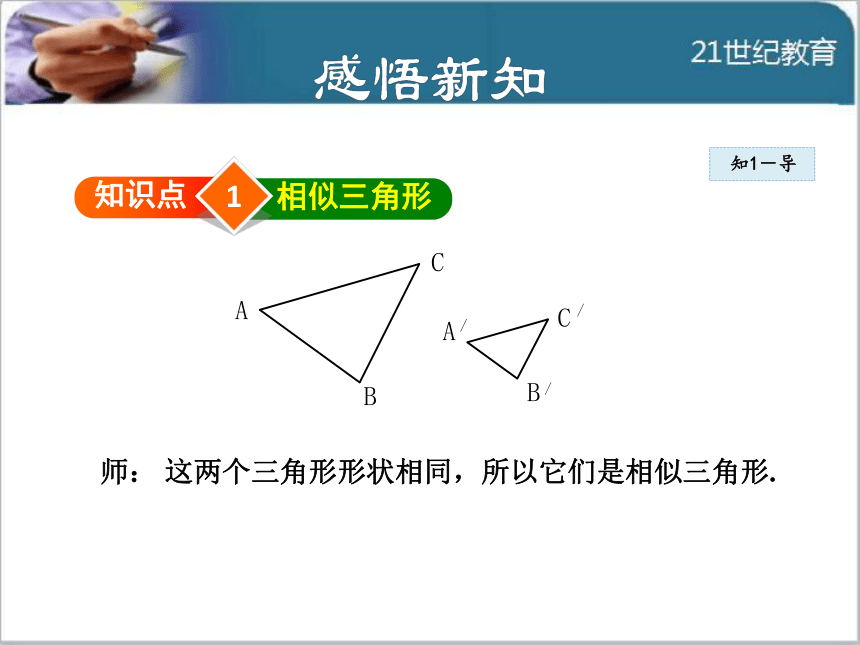
1知识点相似三角形知1-导师: 这两个三角形形状相同,所以它们是相似三角形.知1-导在相似多边形中,最简单的就是相似三角形(similar
triangles).如图,在△ABC和△A′B′C′中,如果
∠A=∠A′,∠B=∠B′,∠C=∠C′,
即三个角分别相等,三条边成比例,我们就说△ABC与△A′B′C′
相似,相似比为k.相似用符号“∽”表示,读作“相似于”.
△ABC与△A′B′C′相似记作 “△ABC∽△A′B′C′”.定义:如果两个三角形中,三个角分别相等,三条
边成比例,那么这两个三角形相似.
数学表达式:如图,在△ABC和△A′B′C′中,
△ABC∽△A′B′C′.
(注:?为等价符号)知1-讲要点精析:
(1)判定两个三角形相似的必备条件:三个角分别相
等,三条边成比例;
(2)两三角形相似又为解题提供了条件;
(3)相似三角形具有传递性:即若△ABC∽△A′B′C′,
△A′B′C′∽△A″B″C″,则△ABC∽△A″B″C″;
(4)相似比为1的两个相似三角形全等,反过来两个全
等三角形可以看作是相似比是1的相似三角形.知1-讲例1 如图所示,△ABC∽△DEF,其中AB=6,DE=9,
指出对应边、对应角,
并求出相似比.
导引:用“∽”表示两个图形相似时,表示对应顶点的
字母应该写在对应的位置上.
解:对应边分别是:AB与DE,BC与EF,AC与DF.
对应角分别是:∠A与∠D,∠B与∠E,∠C与∠F.
∵AB∶DE=6∶9=2∶3,∴相似比为2∶3.
知1-讲知1-讲(1)对应性:表示两三角形相似时,要注意对应性,
即要把对应顶点写在对应位置上.
(2)顺序性:求两相似三角形的相似比,要注意顺序
性.若当△ABC∽△A′B′C′时,
则△A′B′C′∽△ABC时,
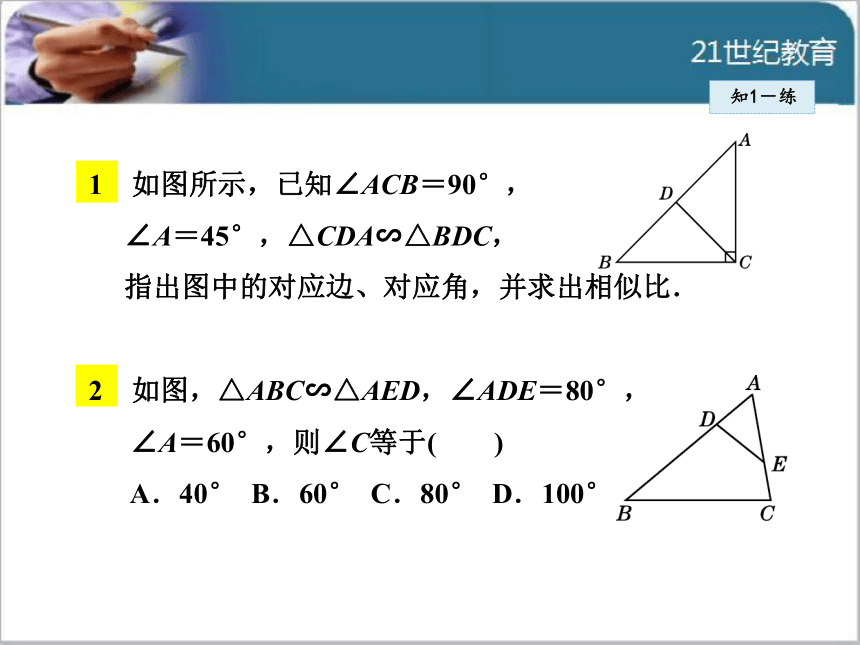
如图所示,已知∠ACB=90°,
∠A=45°,△CDA∽△BDC,
指出图中的对应边、对应角,并求出相似比.
如图,△ABC∽△AED,∠ADE=80°,
∠A=60°,则∠C等于( )
A.40° B.60° C.80° D.100°
知1-练例2 如图,在△ABC中,DE∥BC.
(1)求 的值;
(2)△ADE与△ABC相似吗?
为什么?
导引:(1)直接利用线段的长度求它们的比值;
(2)抓住两个条件判断:①三条边成比例;
②三个角分别相等.
知1-讲解:(1)由图形可知AB=9,AC=6.
(2)△ADE与△ABC相似.理由如下:
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB.
由(1)知
又∵∠DAE=∠BAC,
∴△ADE∽△ABC.
知1-讲知1-讲由于三角形是最简单的多边形,因此判定两个
三角形相似可以根据判定两个多边形相似的方法,
即利用相似三角形的定义证出三个角分别相等,三
条边成比例即可.判断下列两组三角形是否相似,请说明理由.
(1)△ABC和△A′B′C′都是等边三角形;
(2)在△ABC中,∠C=90°,AC=BC;
在△A′B′C′中,∠C′=90°,A′C′=B′C′.
如图,△ABC∽△DEF,相似比为1∶2.若BC=1,则EF的长是( )
A.1 B.2
C.3 D.4
知1-练2知识点平行线分线段成比例的基本事实知2-导如图,任意画两条直线l1,l2,再画三条与l1,l2都相交的平行线l3, l4,l5.分别度量l3, l4,l5在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度, 相等吗?
任意平移l5, 还相等吗?探究知2-讲如图,小方格的边长都是1,直线a∥b∥ c ,分别
交直线m,n于 A1,A2,A3,B1,B2,B3 . 知2-讲计算 可以发现:
所以
于是有,平行线分线段成比例定理
两条直线被一组平行线所截,所得的对应线段成比
例.知2-讲平行线分线段成比例的基本事实:两条直线被一组平
行线所截,所得的对应线段成比例.
数学表达式:如图,∵l3∥l4∥l5,
可简记为:知2-讲(1)一组平行线两两平行,被截直线不一定平行;
(2)所有的成比例线段是指被截直线上的线段,与这组
平行线上的线段无关;
(3)当上比下的值为1时,说明这组平行线间的距离相
等.知2-讲例3 如图,已知AB∥CD∥EF,AF交BE于点H,下列结论中错误的是( )
A. B.
C. D.
导引:本题中利用平行线分线段成比例的基本事实
的图形主要有“A”型和“X”型,从每种图形
中找出比例线段即可判断.C知2-讲解析:根据AB∥CD∥EF,结合平行线分线段成比
例的基本事实可得解.
∵AB∥CD∥EF,
故选项A,B,D正确.
∵CD∥EF,∴ 故选项C错误.知2-讲在题目中如遇到与直线平行相关的问题时,可
从两个方面得到信息:一是位置角之间的关系(同位
角相等、内错角相等、同旁内角互补);二是线段之
间的关系,即平行线分线段成比例.如图,直线l1∥l2∥l3,若AB=2,BC=3,
DE=1,则EF的值为( )
A. B. C.6 D.
(2015·舟山)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,
BC=5,则 的值为( )
A. B.2 C. D.知2-练知3-导3知识点平行线分线段成比例基本事实的推论把平行线分线段成比例的基本事实应用到三角形中,会出
现下面两种情况.
在图 (1)中,把l4看成平行于△ABC的边BC的直线;在图 (2)
中,把l3看成平行于△ABC的边BC的直线,那么我们可以得到结
论.知3-导平行于三角形一边的直线截其他两边(或两边
的延长线),所得的对应线段成比例.
数学表达式:
如图,∵DE∥BC,知3-导(1)本推论实质是平行线分线段成比例的基本事实中
一组平行线中的一条过三角形一顶点,一条在三
角形一边上的一种特殊情况.
(2)成比例线段不涉及平行线所在的边上的线段. 例4 如图,F是 ABCD的边CD上一点,连接BF,并延长BF交AD的延长线于点E.求证:
解析: 先根据平行四边形的性质得出AD∥BC,AB∥
CD,再根据平行线分线段成比例定理的推论得
出对应边成比例即可得出结论.
知3-讲证明:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC.
(平行于三角形一边的直线截其他两
边,所得的对应线段成比例).
同理可得
知3-讲知3-讲本题是证明等积式的典型题.要证明 经
常要把它转化为两个等式: 我们通常
把 叫做中间比.而找中间比的常见的方法就是通过
找到平行线,然后利用平行线分线段成比例定理和它
的推论来构造比例式.1 如图,已知AB∥EF∥CD,若AB=6 cm,CD=9 cm,BF=7 cm.则BC=________.知3-练2 如图,已知AB∥CD,AC与BD交于点O,则下列比例式中不成立的是( )
A.OC∶OD=OA∶OB
B.OC∶OD=OB∶OA
C.OC∶AC=OD∶DB
D.BD∶AC=OB∶OA知3-练3 如图,在平行四边形ABCD中,AC与BD交于点O,E为OD的中点,连接AE并延长交DC于点F,则EF∶AE等于( )
A.1∶4 B.1 ∶ 3 C.2 ∶ 3 D.1 ∶ 2知3-练平行线除了具备造成“三线八角”相等或互补的
功能外,还可以分线段成比例,而利用平行线得线
段成比例的基本思路是:
(1)善于从较复杂的几何图形中分离出基本图形:
“ 型”或“ 型”,得到相应的比例式;
(2)平行是前提条件,没有平行线可以添加辅助线,
一般从分点或中点出发作平行线.
分线段成比例1课堂讲解相似三角形
平行线分线段成比例的基本事实
平行线分线段成比例基本事实的推论2课时流程逐点
导讲练课堂小结作业提升提问:
(1)什么是成比例线段?
(2)什么是相似多边形?
(3)你能不通过测量快速将一根绳子分成两部分,
使得这两部分的比是2 ∶ 3吗?
1知识点相似三角形知1-导师: 这两个三角形形状相同,所以它们是相似三角形.知1-导在相似多边形中,最简单的就是相似三角形(similar
triangles).如图,在△ABC和△A′B′C′中,如果
∠A=∠A′,∠B=∠B′,∠C=∠C′,
即三个角分别相等,三条边成比例,我们就说△ABC与△A′B′C′
相似,相似比为k.相似用符号“∽”表示,读作“相似于”.
△ABC与△A′B′C′相似记作 “△ABC∽△A′B′C′”.定义:如果两个三角形中,三个角分别相等,三条
边成比例,那么这两个三角形相似.
数学表达式:如图,在△ABC和△A′B′C′中,
△ABC∽△A′B′C′.
(注:?为等价符号)知1-讲要点精析:
(1)判定两个三角形相似的必备条件:三个角分别相
等,三条边成比例;
(2)两三角形相似又为解题提供了条件;
(3)相似三角形具有传递性:即若△ABC∽△A′B′C′,
△A′B′C′∽△A″B″C″,则△ABC∽△A″B″C″;
(4)相似比为1的两个相似三角形全等,反过来两个全
等三角形可以看作是相似比是1的相似三角形.知1-讲例1 如图所示,△ABC∽△DEF,其中AB=6,DE=9,
指出对应边、对应角,
并求出相似比.
导引:用“∽”表示两个图形相似时,表示对应顶点的
字母应该写在对应的位置上.
解:对应边分别是:AB与DE,BC与EF,AC与DF.
对应角分别是:∠A与∠D,∠B与∠E,∠C与∠F.
∵AB∶DE=6∶9=2∶3,∴相似比为2∶3.
知1-讲知1-讲(1)对应性:表示两三角形相似时,要注意对应性,
即要把对应顶点写在对应位置上.
(2)顺序性:求两相似三角形的相似比,要注意顺序
性.若当△ABC∽△A′B′C′时,
则△A′B′C′∽△ABC时,
如图所示,已知∠ACB=90°,
∠A=45°,△CDA∽△BDC,
指出图中的对应边、对应角,并求出相似比.
如图,△ABC∽△AED,∠ADE=80°,
∠A=60°,则∠C等于( )
A.40° B.60° C.80° D.100°
知1-练例2 如图,在△ABC中,DE∥BC.
(1)求 的值;
(2)△ADE与△ABC相似吗?
为什么?
导引:(1)直接利用线段的长度求它们的比值;
(2)抓住两个条件判断:①三条边成比例;
②三个角分别相等.
知1-讲解:(1)由图形可知AB=9,AC=6.
(2)△ADE与△ABC相似.理由如下:
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB.
由(1)知
又∵∠DAE=∠BAC,
∴△ADE∽△ABC.
知1-讲知1-讲由于三角形是最简单的多边形,因此判定两个
三角形相似可以根据判定两个多边形相似的方法,
即利用相似三角形的定义证出三个角分别相等,三
条边成比例即可.判断下列两组三角形是否相似,请说明理由.
(1)△ABC和△A′B′C′都是等边三角形;
(2)在△ABC中,∠C=90°,AC=BC;
在△A′B′C′中,∠C′=90°,A′C′=B′C′.
如图,△ABC∽△DEF,相似比为1∶2.若BC=1,则EF的长是( )
A.1 B.2
C.3 D.4
知1-练2知识点平行线分线段成比例的基本事实知2-导如图,任意画两条直线l1,l2,再画三条与l1,l2都相交的平行线l3, l4,l5.分别度量l3, l4,l5在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度, 相等吗?
任意平移l5, 还相等吗?探究知2-讲如图,小方格的边长都是1,直线a∥b∥ c ,分别
交直线m,n于 A1,A2,A3,B1,B2,B3 . 知2-讲计算 可以发现:
所以
于是有,平行线分线段成比例定理
两条直线被一组平行线所截,所得的对应线段成比
例.知2-讲平行线分线段成比例的基本事实:两条直线被一组平
行线所截,所得的对应线段成比例.
数学表达式:如图,∵l3∥l4∥l5,
可简记为:知2-讲(1)一组平行线两两平行,被截直线不一定平行;
(2)所有的成比例线段是指被截直线上的线段,与这组
平行线上的线段无关;
(3)当上比下的值为1时,说明这组平行线间的距离相
等.知2-讲例3 如图,已知AB∥CD∥EF,AF交BE于点H,下列结论中错误的是( )
A. B.
C. D.
导引:本题中利用平行线分线段成比例的基本事实
的图形主要有“A”型和“X”型,从每种图形
中找出比例线段即可判断.C知2-讲解析:根据AB∥CD∥EF,结合平行线分线段成比
例的基本事实可得解.
∵AB∥CD∥EF,
故选项A,B,D正确.
∵CD∥EF,∴ 故选项C错误.知2-讲在题目中如遇到与直线平行相关的问题时,可
从两个方面得到信息:一是位置角之间的关系(同位
角相等、内错角相等、同旁内角互补);二是线段之
间的关系,即平行线分线段成比例.如图,直线l1∥l2∥l3,若AB=2,BC=3,
DE=1,则EF的值为( )
A. B. C.6 D.
(2015·舟山)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,
BC=5,则 的值为( )
A. B.2 C. D.知2-练知3-导3知识点平行线分线段成比例基本事实的推论把平行线分线段成比例的基本事实应用到三角形中,会出
现下面两种情况.
在图 (1)中,把l4看成平行于△ABC的边BC的直线;在图 (2)
中,把l3看成平行于△ABC的边BC的直线,那么我们可以得到结
论.知3-导平行于三角形一边的直线截其他两边(或两边
的延长线),所得的对应线段成比例.
数学表达式:
如图,∵DE∥BC,知3-导(1)本推论实质是平行线分线段成比例的基本事实中
一组平行线中的一条过三角形一顶点,一条在三
角形一边上的一种特殊情况.
(2)成比例线段不涉及平行线所在的边上的线段. 例4 如图,F是 ABCD的边CD上一点,连接BF,并延长BF交AD的延长线于点E.求证:
解析: 先根据平行四边形的性质得出AD∥BC,AB∥
CD,再根据平行线分线段成比例定理的推论得
出对应边成比例即可得出结论.
知3-讲证明:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC.
(平行于三角形一边的直线截其他两
边,所得的对应线段成比例).
同理可得
知3-讲知3-讲本题是证明等积式的典型题.要证明 经
常要把它转化为两个等式: 我们通常
把 叫做中间比.而找中间比的常见的方法就是通过
找到平行线,然后利用平行线分线段成比例定理和它
的推论来构造比例式.1 如图,已知AB∥EF∥CD,若AB=6 cm,CD=9 cm,BF=7 cm.则BC=________.知3-练2 如图,已知AB∥CD,AC与BD交于点O,则下列比例式中不成立的是( )
A.OC∶OD=OA∶OB
B.OC∶OD=OB∶OA
C.OC∶AC=OD∶DB
D.BD∶AC=OB∶OA知3-练3 如图,在平行四边形ABCD中,AC与BD交于点O,E为OD的中点,连接AE并延长交DC于点F,则EF∶AE等于( )
A.1∶4 B.1 ∶ 3 C.2 ∶ 3 D.1 ∶ 2知3-练平行线除了具备造成“三线八角”相等或互补的
功能外,还可以分线段成比例,而利用平行线得线
段成比例的基本思路是:
(1)善于从较复杂的几何图形中分离出基本图形:
“ 型”或“ 型”,得到相应的比例式;
(2)平行是前提条件,没有平行线可以添加辅助线,
一般从分点或中点出发作平行线.
