27.2.2 平行线分线段成比例的应用课件
文档属性
| 名称 | 27.2.2 平行线分线段成比例的应用课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 133.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 08:12:12 | ||
图片预览




文档简介
课件11张PPT。第二十七章 相似27.2 相似三角形第2课时 平行线分线段成比
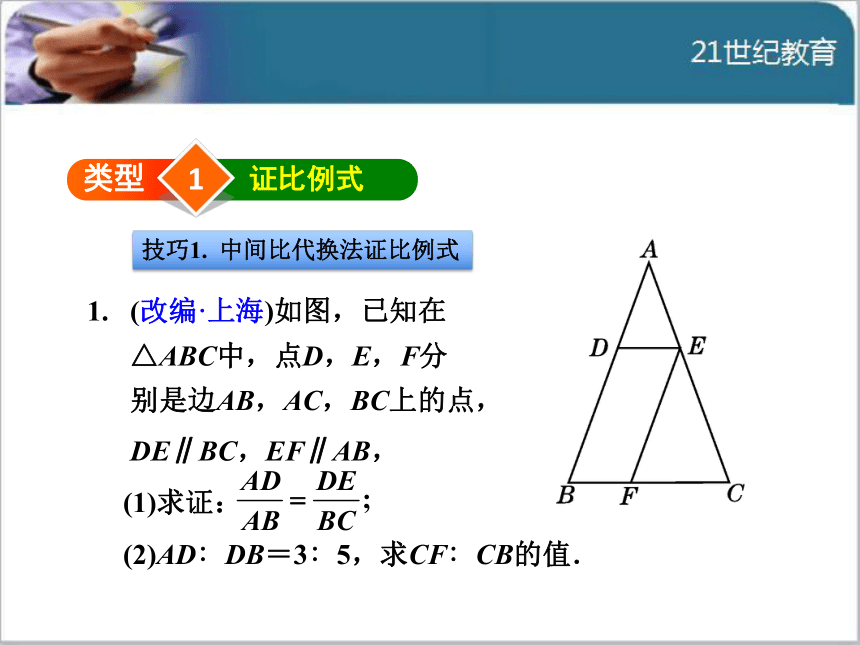
例的应用1类型 证比例式技巧1. 中间比代换法证比例式(改编·上海)如图,已知在
△ABC中,点D,E,F分
别是边AB,AC,BC上的点,
DE∥BC,EF∥AB,
(1)求证:
(2)AD∶DB=3∶5,求CF∶CB的值.∵DE∥BC,EF∥AB,
∴四边形DEFB为平行四边形.∴DE=BF.
∵DE∥BC, ∴
∵EF∥AB,∴
又∵DE=BF, ∴
∴(1)证明:∵AD∶DB=3∶5,
∴BD∶AB=5∶8.
∵DE∥BC,
∴CE∶AC=BD∶AB=5∶8.
∵EF∥AB,
∴CF∶CB=CE∶AC=5∶8.(2)解:技巧2.等积代换法证比例式如图,在△ABC中,D是AB上一点,E是△ABC内一点,DE∥BC,过D作AC的平行线交CE的延长线于F,CF与AB交于P,连接BF,求证:
证明:∵DE∥BC,∴
∴PD·PC=PE·PB.
∵DF∥AC,∴
∴PD·PC=PF·PA.
∴PE·PB=PF·PA. ∴证明:∵EF∥CD,
∴
∵DE∥BC. ∴
∴技巧3. 等比代换法证比例中项如图,在△ABC中,DE∥BC,EF∥CD.
求证:2类型证线段相等技巧4. 等比例后项证线段相等(等比例过渡法)如图,在△ABC中,∠ACB=90°,∠B>∠A,
点D为边AB的中点,DE∥BC交AC于点E,
CF∥BA交DE的延长线于点F.
求证:DE=EF.证明:∵DE∥BC,∴
∵点D为AB的中点,
∴AD=DB,即
∵CF∥BA,
∴
∴DE=EF.3类型证比例和为1技巧5. 同分母的中间比代换法5. 如图,已知AC∥FE∥BD,求证:∵AC∥EF,
∴ ①.
又∵FE∥BD,
∴ ② .
①+②,得
即证明:
例的应用1类型 证比例式技巧1. 中间比代换法证比例式(改编·上海)如图,已知在
△ABC中,点D,E,F分
别是边AB,AC,BC上的点,
DE∥BC,EF∥AB,
(1)求证:
(2)AD∶DB=3∶5,求CF∶CB的值.∵DE∥BC,EF∥AB,
∴四边形DEFB为平行四边形.∴DE=BF.
∵DE∥BC, ∴
∵EF∥AB,∴
又∵DE=BF, ∴
∴(1)证明:∵AD∶DB=3∶5,
∴BD∶AB=5∶8.
∵DE∥BC,
∴CE∶AC=BD∶AB=5∶8.
∵EF∥AB,
∴CF∶CB=CE∶AC=5∶8.(2)解:技巧2.等积代换法证比例式如图,在△ABC中,D是AB上一点,E是△ABC内一点,DE∥BC,过D作AC的平行线交CE的延长线于F,CF与AB交于P,连接BF,求证:
证明:∵DE∥BC,∴
∴PD·PC=PE·PB.
∵DF∥AC,∴
∴PD·PC=PF·PA.
∴PE·PB=PF·PA. ∴证明:∵EF∥CD,
∴
∵DE∥BC. ∴
∴技巧3. 等比代换法证比例中项如图,在△ABC中,DE∥BC,EF∥CD.
求证:2类型证线段相等技巧4. 等比例后项证线段相等(等比例过渡法)如图,在△ABC中,∠ACB=90°,∠B>∠A,
点D为边AB的中点,DE∥BC交AC于点E,
CF∥BA交DE的延长线于点F.
求证:DE=EF.证明:∵DE∥BC,∴
∵点D为AB的中点,
∴AD=DB,即
∵CF∥BA,
∴
∴DE=EF.3类型证比例和为1技巧5. 同分母的中间比代换法5. 如图,已知AC∥FE∥BD,求证:∵AC∥EF,
∴ ①.
又∵FE∥BD,
∴ ② .
①+②,得
即证明:
