27.2.3 用平行线判定三角形相似课件
文档属性
| 名称 | 27.2.3 用平行线判定三角形相似课件 |  | |
| 格式 | zip | ||
| 文件大小 | 422.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 08:13:45 | ||
图片预览








文档简介
课件20张PPT。第二十七章 相似27.2 相似三角形第3课时 用平行线判定
三角形相似1课堂讲解平行线判定三角形相似定理
平行线判定三角形相似定理的应用2课时流程逐点
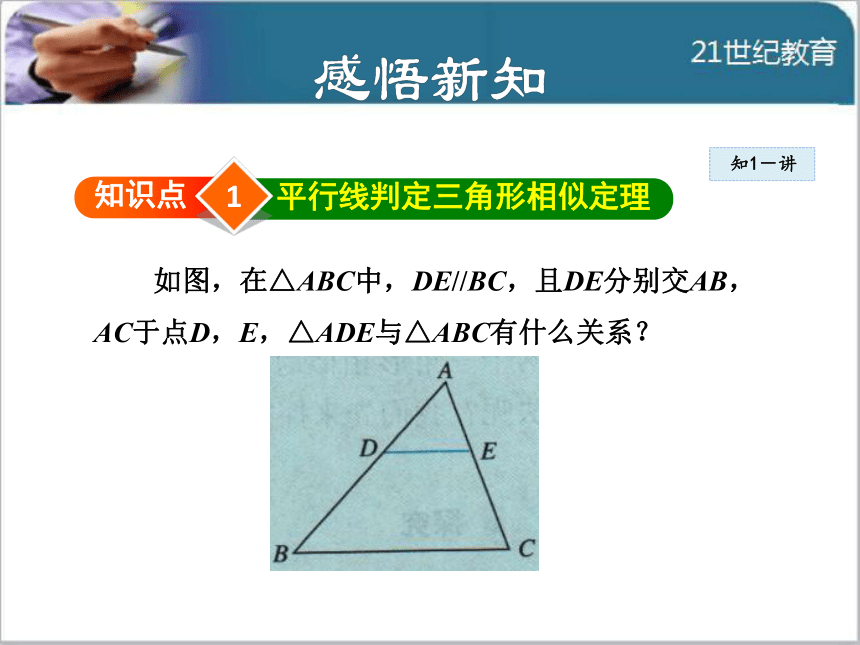
导讲练课堂小结作业提升判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?1知识点平行线判定三角形相似定理知1-讲如图,在△ABC中,DE//BC,且DE分别交AB,AC于点D,E,△ADE与△ABC有什么关系??知1-讲解析:直觉告诉我们,△ADE与△ABC相似,我们通过相似
的定义证明它,即证明∠A=∠A, ∠ADE=∠B,
∠AED=∠C, 由前面的结论可得,
而 中的DE不在△ABC的边BC上,不
能直接利用前面的结论.但从要证的 可以看
出,除DE外,AE,AC,BC都在△ABC的边上,因
此只需将DE平移到BC边上去,使得BF=DE,再证明
就可以了(如图).只要过点E作EF//AB,交
BC于点F,BF就是平移DE所得的线段. 知1-讲先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠A=∠A.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E作EF//AB,交BC于点F.
∵DE//BC,EF//AB,
知1-讲∵四边形DBFE是平行四边形,
∴DE=BF.
这样,我们证明了△ADE和△ABC的角分别相等,
边成比例,所以 △ADE∽△ABC.因此,我们有如下判定
三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似.例1 如图,在?ABCD中,F是AD边上的任意一点,连接BF并延长交CD的延长线于点E,则图中与△DEF相似的三角形共有( )
A.1个 B.2个
C.3个 D.4个
导引:由于四边形ABCD是平行四边形,因此FD∥BC,
DE∥AB.于是可从图中找出符合“A”型相似的
△DEF与△CEB,符合“X”型相似的△DEF与
△ABF.故选B.知1-讲B利用平行线寻找相似三角形的方法:
在线段较多的图形中寻找相似三角形,如果图中有
线段平行的条件,则集中精力在图形中寻找符合“A”
型或“X”型的基本图形,这不但是解本题的首要之选,
也是今后解本类题目的首要之选.知1-讲知1-讲用平行线判定三角形相似的定理:平行于三角形一
边的直线和其他两边相交,所构成的三角形与原三
角形相似.
数学表达式:如图,
∵DE∥BC,
∴△ABC∽△ADE.知1-讲要点精析:
(1)定理中“和其他两边相交”是指和其他两边所在
直线相交.
(2)根据定理得到的相似三角形的三个基本图形中都
有BC∥DE,图 (1)(2)很像大写字母A,故我们称
之为“A”型相似;图 (3)很像大写字母X,故我们
称之为“X”型相似(也像阿拉伯数字“8”).如图,在△ABC中,DE∥BC,且AD=3,DB=2.写出图中的相似三角形,并指出其相似比.知1-练如图,在△ABC中,EF∥BC,DG∥AB,EF和DG相交于点H,则图中与△ABC相似的
三角形共有( )
A.1个 B.2个 C.3个 D.0个
(2016?盐城)如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E.
在不添加辅助线的情况下,与
△AEF相似的三角形有( )
A.0个 B.1个 C.2个 D.3个知1-练2知识点平行线判定三角形相似定理的应用知2-导如图所示,要测量一个池塘的长是多少,不能直接测量距离,小明做了△ABC,取
池塘的两个点D,E,使DE∥BC,
测出BC,AD,AB的长就可以算出
DE的长,你知道为什么吗?
原来由DE∥BC可以得到△ABC∽△ADE,所以
AD∶AB=DE∶BC.知2-导通过建立相似三角形数学模型可以解决实际
问题.知2-讲例2 如图,在?ABCD中,AE=EB,AF=2,则FC等于________.
导引:有平行四边形,就提供了平行线,就有三角形相似,
就有对应边的比相等,就能求出FC的长.
在?ABCD中,∵AB∥CD,AB=CD,
∴△AEF∽△CDF.
∵AE=EB,∴AE= AB= CD.
∴CF=2AF=4.4知2-讲利用证三角形相似求线段的长的方法:当三角
形被平行线所截形成“A”型或“X”型的图形,并
且所求的线段或已知线段在平行的边上,通常考虑通
过证三角形相似,再利用相似三角形的对应边的比相
等构建包含已知与未知线段的比例式,即可求出线段
的长.〈株洲〉如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A. B. C. D.知2-练(2015?毕节)如图,在△ABC中,DE∥BC,AE∶EC=
2∶3,DE=4,则BC等于( )
A.10 B.8
C.9 D.6
3 如图,AB∥CD,AD与BC相交于点O,那么在下列比例式中,正确的是( )
A. B.
C. D.知2-练利用平行线证比例式或等积式的方法:当比例
式或等积式中的线段不在平行线上时,可直接利用
平行线分线段成比例的基本事实证明;当比例式或
等积式中的线段有的在平行线上时,可直接利用平
行线截三角形相似的对应边成比例证明;当比例式
或等积式中的线段不是对应线段时,利用转化思想,
用等线段、等比例、等积替换进行论证.
三角形相似1课堂讲解平行线判定三角形相似定理
平行线判定三角形相似定理的应用2课时流程逐点
导讲练课堂小结作业提升判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?1知识点平行线判定三角形相似定理知1-讲如图,在△ABC中,DE//BC,且DE分别交AB,AC于点D,E,△ADE与△ABC有什么关系??知1-讲解析:直觉告诉我们,△ADE与△ABC相似,我们通过相似
的定义证明它,即证明∠A=∠A, ∠ADE=∠B,
∠AED=∠C, 由前面的结论可得,
而 中的DE不在△ABC的边BC上,不
能直接利用前面的结论.但从要证的 可以看
出,除DE外,AE,AC,BC都在△ABC的边上,因
此只需将DE平移到BC边上去,使得BF=DE,再证明
就可以了(如图).只要过点E作EF//AB,交
BC于点F,BF就是平移DE所得的线段. 知1-讲先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠A=∠A.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E作EF//AB,交BC于点F.
∵DE//BC,EF//AB,
知1-讲∵四边形DBFE是平行四边形,
∴DE=BF.
这样,我们证明了△ADE和△ABC的角分别相等,
边成比例,所以 △ADE∽△ABC.因此,我们有如下判定
三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似.例1 如图,在?ABCD中,F是AD边上的任意一点,连接BF并延长交CD的延长线于点E,则图中与△DEF相似的三角形共有( )
A.1个 B.2个
C.3个 D.4个
导引:由于四边形ABCD是平行四边形,因此FD∥BC,
DE∥AB.于是可从图中找出符合“A”型相似的
△DEF与△CEB,符合“X”型相似的△DEF与
△ABF.故选B.知1-讲B利用平行线寻找相似三角形的方法:
在线段较多的图形中寻找相似三角形,如果图中有
线段平行的条件,则集中精力在图形中寻找符合“A”
型或“X”型的基本图形,这不但是解本题的首要之选,
也是今后解本类题目的首要之选.知1-讲知1-讲用平行线判定三角形相似的定理:平行于三角形一
边的直线和其他两边相交,所构成的三角形与原三
角形相似.
数学表达式:如图,
∵DE∥BC,
∴△ABC∽△ADE.知1-讲要点精析:
(1)定理中“和其他两边相交”是指和其他两边所在
直线相交.
(2)根据定理得到的相似三角形的三个基本图形中都
有BC∥DE,图 (1)(2)很像大写字母A,故我们称
之为“A”型相似;图 (3)很像大写字母X,故我们
称之为“X”型相似(也像阿拉伯数字“8”).如图,在△ABC中,DE∥BC,且AD=3,DB=2.写出图中的相似三角形,并指出其相似比.知1-练如图,在△ABC中,EF∥BC,DG∥AB,EF和DG相交于点H,则图中与△ABC相似的
三角形共有( )
A.1个 B.2个 C.3个 D.0个
(2016?盐城)如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E.
在不添加辅助线的情况下,与
△AEF相似的三角形有( )
A.0个 B.1个 C.2个 D.3个知1-练2知识点平行线判定三角形相似定理的应用知2-导如图所示,要测量一个池塘的长是多少,不能直接测量距离,小明做了△ABC,取
池塘的两个点D,E,使DE∥BC,
测出BC,AD,AB的长就可以算出
DE的长,你知道为什么吗?
原来由DE∥BC可以得到△ABC∽△ADE,所以
AD∶AB=DE∶BC.知2-导通过建立相似三角形数学模型可以解决实际
问题.知2-讲例2 如图,在?ABCD中,AE=EB,AF=2,则FC等于________.
导引:有平行四边形,就提供了平行线,就有三角形相似,
就有对应边的比相等,就能求出FC的长.
在?ABCD中,∵AB∥CD,AB=CD,
∴△AEF∽△CDF.
∵AE=EB,∴AE= AB= CD.
∴CF=2AF=4.4知2-讲利用证三角形相似求线段的长的方法:当三角
形被平行线所截形成“A”型或“X”型的图形,并
且所求的线段或已知线段在平行的边上,通常考虑通
过证三角形相似,再利用相似三角形的对应边的比相
等构建包含已知与未知线段的比例式,即可求出线段
的长.〈株洲〉如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A. B. C. D.知2-练(2015?毕节)如图,在△ABC中,DE∥BC,AE∶EC=
2∶3,DE=4,则BC等于( )
A.10 B.8
C.9 D.6
3 如图,AB∥CD,AD与BC相交于点O,那么在下列比例式中,正确的是( )
A. B.
C. D.知2-练利用平行线证比例式或等积式的方法:当比例
式或等积式中的线段不在平行线上时,可直接利用
平行线分线段成比例的基本事实证明;当比例式或
等积式中的线段有的在平行线上时,可直接利用平
行线截三角形相似的对应边成比例证明;当比例式
或等积式中的线段不是对应线段时,利用转化思想,
用等线段、等比例、等积替换进行论证.
