27.2.4 用三边比例关系判定三角形相似课件
文档属性
| 名称 | 27.2.4 用三边比例关系判定三角形相似课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 481.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 00:00:00 | ||
图片预览






文档简介
课件19张PPT。第二十七章 相似27.2 相似三角形第4课时 用三边比例关系判
定三角形相似1课堂讲解三边成比例的两个三角形相似
网格上相似三角形的判定2课时流程逐点
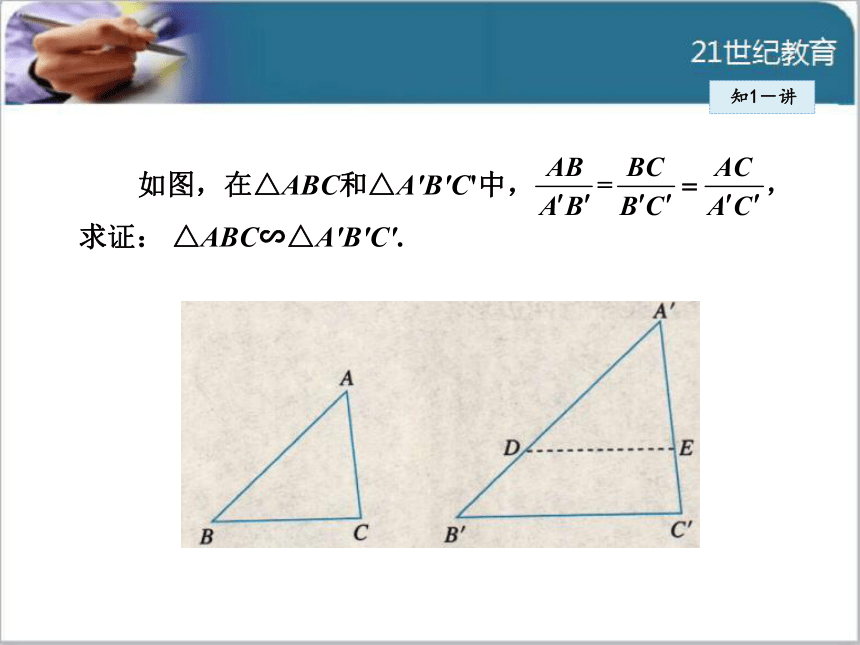
导讲练课堂小结作业提升判定两个三角形全等我们有SSS的方法,类似地,判定两个三角形相似是否也有类似的简单方法呢?1知识点三边成比例的两个三角形相似知1-讲任意画一个三角形,再画另一个三角形,使它的各边长都是原来各边长的2倍,度量这两个三角形的对应角,他们对应相等吗?这两个三角形全等吗??问 题知1-讲如图,在△ABC和△A′B′C′中,
则△ABC与
△A′B′C′相似吗?为什么?
分析:这时可在A′B′上截取A′D=AB,再过D作DE//
B′C′,由△A′DE∽△A′B′C′,再证明△ABC
≌△A′DE,则可得到△ABC∽△A′B′C′.思 考知1-讲如图,在△ABC和△A'B'C'中,
求证: △ABC∽△A'B'C'. 证明:在线段A′B′(或它的延长线)上截取A′D=AB,过点D
作 DE//B′C′,交A′C′于点E.根据前面的定理,可得
△A′DE∽△A'B'C'.
∴DE=BC,A′E=AC.
∴ △A′DE≌△ABC.
∴△ABC ∽△A'B'C'.知1-讲 △A′DE是证明的中介,它把△ABC与△A′B′C′联系起来.知1-讲由此我们得到利用三边判定三角形相似的定理
(如图):
三边成比例的两个三角形相似.△ABC ∽△A'B'C'例1 根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
AB=4 cm,BC=6 cm,AC=8 cm,
A′B′= 12 cm,B′C′= 18 cm,A′C′=24 cm.?
解:
∴△ABC ∽△A'B'C'.
知1-讲知1-讲这个判定三角形相似的方法与三角形全等的判
定方法“边边边”十分相似,所不同的是在相似的
判定方法中的 “三边”要求的是“比相等”. 三边
的对应关系是“短∶短”“中∶中”“长∶长”.已知:如图,AD是△ABC的高,E,F分别是AB,AC的中点.求证:△DEF∽△ABC.知1-练若△ABC和△A′B′C′满足下列条件,其中使△ABC与△A′B′C′相似的是( )
A.AB=2.5 cm,BC=2 cm,AC=3 cm;A′B′=3 cm,B′C′=4 cm,A′C′=6 cm
B.AB=2 cm,BC=3 cm,AC=4 cm;A′B′=3 cm, B′C′=6 cm,A′C′= cm
C.AB=10 cm,BC=AC=8 cm;A′B′= cm,B′C′=A′C′= cm
D.AB=1 cm,BC= cm,AC=3 cm;A′B′= cm,B′C′= cm,A′C′= cm知1-练3 已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当△DEF的另两边是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm B.4 cm,5 cm
C.5 cm,6 cm D.6 cm,7 cm知1-练2知识点网格上相似三角形的判定知2-讲例2 图1,图2中小正方形的边长均为1,则图2中的哪一个三角形(阴影部分)与图1中的△ABC相似?
导引:图中的三角形为格点三角形,可根据勾股定理求出
各边的长,然后根据三角形三边的长度的比是否相
等来判断哪两个三角形相似.图1图2解:由勾股定理知AC= ,BC=2,AB=
图2(1)中,三角形的三边长分别为1,
图2 (2)中,三角形的三边长分别为1,
图2 (3)中,三角形的三边长分别为
图2 (4)中,三角形的三边长分别为2,
∴图2 (2)中的三角形与△ABC相似.知2-讲知2-讲利用三角形三边对应成比例判定两三角形相似
的方法:首先把两个三角形的边分别按照从小到大的
顺序排列,找出两个三角形的对应边;再分别计算小、
中、大边的比,最后看三个比是否相等,若相等,则
两个三角形相似,否则不相似.
特别地,若三个比相等且等于1,则两个三角形
全等.(中考?荆州)如图,4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )知2-练如图,若A,B,C,P,Q,甲,乙,丙,丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲,乙,丙,丁四点中的( )
A.甲
B.乙
C.丙
D.丁知2-练1.学习时采用类比的方法进行,一方面可类比两个三
角形全等的判定方法,另一方面可类比上一课时中
有关两个三角形相似的判定方法.
2.利用三边成比例判定三角形相似的“三步骤”:
(1)排序:将三角形的边按大小顺序排列;
(2)计算:分别计算它们对应边的比值;
(3)判断:通过比值是否相等判断两个三角形是否
相似.
定三角形相似1课堂讲解三边成比例的两个三角形相似
网格上相似三角形的判定2课时流程逐点
导讲练课堂小结作业提升判定两个三角形全等我们有SSS的方法,类似地,判定两个三角形相似是否也有类似的简单方法呢?1知识点三边成比例的两个三角形相似知1-讲任意画一个三角形,再画另一个三角形,使它的各边长都是原来各边长的2倍,度量这两个三角形的对应角,他们对应相等吗?这两个三角形全等吗??问 题知1-讲如图,在△ABC和△A′B′C′中,
则△ABC与
△A′B′C′相似吗?为什么?
分析:这时可在A′B′上截取A′D=AB,再过D作DE//
B′C′,由△A′DE∽△A′B′C′,再证明△ABC
≌△A′DE,则可得到△ABC∽△A′B′C′.思 考知1-讲如图,在△ABC和△A'B'C'中,
求证: △ABC∽△A'B'C'. 证明:在线段A′B′(或它的延长线)上截取A′D=AB,过点D
作 DE//B′C′,交A′C′于点E.根据前面的定理,可得
△A′DE∽△A'B'C'.
∴DE=BC,A′E=AC.
∴ △A′DE≌△ABC.
∴△ABC ∽△A'B'C'.知1-讲 △A′DE是证明的中介,它把△ABC与△A′B′C′联系起来.知1-讲由此我们得到利用三边判定三角形相似的定理
(如图):
三边成比例的两个三角形相似.△ABC ∽△A'B'C'例1 根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
AB=4 cm,BC=6 cm,AC=8 cm,
A′B′= 12 cm,B′C′= 18 cm,A′C′=24 cm.?
解:
∴△ABC ∽△A'B'C'.
知1-讲知1-讲这个判定三角形相似的方法与三角形全等的判
定方法“边边边”十分相似,所不同的是在相似的
判定方法中的 “三边”要求的是“比相等”. 三边
的对应关系是“短∶短”“中∶中”“长∶长”.已知:如图,AD是△ABC的高,E,F分别是AB,AC的中点.求证:△DEF∽△ABC.知1-练若△ABC和△A′B′C′满足下列条件,其中使△ABC与△A′B′C′相似的是( )
A.AB=2.5 cm,BC=2 cm,AC=3 cm;A′B′=3 cm,B′C′=4 cm,A′C′=6 cm
B.AB=2 cm,BC=3 cm,AC=4 cm;A′B′=3 cm, B′C′=6 cm,A′C′= cm
C.AB=10 cm,BC=AC=8 cm;A′B′= cm,B′C′=A′C′= cm
D.AB=1 cm,BC= cm,AC=3 cm;A′B′= cm,B′C′= cm,A′C′= cm知1-练3 已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当△DEF的另两边是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm B.4 cm,5 cm
C.5 cm,6 cm D.6 cm,7 cm知1-练2知识点网格上相似三角形的判定知2-讲例2 图1,图2中小正方形的边长均为1,则图2中的哪一个三角形(阴影部分)与图1中的△ABC相似?
导引:图中的三角形为格点三角形,可根据勾股定理求出
各边的长,然后根据三角形三边的长度的比是否相
等来判断哪两个三角形相似.图1图2解:由勾股定理知AC= ,BC=2,AB=
图2(1)中,三角形的三边长分别为1,
图2 (2)中,三角形的三边长分别为1,
图2 (3)中,三角形的三边长分别为
图2 (4)中,三角形的三边长分别为2,
∴图2 (2)中的三角形与△ABC相似.知2-讲知2-讲利用三角形三边对应成比例判定两三角形相似
的方法:首先把两个三角形的边分别按照从小到大的
顺序排列,找出两个三角形的对应边;再分别计算小、
中、大边的比,最后看三个比是否相等,若相等,则
两个三角形相似,否则不相似.
特别地,若三个比相等且等于1,则两个三角形
全等.(中考?荆州)如图,4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )知2-练如图,若A,B,C,P,Q,甲,乙,丙,丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲,乙,丙,丁四点中的( )
A.甲
B.乙
C.丙
D.丁知2-练1.学习时采用类比的方法进行,一方面可类比两个三
角形全等的判定方法,另一方面可类比上一课时中
有关两个三角形相似的判定方法.
2.利用三边成比例判定三角形相似的“三步骤”:
(1)排序:将三角形的边按大小顺序排列;
(2)计算:分别计算它们对应边的比值;
(3)判断:通过比值是否相等判断两个三角形是否
相似.
