27.2.6 用两角相等关系判定三角形相似课件
文档属性
| 名称 | 27.2.6 用两角相等关系判定三角形相似课件 |  | |
| 格式 | zip | ||
| 文件大小 | 328.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 08:24:23 | ||
图片预览








文档简介
课件22张PPT。第二十七章 相似27.2 相似三角形第6课时 用两角相等关系
判定三角形相似1课堂讲解两角分别相等的两个三角形相似
两直角三角形相似的判定2课时流程逐点
导讲练课堂小结作业提升 小文同学不小心把学校实验室的玻璃打碎成三块,如图,现在,李文同学要到玻璃店去配一块完全一样的玻璃,为了省事,李文决定只带其中一块去做模型.
小颖说:带第①块去.
小明说:带第②块去.
小华说:带第③块去.
思考片刻后,李文同学决定接受小华的建议,带第③块去.这是因为在第③块中保留有原三角形的两角及夹边,果然,去配回的 三角形的玻璃与原三角形的玻璃一模一样,
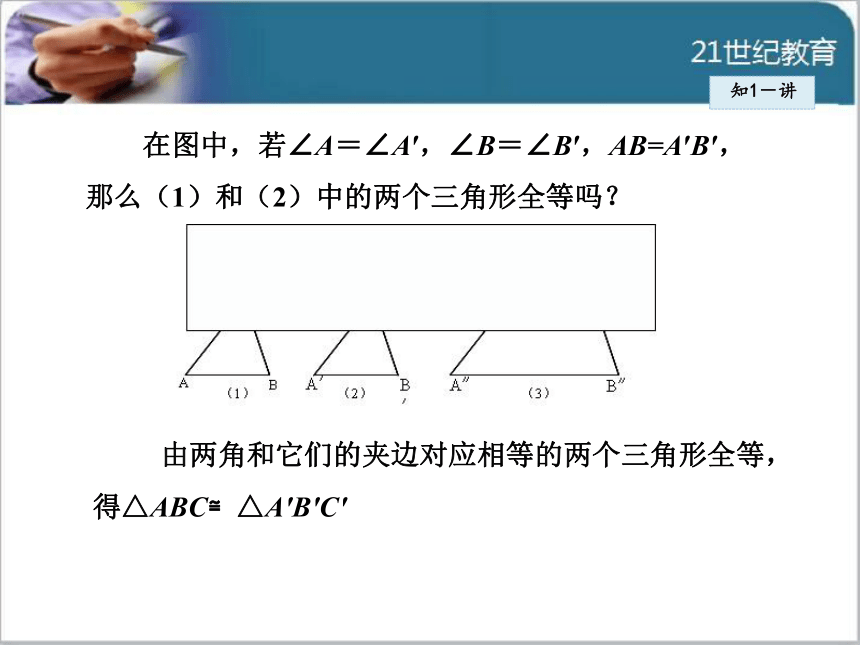
这件事给我们的启示是:有两角及夹边对应相等的两个三角形全等;那么,有两个角对应相等的三角形是否相似呢?相似三角形的判定是否有类似全等三角形的判定方法呢?1知识点两角分别相等的两个三角形相似知1-导 观察两副三角尺(如图),其中有同样两个锐角(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.知1-讲 在图中,若∠A=∠A′,∠B=∠B′,AB=A′B′,
那么(1)和(2)中的两个三角形全等吗?
由两角和它们的夹边对应相等的两个三角形全等,
得△ABC≌△A′B′C′知1-讲 若∠A=∠A″,∠B=∠B″, A″B″=2AB,那么(1)和(3)中的两个三角形相似吗?
由题意,图中的两个三角形的第3对角∠C=∠C″相等,同时通过度量可得B″C″=2BC,C″A″=2CA,这样由相似三角形的概念可知△A″B″C″∽△ABC;
知1-讲 由此能得出三角形相似的判定定理1:两个角
分别相等的两个三角形相似.
几何语言:
如图,在△ABC与△A′B′ C′,
∵∠A=∠A′,∠B=∠B′,
∴△ABC ∽ △A′B′C′. 例1 如图,Rt△ABC中,∠C=90°,AB=10,AC=8.E是AC上一
点,AE=5,ED⊥AB,垂足为D,求AD的长.知1-讲解:∵ ED⊥AB,
∴ ∠EDA=90°.
又∠C=90 °, ∠A=∠A,
∴△AED∽△ABC.
知1-讲 当两个三角形已具备一角对应相等的条件时,
往往先找是否有另一角对应相等,当此思路不通时,
再找夹等角的两边对应成比例.找角相等时应注意
挖掘公共角、对顶角、同角的余角(或补角)等.知1-练底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.12下列各组条件中,不能判定△ABC与△A′B′C′相似的是( )
A.∠A=∠A′,∠B=∠B′
B.∠C=∠C′=90°,∠A=35°,∠B′=55°
C.∠A=∠B,∠A′=∠B′
D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
知1-练3(2016·河北)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线
剪开,剪下的阴影三角形与原三
角形不相似的是( )
2知识点两直角三角形相似的判定知2-讲思考:
我们知道,两个直角三角形全等可以用“HL”来判定.
那么,满足斜边和一条直角边成比例的两个直角三角形相似
吗?
事实上,这两个直角三角形相似.下面我们给出证明.
如图,在Rt△ABC和Rt△A′B′C′中, ∠C=90°,
∠C′=90°,
求证: Rt△ABC∽Rt△A′B′C′ .
知2-讲分析:要证Rt△ABC∽Rt△A′B′C′ ,可设法证∴Rt△ABC∽Rt△A′B′C′.知2-讲直角三角形相似的判定定理:
(1)有一锐角相等的两个直角三角形相似;
(2)有两组直角边对应成比例的两直角三角形相似.
数学表达式:
在Rt△ABC和Rt△A′B′C′中,
(1)∵∠C=∠C′=90°,∠A=∠A′,∴Rt△ABC∽Rt△A′B′C′;
(2)∵∠C=∠C′=90°,
∴Rt△ABC∽Rt△A′B′C′.知2-讲直角三角形相似的判定方法:
有一锐角对应相等?两直角三角形相似
有两组直角边对应成比例?两直角三角形相似
有斜边与一直角边对应成比例?两直角三角形相似
知2-讲例2 在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条
件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
导引:根据相似三角形的判定方法对各个选项进行分析即可.
A.∵∠A=55°,∴∠B=90°-55°=35°.
∵∠D=35°,∴∠B=∠D.
又∵∠C=∠F=90°,∴△ABC∽△EDF;
C知2-讲B.∵AC=9,BC=12,DF=6,EF=8,
∴
又∵∠C=∠F=90°,∴△ABC∽△DEF;
C.由题目中知∠C=∠F=90°,但已知条件中不能得出两
组对应边成比例,故不能判定两三角形相似.
D.∵AB=10,AC=8,∴由勾股定理可得BC=6.
又DE=15,EF=9,∴
又∵∠C=∠F=90°,∴△ABC∽△DEF.
知2-讲 判定两直角三角形相似的方法:一个锐角对应相
等,两组直角边对应成比例,斜边和一直角边对应
成比例.知2-练如图,在△ABC与△ACD中,∠ACB=∠ADC=90°,AC= ,AD=2.当AB的长为多少时,△ABC与△ACD相似?
1知2-练(2015·安徽)如图,矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上,若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
2知2-练如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中:
①AC·BC=AB·CD;②AC2=AD·DB;③BC2=BD·BA;④CD2=AD·DB,正确的个数是( )
A.1
B.2
C.3
D.43 判定两三角形相似的思路:
(1)平行于三角形一边的直线,找两个三角形;
(2)已知一角对应相等,找另一角对应相等,或夹这个角的两边成
比例;
(3)已知两边对应成比例,找夹角相等,或与第三边成比例;
(4)已知等腰三角形,找顶角相等,或底角相等,或底、腰对应成
比例.
(5)已知直角三角形,找一组锐角相等,或两直角边对应成比例,
或斜边、一直角边对应成比例.
判定三角形相似1课堂讲解两角分别相等的两个三角形相似
两直角三角形相似的判定2课时流程逐点
导讲练课堂小结作业提升 小文同学不小心把学校实验室的玻璃打碎成三块,如图,现在,李文同学要到玻璃店去配一块完全一样的玻璃,为了省事,李文决定只带其中一块去做模型.
小颖说:带第①块去.
小明说:带第②块去.
小华说:带第③块去.
思考片刻后,李文同学决定接受小华的建议,带第③块去.这是因为在第③块中保留有原三角形的两角及夹边,果然,去配回的 三角形的玻璃与原三角形的玻璃一模一样,
这件事给我们的启示是:有两角及夹边对应相等的两个三角形全等;那么,有两个角对应相等的三角形是否相似呢?相似三角形的判定是否有类似全等三角形的判定方法呢?1知识点两角分别相等的两个三角形相似知1-导 观察两副三角尺(如图),其中有同样两个锐角(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.知1-讲 在图中,若∠A=∠A′,∠B=∠B′,AB=A′B′,
那么(1)和(2)中的两个三角形全等吗?
由两角和它们的夹边对应相等的两个三角形全等,
得△ABC≌△A′B′C′知1-讲 若∠A=∠A″,∠B=∠B″, A″B″=2AB,那么(1)和(3)中的两个三角形相似吗?
由题意,图中的两个三角形的第3对角∠C=∠C″相等,同时通过度量可得B″C″=2BC,C″A″=2CA,这样由相似三角形的概念可知△A″B″C″∽△ABC;
知1-讲 由此能得出三角形相似的判定定理1:两个角
分别相等的两个三角形相似.
几何语言:
如图,在△ABC与△A′B′ C′,
∵∠A=∠A′,∠B=∠B′,
∴△ABC ∽ △A′B′C′. 例1 如图,Rt△ABC中,∠C=90°,AB=10,AC=8.E是AC上一
点,AE=5,ED⊥AB,垂足为D,求AD的长.知1-讲解:∵ ED⊥AB,
∴ ∠EDA=90°.
又∠C=90 °, ∠A=∠A,
∴△AED∽△ABC.
知1-讲 当两个三角形已具备一角对应相等的条件时,
往往先找是否有另一角对应相等,当此思路不通时,
再找夹等角的两边对应成比例.找角相等时应注意
挖掘公共角、对顶角、同角的余角(或补角)等.知1-练底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.12下列各组条件中,不能判定△ABC与△A′B′C′相似的是( )
A.∠A=∠A′,∠B=∠B′
B.∠C=∠C′=90°,∠A=35°,∠B′=55°
C.∠A=∠B,∠A′=∠B′
D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
知1-练3(2016·河北)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线
剪开,剪下的阴影三角形与原三
角形不相似的是( )
2知识点两直角三角形相似的判定知2-讲思考:
我们知道,两个直角三角形全等可以用“HL”来判定.
那么,满足斜边和一条直角边成比例的两个直角三角形相似
吗?
事实上,这两个直角三角形相似.下面我们给出证明.
如图,在Rt△ABC和Rt△A′B′C′中, ∠C=90°,
∠C′=90°,
求证: Rt△ABC∽Rt△A′B′C′ .
知2-讲分析:要证Rt△ABC∽Rt△A′B′C′ ,可设法证∴Rt△ABC∽Rt△A′B′C′.知2-讲直角三角形相似的判定定理:
(1)有一锐角相等的两个直角三角形相似;
(2)有两组直角边对应成比例的两直角三角形相似.
数学表达式:
在Rt△ABC和Rt△A′B′C′中,
(1)∵∠C=∠C′=90°,∠A=∠A′,∴Rt△ABC∽Rt△A′B′C′;
(2)∵∠C=∠C′=90°,
∴Rt△ABC∽Rt△A′B′C′.知2-讲直角三角形相似的判定方法:
有一锐角对应相等?两直角三角形相似
有两组直角边对应成比例?两直角三角形相似
有斜边与一直角边对应成比例?两直角三角形相似
知2-讲例2 在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条
件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
导引:根据相似三角形的判定方法对各个选项进行分析即可.
A.∵∠A=55°,∴∠B=90°-55°=35°.
∵∠D=35°,∴∠B=∠D.
又∵∠C=∠F=90°,∴△ABC∽△EDF;
C知2-讲B.∵AC=9,BC=12,DF=6,EF=8,
∴
又∵∠C=∠F=90°,∴△ABC∽△DEF;
C.由题目中知∠C=∠F=90°,但已知条件中不能得出两
组对应边成比例,故不能判定两三角形相似.
D.∵AB=10,AC=8,∴由勾股定理可得BC=6.
又DE=15,EF=9,∴
又∵∠C=∠F=90°,∴△ABC∽△DEF.
知2-讲 判定两直角三角形相似的方法:一个锐角对应相
等,两组直角边对应成比例,斜边和一直角边对应
成比例.知2-练如图,在△ABC与△ACD中,∠ACB=∠ADC=90°,AC= ,AD=2.当AB的长为多少时,△ABC与△ACD相似?
1知2-练(2015·安徽)如图,矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上,若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
2知2-练如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中:
①AC·BC=AB·CD;②AC2=AD·DB;③BC2=BD·BA;④CD2=AD·DB,正确的个数是( )
A.1
B.2
C.3
D.43 判定两三角形相似的思路:
(1)平行于三角形一边的直线,找两个三角形;
(2)已知一角对应相等,找另一角对应相等,或夹这个角的两边成
比例;
(3)已知两边对应成比例,找夹角相等,或与第三边成比例;
(4)已知等腰三角形,找顶角相等,或底角相等,或底、腰对应成
比例.
(5)已知直角三角形,找一组锐角相等,或两直角边对应成比例,
或斜边、一直角边对应成比例.
