27.2.8 相似三角形的性质课件
图片预览











文档简介
课件30张PPT。第二十七章 相 似27.2 相似三角形第8课时 相似三角形
的性质1课堂讲解相似三角形对应线段的比
相似三角形周长的比
相似三角形面积的比2课时流程逐点
导讲练课堂小结作业提升 某社区拟筹资金 2000 元,在一块上、下底分别是 10米, 20米的梯形空地上种植花木,如图,他们想在△AMD 和 △BMC 地带种植单价为 10 元/平方米的太阳
花,当 △AMD 地带种满花后,已花了 500 元,请预算
一下,若继续在 △ BMC 地带种植同样的太阳花,资金
是否够用?1知识点相似三角形对应线段的比 三角形中有各种各样的几何量,例如三条边的长
度,三个内角的度数,高、中线、角平分线的长度,
以及周长、面积等.如果两个三角形相似,那么它们
的这些几何量之间有什么关系呢?知1-导问 题知1-导 探究:
如图,△ABC∽△A′B′C′,相似比为k,它们对应高、
对应中线、对应角平分线的比各是多少?
如图,分别作△ABC和 △A′B′C′的对应高AD和A′ D′ .知1-导∵ △ ABC∽△A′B′C′, ∴ ∠B= ∠B′ .
又△ ABD和△A′B′D′都是直角三角形,
∴△ ABD ∽ △A′B′D′.
∴
类似地,可以证明相似三角形对应中 线的比、
对应角平分线的比也等于 k.知1-导 这样,我们得到:
相似三角形对应高的比,对应中线的比与对应
角平分线的比都等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.例1 如图,在△ABC中,AD是BC边上的高,矩形
EFGH内接于△ABC,且长边FG在BC上,矩
形相邻两边的比为1∶2,若BC=30 cm,AD=
10 cm,求矩形EFGH的周长.
知1-讲导引:由四边形EFGH为矩形,得EH∥BC,所以△AEH
与△ABC相似,根据相似三角形对应高的比等于相
似比可求出HG的长,进而求出EH的长,即可求得
矩形EFGH的周长.
解:设HG=x cm,则EH=2x cm. 易得AP⊥EH.
∵AD=10 cm,∴AP=(10-x) cm.
∵四边形EFGH为矩形,∴EH∥BC,
∴△AEH ∽ △ABC.∴
解得x=6.∴HG=6 cm,EH=12 cm.
∴矩形EFGH的周长为36 cm.
知1-讲知1-讲 相似三角形中对应线段的比等于相似比,其中
“对应线段”除对应边外,还有对应边上的高、中
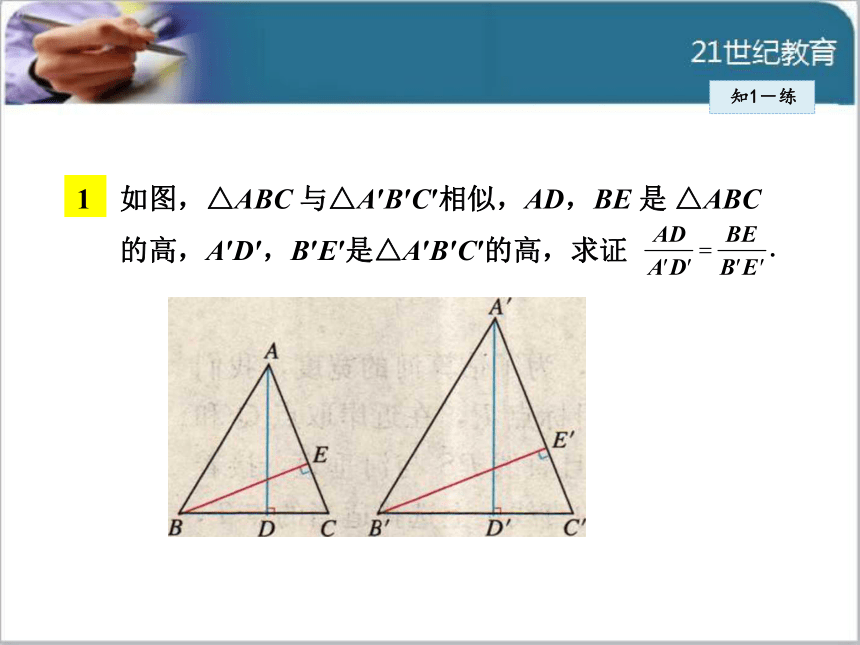
线,对应角的平分线.如图,△ABC 与△A′B′C′相似,AD,BE 是 △ABC 的高,A′D′,B′E′是△A′B′C′的高,求证知1-练2 (2016?兰州)已知△ABC∽△DEF,若△ABC与
△DEF的相似比为 ,则△ABC与△DEF对应
中线的比为( )
A. B. C. D.
已知△ABC∽△A′B′C′,BD和B′D′分别是两个
三角形对应角的平分线,且AC∶A′C′=2∶3,
若BD=4 cm,则B′D′的长是( )
A.3 cm B.4 cm C.6 cm D.8 cm
知1-练2知识点相似三角形周长的比知2-导 某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽,绿地被削
去了一个角,变成了一个梯形,
原绿化地一边AB的长由原来的
30米缩短成18米(如图).现在的
问题是:它的周长是多少?问 题知2-导解答:将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30 m,BD=18 m,
△ABC 的周长为80 m,求△ADE的周长.
知2-导∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,∴
由比例的性质可得,
而△ADE 的周长=AD+AE+DE,
△ABC的周长=AB+AC+BC,
∴
∴△ADE 的周长=32 m.知2-导 从以上解答过程中可以看出:相似三角形的周
长比等于相似比.知2-讲例2 已知两个相似三角形的最短边分别为9 cm和
6 cm. 若它们的周长之和为60 cm,则这两个
三角形的周长分别是多少?
导引:两个相似三角形的最短边就是一组对应边,
由此可确定相似比,进而根据已知条件,解
以一个三角形周长为未知数的方程即可.知2-讲解:设△ABC∽△A1B1C1,且△ABC中的最短边
AC=9 cm,△A1B1C1中的最短边A1C1=6 cm.
则
∴△ABC和△A1B1C1的相似比为
设△ABC的周长为x cm,
则△A1B1C1的周长为(60-x)cm.
∴
∴△ABC的周长为36 cm,△A1B1C1的周长为24 cm.解得x=36,60-x=24.知2-讲 相似三角形周长的比等于相似比.在解题时,如
果是相似图形,求周长就常用到周长比等于相似比. 两个相似三角形对应中线的比是2∶3,周长的和
是20,则两个三角形的周长分别为( )
A. 8和12 B. 9和11
C. 7和13 D. 6和14知2-练知2-练2 (2016?重庆)△ABC与△DEF的相似比为1∶4,则
△ABC与△DEF的周长比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶16
已知△ABC∽△DEF,相似比为3∶1,且△ABC
的周长为18,则△DEF的周长为( )
A.2 B.3 C.6 D.54知3-导3知识点相似三角形面积的比相似三角形面积的比与相似比有什么关系?
如图,由前面的结论,我们有问 题知3-导这样,我们得到:
相似三角形面积的比等于相似比的平方.例3 如图,在△ABC和△DEF 中,AB = 2DE,AC =
2DF,∠A=∠D. 若△ABC的边BC上的高为6,
面积为 ,求△DEF的边EF 上的高和面积.知3-讲解: 在△ABC和△DEF中,
∵ AB = 2DE,AC = 2DF,
∴
又 ∠D=∠A,
∴ △DEF∽△ABC,△DEF 与△ABC 的相似比为
∵△ABC的边BC上的高为6,面积为
∴△DEF的边EF上的高为
面积为?知3-讲知3-讲 利用相似比求周长和面积时,先判定两个三角形
相似,然后找准相似比,利用“相似三角形周长的比
等于相似比,相似三角形面积的比等于相似比的平方”
解题.警示:不要误认为面积的比等于相似比.1 判断题(正确的画“√”,错误的画“×”).
(1) 一个三角形的各边长扩大为原来的5倍,这个三
角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三
角形的面积也扩大为原来的9倍. ( )
知3-练2 (2016?临夏州)如果两个相似三角形的面积比是1∶4,
那么它们的周长比是( )
A.1∶16 B.1∶4 C.1∶6 D.1∶2
3 (2015?酒泉)如图,D,E分别是△ABC的边AB,BC
上的点,DE∥AC,若S△BDE∶S△CDE=1∶3,则
S△DOE∶S△AOC的值为( )
A. B.
C. D.知3-练
的性质1课堂讲解相似三角形对应线段的比
相似三角形周长的比
相似三角形面积的比2课时流程逐点
导讲练课堂小结作业提升 某社区拟筹资金 2000 元,在一块上、下底分别是 10米, 20米的梯形空地上种植花木,如图,他们想在△AMD 和 △BMC 地带种植单价为 10 元/平方米的太阳
花,当 △AMD 地带种满花后,已花了 500 元,请预算
一下,若继续在 △ BMC 地带种植同样的太阳花,资金
是否够用?1知识点相似三角形对应线段的比 三角形中有各种各样的几何量,例如三条边的长
度,三个内角的度数,高、中线、角平分线的长度,
以及周长、面积等.如果两个三角形相似,那么它们
的这些几何量之间有什么关系呢?知1-导问 题知1-导 探究:
如图,△ABC∽△A′B′C′,相似比为k,它们对应高、
对应中线、对应角平分线的比各是多少?
如图,分别作△ABC和 △A′B′C′的对应高AD和A′ D′ .知1-导∵ △ ABC∽△A′B′C′, ∴ ∠B= ∠B′ .
又△ ABD和△A′B′D′都是直角三角形,
∴△ ABD ∽ △A′B′D′.
∴
类似地,可以证明相似三角形对应中 线的比、
对应角平分线的比也等于 k.知1-导 这样,我们得到:
相似三角形对应高的比,对应中线的比与对应
角平分线的比都等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.例1 如图,在△ABC中,AD是BC边上的高,矩形
EFGH内接于△ABC,且长边FG在BC上,矩
形相邻两边的比为1∶2,若BC=30 cm,AD=
10 cm,求矩形EFGH的周长.
知1-讲导引:由四边形EFGH为矩形,得EH∥BC,所以△AEH
与△ABC相似,根据相似三角形对应高的比等于相
似比可求出HG的长,进而求出EH的长,即可求得
矩形EFGH的周长.
解:设HG=x cm,则EH=2x cm. 易得AP⊥EH.
∵AD=10 cm,∴AP=(10-x) cm.
∵四边形EFGH为矩形,∴EH∥BC,
∴△AEH ∽ △ABC.∴
解得x=6.∴HG=6 cm,EH=12 cm.
∴矩形EFGH的周长为36 cm.
知1-讲知1-讲 相似三角形中对应线段的比等于相似比,其中
“对应线段”除对应边外,还有对应边上的高、中
线,对应角的平分线.如图,△ABC 与△A′B′C′相似,AD,BE 是 △ABC 的高,A′D′,B′E′是△A′B′C′的高,求证知1-练2 (2016?兰州)已知△ABC∽△DEF,若△ABC与
△DEF的相似比为 ,则△ABC与△DEF对应
中线的比为( )
A. B. C. D.
已知△ABC∽△A′B′C′,BD和B′D′分别是两个
三角形对应角的平分线,且AC∶A′C′=2∶3,
若BD=4 cm,则B′D′的长是( )
A.3 cm B.4 cm C.6 cm D.8 cm
知1-练2知识点相似三角形周长的比知2-导 某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽,绿地被削
去了一个角,变成了一个梯形,
原绿化地一边AB的长由原来的
30米缩短成18米(如图).现在的
问题是:它的周长是多少?问 题知2-导解答:将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30 m,BD=18 m,
△ABC 的周长为80 m,求△ADE的周长.
知2-导∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,∴
由比例的性质可得,
而△ADE 的周长=AD+AE+DE,
△ABC的周长=AB+AC+BC,
∴
∴△ADE 的周长=32 m.知2-导 从以上解答过程中可以看出:相似三角形的周
长比等于相似比.知2-讲例2 已知两个相似三角形的最短边分别为9 cm和
6 cm. 若它们的周长之和为60 cm,则这两个
三角形的周长分别是多少?
导引:两个相似三角形的最短边就是一组对应边,
由此可确定相似比,进而根据已知条件,解
以一个三角形周长为未知数的方程即可.知2-讲解:设△ABC∽△A1B1C1,且△ABC中的最短边
AC=9 cm,△A1B1C1中的最短边A1C1=6 cm.
则
∴△ABC和△A1B1C1的相似比为
设△ABC的周长为x cm,
则△A1B1C1的周长为(60-x)cm.
∴
∴△ABC的周长为36 cm,△A1B1C1的周长为24 cm.解得x=36,60-x=24.知2-讲 相似三角形周长的比等于相似比.在解题时,如
果是相似图形,求周长就常用到周长比等于相似比. 两个相似三角形对应中线的比是2∶3,周长的和
是20,则两个三角形的周长分别为( )
A. 8和12 B. 9和11
C. 7和13 D. 6和14知2-练知2-练2 (2016?重庆)△ABC与△DEF的相似比为1∶4,则
△ABC与△DEF的周长比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶16
已知△ABC∽△DEF,相似比为3∶1,且△ABC
的周长为18,则△DEF的周长为( )
A.2 B.3 C.6 D.54知3-导3知识点相似三角形面积的比相似三角形面积的比与相似比有什么关系?
如图,由前面的结论,我们有问 题知3-导这样,我们得到:
相似三角形面积的比等于相似比的平方.例3 如图,在△ABC和△DEF 中,AB = 2DE,AC =
2DF,∠A=∠D. 若△ABC的边BC上的高为6,
面积为 ,求△DEF的边EF 上的高和面积.知3-讲解: 在△ABC和△DEF中,
∵ AB = 2DE,AC = 2DF,
∴
又 ∠D=∠A,
∴ △DEF∽△ABC,△DEF 与△ABC 的相似比为
∵△ABC的边BC上的高为6,面积为
∴△DEF的边EF上的高为
面积为?知3-讲知3-讲 利用相似比求周长和面积时,先判定两个三角形
相似,然后找准相似比,利用“相似三角形周长的比
等于相似比,相似三角形面积的比等于相似比的平方”
解题.警示:不要误认为面积的比等于相似比.1 判断题(正确的画“√”,错误的画“×”).
(1) 一个三角形的各边长扩大为原来的5倍,这个三
角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三
角形的面积也扩大为原来的9倍. ( )
知3-练2 (2016?临夏州)如果两个相似三角形的面积比是1∶4,
那么它们的周长比是( )
A.1∶16 B.1∶4 C.1∶6 D.1∶2
3 (2015?酒泉)如图,D,E分别是△ABC的边AB,BC
上的点,DE∥AC,若S△BDE∶S△CDE=1∶3,则
S△DOE∶S△AOC的值为( )
A. B.
C. D.知3-练
