27.3.1 位似图形课件
图片预览







文档简介
课件30张PPT。第二十七章 相 似27.3 位 似第1课时 位似图形1课堂讲解位似图形的定义
位似图形的性质
位似图形的画法2课时流程逐点
导讲练课堂小结作业提升 用一个带有小孔的板遮挡在屏幕与物之间,屏幕上就会形成物的倒像,我们把这样的现象叫小孔成像.前后移动中间的板,屏幕上像的大小也会随之发生变化.这种现象反映了光沿直线传播的性质.
同时,我们可以发现,像与实物是两个相似的图形,而且它们对应点的连线都过一个点,
我们可以说它们是位似图形.生
活中还有哪些图形是位似图形呢?
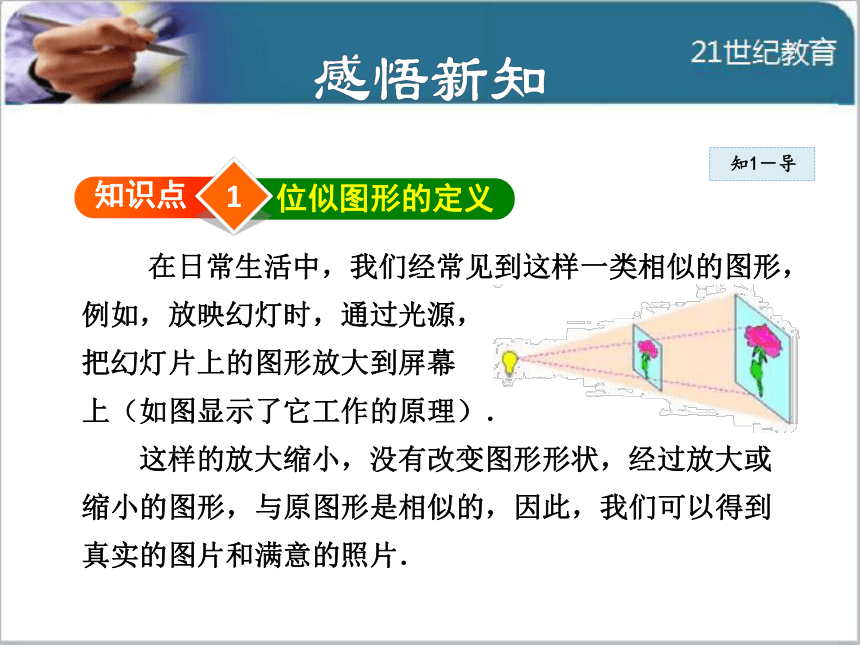
快来学习本节课内容吧!1知识点位似图形的定义 在日常生活中,我们经常见到这样一类相似的图形,
例如,放映幻灯时,通过光源,
把幻灯片上的图形放大到屏幕
上(如图显示了它工作的原理).
这样的放大缩小,没有改变图形形状,经过放大或
缩小的图形,与原图形是相似的,因此,我们可以得到
真实的图片和满意的照片.知1-导知1-导 下面,我们来研究这类相似的图形.
如图,如果一个图形上的点A,B,
…,P,…和另一个图形上的点A′,B′,
…,P′,…分别对应,并且它们的连线
AA′,BB′,…,PP′,…都经过同一点
O,
两个图形叫做位似图形(homothetic figures),点O是位似
中心.位似图 形不仅相似,而且具有特殊的位置关系.那么这知1-导 两个多边形不仅相似,而且对应顶点的连线相
交于一点,像这样的两个图形叫做位似图形,这点
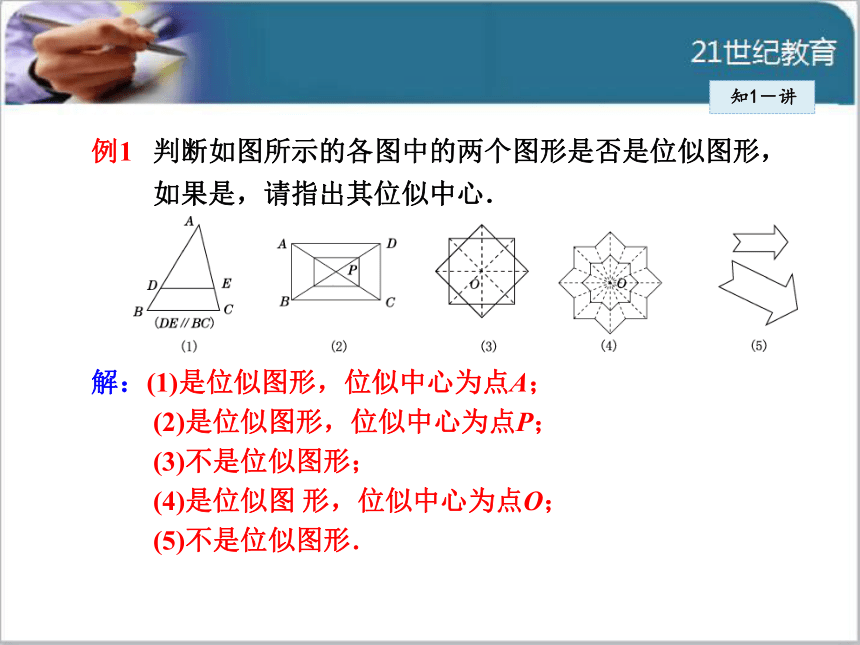
叫做位似中心 .例1 判断如图所示的各图中的两个图形是否是位似图形,
如果是,请指出其位似中心.
解:(1)是位似图形,位似中心为点A;
(2)是位似图形,位似中心为点P;
(3)不是位似图形;
(4)是位似图 形,位似中心为点O;
(5)不是位似图形.知1-讲知1-讲1. (1)位似图形必须同时满足:
①两个图形是相似图形;
②两个相似图形的每组对应点的连线都经过同一点;
二者缺一不可.
(2)位似中心可能在两个位似图形的一侧,也可能在两
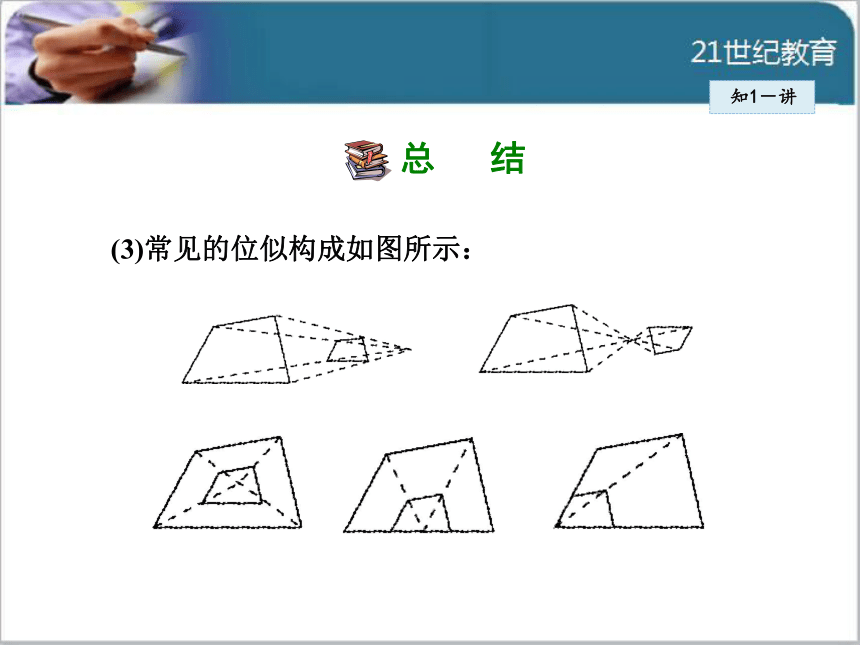
个位似图形之间.知1-讲(3)常见的位似构成如图所示:
知1-讲2. 位似与相似的关系:
(1)相似仅要求两个图形形状完全相同,而位似是在
相似的基础上要求对应顶点的连线相交于一点.
(2)如果两个图形是位似图形,那么这两个图形必是
相似图形,但是相似的两个图形不一定是位似图
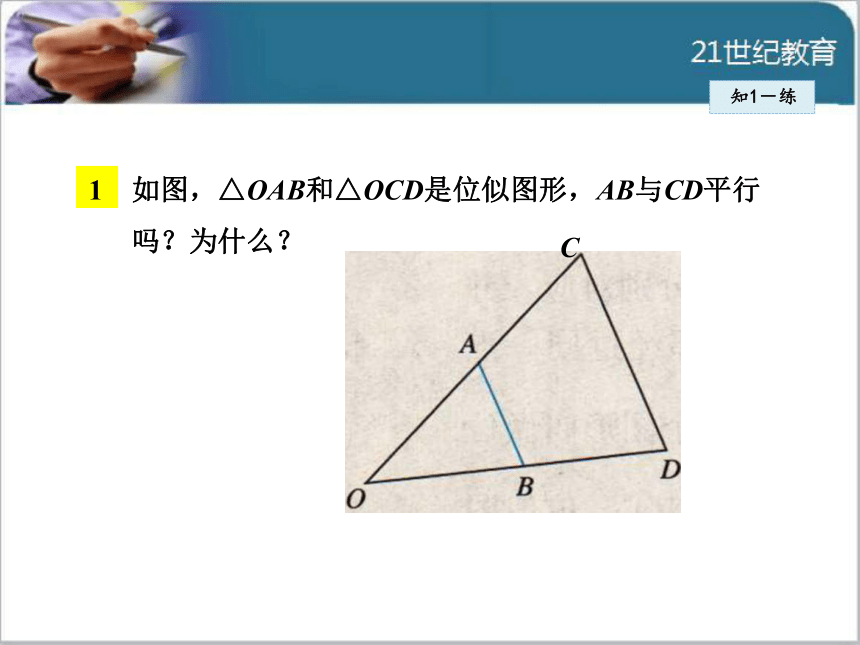
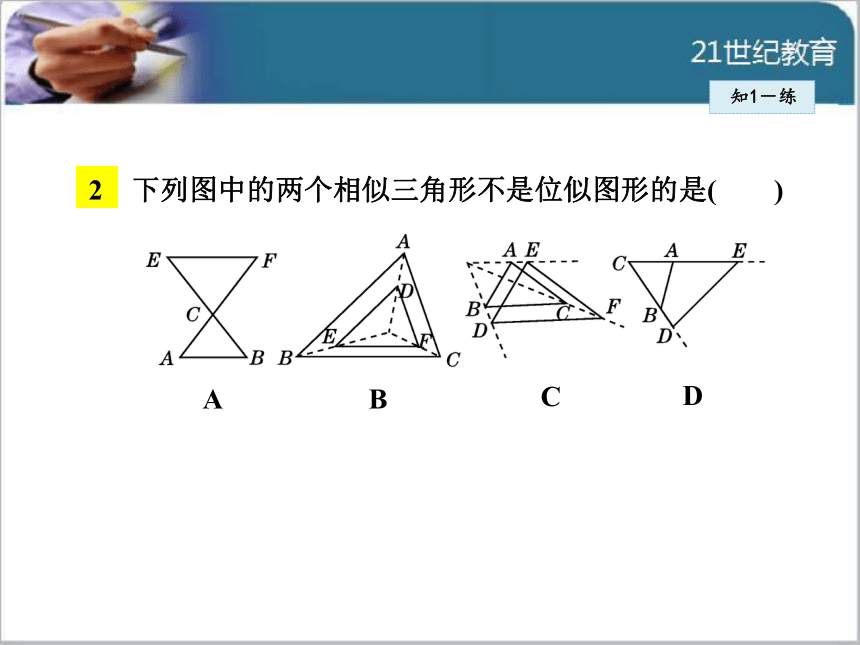
形,因此位似是相似的特殊情况.如图,△OAB和△OCD是位似图形,AB与CD平行吗?为什么?知1-练下列图中的两个相似三角形不是位似图形的是( )知1-练ACDB3 图中两个四边形是位似图形,它们的位似中心是( )
A.点M
B.点N
C.点O
D.点P知1-练2知识点位似图形的性质知2-讲 图中有多边形相似吗?如果有,那么这种相似有
什么特征?知2-讲(1)位似图形对应顶点的连线必过位似中心.
(2)位似图形任意一组对应点到位似中心的距离之比等于
相似比.
(3)位似图形的对应线段平行(或在一条直线上),且对应
线段之比相等.
(4)两个图形位似,则两个图形必相似,其相似比等于位
似比,周长比等于位似比,面积比等于位似比的平方.知2-讲例2 〈玉林〉△ABC与△A′B′C′是位似图形,且△ABC
与△A′B′C′的位似比是1∶2,已知△ABC的面积是3,
则△A′B′C′的面积是( )
A. 3 B. 6 C. 9 D. 12
导引:∵△ABC与△A′B′C′是位似图形,且△ABC与
△A′B′C′的位似比是1∶2,
∴△ABC与△A′B′C′相似,且相似比为1∶2.
∴△ABC与△A′B′C′的面积比为1∶4.
∵△ABC的面积是3,∴△A′B′C′的面积是12. D知2-讲 两个图形位似,则两个图形相似,所以相似图
形的性质,位似图形都满足,可以直接运用.1 〈沈阳〉如图,△ABC与△DEF位似,位似中心为
点O,且△ABC的面积等于△DEF面积的 ,则
AB∶DE=________.知2-练知2-练2 (2016?十堰)如图,以点O为位似中心,将△ABC缩
小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′
与△ABC的面积比为( )
A.1∶3 B.1∶4 C.1∶5 D.1∶9知2-练如图,点O是五边形ABCDE和A1B1C1D1E1的位似
中心,若OA∶OA1=1∶3,则C1D1∶CD=( )
A.1∶2 B.1∶3 C.3∶1 D.1∶4知3-导3知识点位似图形的画法 探究:
如果在四边形ABCD外任取一点O,分别在OA,QB,
OC,OD的反向延长线上取点A′ ,B′ ,C′ ,D′ ,使得
四边形A′B′C′D′ 与四边形
ABCD有什么关系?如果点O取在四边形ABCD内部呢?
分别画出得到的四边形A′B′C′D′ .知3-导 例如,要把四边形ABCD缩小到原来的
以在四边形ABCD外任取一点O(如图),分别在线段
OA,OB,OC,OD上取点A′ ,B′ ,C′ ,D′ ,使得
顺次连接点A′ ,B′ ,C′ ,
D′, 所得四边形A′B′C′D′就是所要求的图形 .我们可知3-讲画位似多边形的一般步骤:
(1)确定位似中心;
(2)分别连接位似中心和能代
表原多边形的关键点;
(3)根据位似比,利用截取的方法,找出所作的位似
多边形的对应点;
(4)顺次连接上述各点,得到放大或缩小的多边形.
例3 如图,在6×8网格图中,每个小正方形边长均为1,
点O和△ABC的顶点均为小正方形的顶点.
(1)以O为位似中心,在网格图中作△A′B′C′,使
△A′B′C′和△ABC位似,且位似比为 1∶2;
(2) 连接(1)中的AA′,求四边形AA′C′C的周长.
(结果保留根号)知3-讲分析:(1)根据位似比是1∶2,画出以O为位似中心的△A′B′C′;
(2)根据勾股定理求出AC,A′C′的长,由于 AA′,CC′
的长易得,相加即可求得四边形AA′C′C的周长.
解:(1)如图所示:
(2)AA′=CC′=2.
在Rt△OA′C′中,
OA′=OC′=2,得A′C′=
同理可得AC=
∴四边形AA′C′C的周长=知3-讲知3-讲画位似图形的步骤:
第一步:确定位似中心O(位似中心可以在图形外部,
也可以在图形内部,还可以在图形的边上,
还可以在某一个顶点上);
第二步:画出图形各顶点与位似中心O的连线;
第三步:按相似比取点;
第四步:顺次连接各点,所得的图形就是所求的图形.知3-讲(1)位似中心的选取要使画图方便且符合要求,一般以多
边形的一个顶点为位似中心画图最简便.
(2)画位似图形时,要弄清相似比,即分清是已知图形与新
图形的相似比,还是新图形与已知图形的相似比.
(3)一般情况下,画已知图形的位似图形的结果不唯一.1 如图,以点O为位似中心,将△ ABC放大为原来的3倍.知3-练如图是△ABC位似图形的几种画法,其中正确的
有( )
A.1个 B.2个 C.3个 D.4个知3-练位似图形的概念包括四层内容:
(1)位似图形是针对两个图形而言的;
(2)位似图形是相似图形;
(3)位似图形的每组对应点所在的直线都必须经过同一个点;
(4)位似图形反映了两个图形特殊的形状和位置关系,位似
图形一定是相似图形,而相似图形未必是位似图形,两
者的区别在于:位似图形有位似中心,而相似图形不一
定有位似中心.
位似图形的性质
位似图形的画法2课时流程逐点
导讲练课堂小结作业提升 用一个带有小孔的板遮挡在屏幕与物之间,屏幕上就会形成物的倒像,我们把这样的现象叫小孔成像.前后移动中间的板,屏幕上像的大小也会随之发生变化.这种现象反映了光沿直线传播的性质.
同时,我们可以发现,像与实物是两个相似的图形,而且它们对应点的连线都过一个点,
我们可以说它们是位似图形.生
活中还有哪些图形是位似图形呢?
快来学习本节课内容吧!1知识点位似图形的定义 在日常生活中,我们经常见到这样一类相似的图形,
例如,放映幻灯时,通过光源,
把幻灯片上的图形放大到屏幕
上(如图显示了它工作的原理).
这样的放大缩小,没有改变图形形状,经过放大或
缩小的图形,与原图形是相似的,因此,我们可以得到
真实的图片和满意的照片.知1-导知1-导 下面,我们来研究这类相似的图形.
如图,如果一个图形上的点A,B,
…,P,…和另一个图形上的点A′,B′,
…,P′,…分别对应,并且它们的连线
AA′,BB′,…,PP′,…都经过同一点
O,
两个图形叫做位似图形(homothetic figures),点O是位似
中心.位似图 形不仅相似,而且具有特殊的位置关系.那么这知1-导 两个多边形不仅相似,而且对应顶点的连线相
交于一点,像这样的两个图形叫做位似图形,这点
叫做位似中心 .例1 判断如图所示的各图中的两个图形是否是位似图形,
如果是,请指出其位似中心.
解:(1)是位似图形,位似中心为点A;
(2)是位似图形,位似中心为点P;
(3)不是位似图形;
(4)是位似图 形,位似中心为点O;
(5)不是位似图形.知1-讲知1-讲1. (1)位似图形必须同时满足:
①两个图形是相似图形;
②两个相似图形的每组对应点的连线都经过同一点;
二者缺一不可.
(2)位似中心可能在两个位似图形的一侧,也可能在两
个位似图形之间.知1-讲(3)常见的位似构成如图所示:
知1-讲2. 位似与相似的关系:
(1)相似仅要求两个图形形状完全相同,而位似是在
相似的基础上要求对应顶点的连线相交于一点.
(2)如果两个图形是位似图形,那么这两个图形必是
相似图形,但是相似的两个图形不一定是位似图
形,因此位似是相似的特殊情况.如图,△OAB和△OCD是位似图形,AB与CD平行吗?为什么?知1-练下列图中的两个相似三角形不是位似图形的是( )知1-练ACDB3 图中两个四边形是位似图形,它们的位似中心是( )
A.点M
B.点N
C.点O
D.点P知1-练2知识点位似图形的性质知2-讲 图中有多边形相似吗?如果有,那么这种相似有
什么特征?知2-讲(1)位似图形对应顶点的连线必过位似中心.
(2)位似图形任意一组对应点到位似中心的距离之比等于
相似比.
(3)位似图形的对应线段平行(或在一条直线上),且对应
线段之比相等.
(4)两个图形位似,则两个图形必相似,其相似比等于位
似比,周长比等于位似比,面积比等于位似比的平方.知2-讲例2 〈玉林〉△ABC与△A′B′C′是位似图形,且△ABC
与△A′B′C′的位似比是1∶2,已知△ABC的面积是3,
则△A′B′C′的面积是( )
A. 3 B. 6 C. 9 D. 12
导引:∵△ABC与△A′B′C′是位似图形,且△ABC与
△A′B′C′的位似比是1∶2,
∴△ABC与△A′B′C′相似,且相似比为1∶2.
∴△ABC与△A′B′C′的面积比为1∶4.
∵△ABC的面积是3,∴△A′B′C′的面积是12. D知2-讲 两个图形位似,则两个图形相似,所以相似图
形的性质,位似图形都满足,可以直接运用.1 〈沈阳〉如图,△ABC与△DEF位似,位似中心为
点O,且△ABC的面积等于△DEF面积的 ,则
AB∶DE=________.知2-练知2-练2 (2016?十堰)如图,以点O为位似中心,将△ABC缩
小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′
与△ABC的面积比为( )
A.1∶3 B.1∶4 C.1∶5 D.1∶9知2-练如图,点O是五边形ABCDE和A1B1C1D1E1的位似
中心,若OA∶OA1=1∶3,则C1D1∶CD=( )
A.1∶2 B.1∶3 C.3∶1 D.1∶4知3-导3知识点位似图形的画法 探究:
如果在四边形ABCD外任取一点O,分别在OA,QB,
OC,OD的反向延长线上取点A′ ,B′ ,C′ ,D′ ,使得
四边形A′B′C′D′ 与四边形
ABCD有什么关系?如果点O取在四边形ABCD内部呢?
分别画出得到的四边形A′B′C′D′ .知3-导 例如,要把四边形ABCD缩小到原来的
以在四边形ABCD外任取一点O(如图),分别在线段
OA,OB,OC,OD上取点A′ ,B′ ,C′ ,D′ ,使得
顺次连接点A′ ,B′ ,C′ ,
D′, 所得四边形A′B′C′D′就是所要求的图形 .我们可知3-讲画位似多边形的一般步骤:
(1)确定位似中心;
(2)分别连接位似中心和能代
表原多边形的关键点;
(3)根据位似比,利用截取的方法,找出所作的位似
多边形的对应点;
(4)顺次连接上述各点,得到放大或缩小的多边形.
例3 如图,在6×8网格图中,每个小正方形边长均为1,
点O和△ABC的顶点均为小正方形的顶点.
(1)以O为位似中心,在网格图中作△A′B′C′,使
△A′B′C′和△ABC位似,且位似比为 1∶2;
(2) 连接(1)中的AA′,求四边形AA′C′C的周长.
(结果保留根号)知3-讲分析:(1)根据位似比是1∶2,画出以O为位似中心的△A′B′C′;
(2)根据勾股定理求出AC,A′C′的长,由于 AA′,CC′
的长易得,相加即可求得四边形AA′C′C的周长.
解:(1)如图所示:
(2)AA′=CC′=2.
在Rt△OA′C′中,
OA′=OC′=2,得A′C′=
同理可得AC=
∴四边形AA′C′C的周长=知3-讲知3-讲画位似图形的步骤:
第一步:确定位似中心O(位似中心可以在图形外部,
也可以在图形内部,还可以在图形的边上,
还可以在某一个顶点上);
第二步:画出图形各顶点与位似中心O的连线;
第三步:按相似比取点;
第四步:顺次连接各点,所得的图形就是所求的图形.知3-讲(1)位似中心的选取要使画图方便且符合要求,一般以多
边形的一个顶点为位似中心画图最简便.
(2)画位似图形时,要弄清相似比,即分清是已知图形与新
图形的相似比,还是新图形与已知图形的相似比.
(3)一般情况下,画已知图形的位似图形的结果不唯一.1 如图,以点O为位似中心,将△ ABC放大为原来的3倍.知3-练如图是△ABC位似图形的几种画法,其中正确的
有( )
A.1个 B.2个 C.3个 D.4个知3-练位似图形的概念包括四层内容:
(1)位似图形是针对两个图形而言的;
(2)位似图形是相似图形;
(3)位似图形的每组对应点所在的直线都必须经过同一个点;
(4)位似图形反映了两个图形特殊的形状和位置关系,位似
图形一定是相似图形,而相似图形未必是位似图形,两
者的区别在于:位似图形有位似中心,而相似图形不一
定有位似中心.
