28.1.4 一般角的三角函数值课件
图片预览








文档简介
课件28张PPT。第二十八章 锐角三角函数28.1 锐角三角函数第4课时 一般角的三角
函数值1课堂讲解用计算器求已知锐角的三角函数值
用计算器求已知三角函数值的对应角
用计算器探究三角函数的性质2课时流程逐点
导讲练课堂小结作业提升 要测量教学楼的高度,小英身高1.6m.她在距离教学楼30m处测得仰角为25°,你能借助计算器估算出教学楼的高度吗?(精确到0.1m)1知识点用计算器求已知锐角的三角函数值 通过上面的学习,我们知道,当锐角A是 30°,45°或60°等特殊角时,可以求得这些
特殊角的 锐角三角函数值;如果锐角A不是这
些特殊角, 怎样得到它的锐角三角函数值呢?知1-讲知1-讲 我们可以借助计算器求锐角三角函数值.
例如求sin18°,利用计算器的 键,并输入角
度值18,得到结果sin18°=0.309 016 994.
又如求tan30°36′,利用 键,并输入角的度、
分值(可以使用 键),就可以得到结果
0.591 398 351.
因为30°36′=30.6°,所以也可以利用 键,并
输入角度值30.6,同样得到结果0.591 398 351.sintan°′ ″tan知1-讲利用计算器求锐角三角函数值:
1. 当锐角的大小以度为单位时,可先按 , ,
键,然后输入角度值(可以是整数,也可以是
小数),最后按 键,就可以在显示屏上显示出
结果;
2. 当锐角的大小以度、分、秒为单位时要借助
键计算,按键顺序是: (或 、 )、度数、
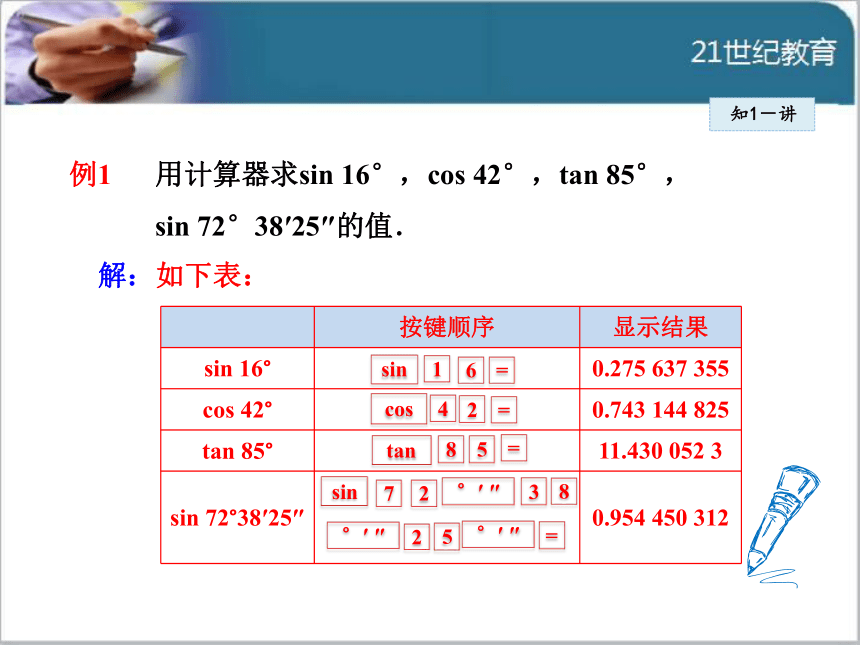
、分数、 、秒数、 、 .sincostan=°′ ″sincostan°′ ″°′ ″°′ ″= 例1 用计算器求sin 16°,cos 42°,tan 85°,
sin 72°38′25″的值.知1-讲解:如下表:sintansin164cos285252738====°′ ″°′ ″°′ ″知1-讲 要注意不同型号的计算器的操
作步骤可能有所不同.1 用计算器求下列锐角三角函数值:
(1)sin 20°,cos 70°;
sin 35°, cos 55°;
sin15°32′,cos74°28′;
(2)tan 3° 8',tan 80° 25′43".知1-练 分析第1(1)题的结果,你能得出什么猜想?你能说明自己的猜想吗?知1-练(2016·烟台)如图,是我们数学课上采用的科学计
算器面板,利用该型号计算器计算 cos 55°,
按键顺序正确的是( )
A.
B.
C.
D.
利用计算器求sin 30°时,依次按键
,则计算器上显示的结果是( )
A.0.5 B.0.707 C.0.866 D.1sin30°′ ″=cos255×=cos2550=cos255=cos255=2知识点用计算器求已知三角函数值的对应角知2-讲 如果已知锐角三角函数值,也可以使用计算
器求出相应锐角的度数.
例如,已知sin A=0. 501 8,用计算器求锐角A
可以按照下面方法操作:
依次按键 ,然后输入函数值
0.501 8,得到∠A=30.119 158 67° (这说明锐角A
精确到1°的结果为30°)..sin2nd F知2-讲 还可以利用 键,进一步得
到∠A=30 °07′08.97″(这说明锐角A精确到
1′的结果为30°7′,精确到 1"的结果为30°
7′9″)..2nd F°′ ″知2-讲已知锐角三角函数值求锐角的度数:
如果是特殊角(30°, 45°,60°)的三角函
数值,可直接写出其相应的角的度数;若不是特殊
角的三角函数值,应利用计算器求角的度数.求角
的度数要先按 键,将 、 、 转化
成它们的第二功能键;当三角函数值为分数时,应
先化成小数.2nd Fsincostan知2-讲例2 已知下列锐角三角函数值,用计算器求
其相应的锐角:
(1)sin A=0.516 8(结果精确到0.01°);
(2)cos A=0.675 3(结果精确到1″);
(3)tan A=0.189(结果精确到1°)..导引:已知锐角三角函数值,利用计算器求锐
角的度数时要注意先按 键.2nd F知2-讲解:(1)依次按键:
显示结果为:31.117 845 56,即∠A≈31.12°.
(2)依次按键:
显示结果为:47°31′21.18″,
即 ∠A≈47°31′21″.
(3)依次按键:
显示结果为:10.702 657 49,即∠A≈11°..sin2nd F0?5168=,2nd Ftan0?918=,2nd F°′ ″cos0?3765=2nd F,知2-讲 计算器直接计算出的角的单位是度,而不是
度、分、秒,因此若要得到用度、分、秒表示的
角度,可以借助 和 键.2nd F°′ ″已知下列锐角三角函数值,用计算器求其相应
锐角的度数:
(1)sin A= 0. 627 5,sin B= 0.054 7;
(2)cos A= 0. 625 2, cos B= 0. 165 9; (3)tan A= 4. 842 5,tan B= 0.881 6.知2-练2 已知sin α= ,求α,若用科学计算器计算且
结果以度、分、秒为单位,最后应按键( )
A.AC/ON B.
C.MODE D.
已知α为锐角,且tan α=3.387,下列各值中与α
最接近的是 ( )
A.73°33′ B.73°27′
C.16°27′ D.16°21′知2-练2nd F°′ ″3知识点用计算器探究三角函数的性质知3-讲1.用计算器求下列各组锐角的三角函数值,从中你
能得出什么猜想?
(1)sin83°,cos7°;
(2)sin56°,cos34°;
(3) sin27°36′ , cos62°24′..知3-讲2.用计算器求下列各组锐角的三角函数值,从中你能
得出什么猜想?
(1)sin13°, sin25°,sin36°,sin44° , sin57°,
sin68°, sin79°17′ , sin83°27′53″;
(2)cos17°34′,cos34°27′53″ , cos53°18′ ,
cos69°57′ 3″, cos77°17′ , cos88°17′25″;
(3)tan27°34′ , tan43°57′28″ , tan52°18′15″ ,
tan67°, tan78°17′ , tan85°24′ ..知3-讲.1. 猜想:sin = cos(90°- ).
2. (1)猜想:对于锐角A,它的正弦函数 (sinA)的
函数值随自变量锐角A的增大而增大,且
sinA必满足 0 < sinA<1.
(2)猜想:对于锐角A,它的余弦函数(cosA)的
函数值随锐角A的增大而减小,且cosA必满
足0 < cosA < 1.
(3)猜想:对于锐角A,它的正切函数(tanA)
的函数值随锐角A的增大而增大 , 且tanA
满足0 < tanA.知3-讲(1)sin = cos(90°- ).
(2)对于锐角A,它的正弦函数 (sinA)的函数值随自变
量锐角A的增大而增大,且sinA必满足0 < sinA<1.
(3)对于锐角A,它的余弦函数(cosA)的函数值随锐
角A的增大而减小,且cosA必满足0 < cosA < 1.
(4)对于锐角A,它的正切函数(tanA)的函数值随锐
角A的增大而增大 , 且tanA 满足0 < tanA.知3-讲.例3 已知α+β=90°.探究:
(1)sin α与cos β的关系;
(2)tan α与tan β的关系.
导引:根据α和β互余,可以将α和β放入同一个直角
三角形中,利用锐角三角函数的定义去探究
互为余角的两角的三角函数关系.知3-讲.解:如图,在Rt△ABC中,∠C=90°,∠A=α,
∠B=β.
令∠A,∠B,∠C所对的边分别是a,b,c.
(1)∵sin α= , cos β= ,
∴sin α=cos β.
(2)∵tan α= , tan β= ,
∴tan α·tan β=1.知3-讲互为余角的两角的三角函数间的关系:
(1)任意锐角的正弦值等于它的余角的余弦值,即
sin α=cos (90°-α)或cos α=sin (90°-α);
(2)任意锐角的正切值与它的余角的正切值互为倒
数,即tan α·tan (90°-α)=1. 在Rt△ABC中,已知∠C=90°,sin A= ,
则cos B的值等于( )
A. B. C. D.
已知α为锐角,若tan (90°-α)= ,则
tan α=________.知3-练3 在Rt△ABC中,∠C=90°,下列各式中正确
的是( )
A.sin A=sin B B.tan A=tan B
C.sin A=cos B D.cos A=cos B知3-练1.利用计算器可求锐角的三角函数值,按键顺序为:
先按 键或 键或 键,再按角度值,
最后按 键就可求出相应的三角函数值.
2.已知锐角三角函数值也可求相应的锐角,按键顺
序为:先按 键,再按 键或 键或
键,然后输入三角函数值,最后按 键
就可求出相应角度.sinsincoscostantan2nd F==
函数值1课堂讲解用计算器求已知锐角的三角函数值
用计算器求已知三角函数值的对应角
用计算器探究三角函数的性质2课时流程逐点
导讲练课堂小结作业提升 要测量教学楼的高度,小英身高1.6m.她在距离教学楼30m处测得仰角为25°,你能借助计算器估算出教学楼的高度吗?(精确到0.1m)1知识点用计算器求已知锐角的三角函数值 通过上面的学习,我们知道,当锐角A是 30°,45°或60°等特殊角时,可以求得这些
特殊角的 锐角三角函数值;如果锐角A不是这
些特殊角, 怎样得到它的锐角三角函数值呢?知1-讲知1-讲 我们可以借助计算器求锐角三角函数值.
例如求sin18°,利用计算器的 键,并输入角
度值18,得到结果sin18°=0.309 016 994.
又如求tan30°36′,利用 键,并输入角的度、
分值(可以使用 键),就可以得到结果
0.591 398 351.
因为30°36′=30.6°,所以也可以利用 键,并
输入角度值30.6,同样得到结果0.591 398 351.sintan°′ ″tan知1-讲利用计算器求锐角三角函数值:
1. 当锐角的大小以度为单位时,可先按 , ,
键,然后输入角度值(可以是整数,也可以是
小数),最后按 键,就可以在显示屏上显示出
结果;
2. 当锐角的大小以度、分、秒为单位时要借助
键计算,按键顺序是: (或 、 )、度数、
、分数、 、秒数、 、 .sincostan=°′ ″sincostan°′ ″°′ ″°′ ″= 例1 用计算器求sin 16°,cos 42°,tan 85°,
sin 72°38′25″的值.知1-讲解:如下表:sintansin164cos285252738====°′ ″°′ ″°′ ″知1-讲 要注意不同型号的计算器的操
作步骤可能有所不同.1 用计算器求下列锐角三角函数值:
(1)sin 20°,cos 70°;
sin 35°, cos 55°;
sin15°32′,cos74°28′;
(2)tan 3° 8',tan 80° 25′43".知1-练 分析第1(1)题的结果,你能得出什么猜想?你能说明自己的猜想吗?知1-练(2016·烟台)如图,是我们数学课上采用的科学计
算器面板,利用该型号计算器计算 cos 55°,
按键顺序正确的是( )
A.
B.
C.
D.
利用计算器求sin 30°时,依次按键
,则计算器上显示的结果是( )
A.0.5 B.0.707 C.0.866 D.1sin30°′ ″=cos255×=cos2550=cos255=cos255=2知识点用计算器求已知三角函数值的对应角知2-讲 如果已知锐角三角函数值,也可以使用计算
器求出相应锐角的度数.
例如,已知sin A=0. 501 8,用计算器求锐角A
可以按照下面方法操作:
依次按键 ,然后输入函数值
0.501 8,得到∠A=30.119 158 67° (这说明锐角A
精确到1°的结果为30°)..sin2nd F知2-讲 还可以利用 键,进一步得
到∠A=30 °07′08.97″(这说明锐角A精确到
1′的结果为30°7′,精确到 1"的结果为30°
7′9″)..2nd F°′ ″知2-讲已知锐角三角函数值求锐角的度数:
如果是特殊角(30°, 45°,60°)的三角函
数值,可直接写出其相应的角的度数;若不是特殊
角的三角函数值,应利用计算器求角的度数.求角
的度数要先按 键,将 、 、 转化
成它们的第二功能键;当三角函数值为分数时,应
先化成小数.2nd Fsincostan知2-讲例2 已知下列锐角三角函数值,用计算器求
其相应的锐角:
(1)sin A=0.516 8(结果精确到0.01°);
(2)cos A=0.675 3(结果精确到1″);
(3)tan A=0.189(结果精确到1°)..导引:已知锐角三角函数值,利用计算器求锐
角的度数时要注意先按 键.2nd F知2-讲解:(1)依次按键:
显示结果为:31.117 845 56,即∠A≈31.12°.
(2)依次按键:
显示结果为:47°31′21.18″,
即 ∠A≈47°31′21″.
(3)依次按键:
显示结果为:10.702 657 49,即∠A≈11°..sin2nd F0?5168=,2nd Ftan0?918=,2nd F°′ ″cos0?3765=2nd F,知2-讲 计算器直接计算出的角的单位是度,而不是
度、分、秒,因此若要得到用度、分、秒表示的
角度,可以借助 和 键.2nd F°′ ″已知下列锐角三角函数值,用计算器求其相应
锐角的度数:
(1)sin A= 0. 627 5,sin B= 0.054 7;
(2)cos A= 0. 625 2, cos B= 0. 165 9; (3)tan A= 4. 842 5,tan B= 0.881 6.知2-练2 已知sin α= ,求α,若用科学计算器计算且
结果以度、分、秒为单位,最后应按键( )
A.AC/ON B.
C.MODE D.
已知α为锐角,且tan α=3.387,下列各值中与α
最接近的是 ( )
A.73°33′ B.73°27′
C.16°27′ D.16°21′知2-练2nd F°′ ″3知识点用计算器探究三角函数的性质知3-讲1.用计算器求下列各组锐角的三角函数值,从中你
能得出什么猜想?
(1)sin83°,cos7°;
(2)sin56°,cos34°;
(3) sin27°36′ , cos62°24′..知3-讲2.用计算器求下列各组锐角的三角函数值,从中你能
得出什么猜想?
(1)sin13°, sin25°,sin36°,sin44° , sin57°,
sin68°, sin79°17′ , sin83°27′53″;
(2)cos17°34′,cos34°27′53″ , cos53°18′ ,
cos69°57′ 3″, cos77°17′ , cos88°17′25″;
(3)tan27°34′ , tan43°57′28″ , tan52°18′15″ ,
tan67°, tan78°17′ , tan85°24′ ..知3-讲.1. 猜想:sin = cos(90°- ).
2. (1)猜想:对于锐角A,它的正弦函数 (sinA)的
函数值随自变量锐角A的增大而增大,且
sinA必满足 0 < sinA<1.
(2)猜想:对于锐角A,它的余弦函数(cosA)的
函数值随锐角A的增大而减小,且cosA必满
足0 < cosA < 1.
(3)猜想:对于锐角A,它的正切函数(tanA)
的函数值随锐角A的增大而增大 , 且tanA
满足0 < tanA.知3-讲(1)sin = cos(90°- ).
(2)对于锐角A,它的正弦函数 (sinA)的函数值随自变
量锐角A的增大而增大,且sinA必满足0 < sinA<1.
(3)对于锐角A,它的余弦函数(cosA)的函数值随锐
角A的增大而减小,且cosA必满足0 < cosA < 1.
(4)对于锐角A,它的正切函数(tanA)的函数值随锐
角A的增大而增大 , 且tanA 满足0 < tanA.知3-讲.例3 已知α+β=90°.探究:
(1)sin α与cos β的关系;
(2)tan α与tan β的关系.
导引:根据α和β互余,可以将α和β放入同一个直角
三角形中,利用锐角三角函数的定义去探究
互为余角的两角的三角函数关系.知3-讲.解:如图,在Rt△ABC中,∠C=90°,∠A=α,
∠B=β.
令∠A,∠B,∠C所对的边分别是a,b,c.
(1)∵sin α= , cos β= ,
∴sin α=cos β.
(2)∵tan α= , tan β= ,
∴tan α·tan β=1.知3-讲互为余角的两角的三角函数间的关系:
(1)任意锐角的正弦值等于它的余角的余弦值,即
sin α=cos (90°-α)或cos α=sin (90°-α);
(2)任意锐角的正切值与它的余角的正切值互为倒
数,即tan α·tan (90°-α)=1. 在Rt△ABC中,已知∠C=90°,sin A= ,
则cos B的值等于( )
A. B. C. D.
已知α为锐角,若tan (90°-α)= ,则
tan α=________.知3-练3 在Rt△ABC中,∠C=90°,下列各式中正确
的是( )
A.sin A=sin B B.tan A=tan B
C.sin A=cos B D.cos A=cos B知3-练1.利用计算器可求锐角的三角函数值,按键顺序为:
先按 键或 键或 键,再按角度值,
最后按 键就可求出相应的三角函数值.
2.已知锐角三角函数值也可求相应的锐角,按键顺
序为:先按 键,再按 键或 键或
键,然后输入三角函数值,最后按 键
就可求出相应角度.sinsincoscostantan2nd F==
