28.2.2 解直角三角形的八种类型课件
文档属性
| 名称 | 28.2.2 解直角三角形的八种类型课件 |  | |
| 格式 | zip | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 08:37:36 | ||
图片预览








文档简介
课件20张PPT。第二十八章 锐角三角函数28.2 解直角三角形及其应用第2课时 解直角三角形
的八种类型 名师点金解直角三角形时,首先要分析直角三角形中的已知元素,根据已知元素利用勾股定理、边角关系、斜边上的中线性质,30°角所对直角边的性质进行求解.求边的长度时,一般要选择题目中的原始数据,尽量避免用中间所得的结果参与计算.1类型已知两边解直角三角形1.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)a= ,b= ;
(2)a= ,b=10.解:(1) tan A= = ,
∴∠A=60°,
∴∠B=30°. c=2b=12 .
(2) tan A= = ,
∴∠A=60°,
∴∠B=30°. c=2b=20.2已知一边和一个锐角解直角三角形类型2.在△ABC中,∠C=90°,∠A=60°.
(1)若c=10,求a,b的值;
(2)若a=4,求b及∠B的值.解: (1) a=c?sinA=10?sin 60°=5 ,
b=c?cos A=10?cos 60°=5;(2)
∠B=90°-∠A=30°.3已知一边和一锐角的三角函数值解直角三角形类型3. (中考?上海)如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD交CD的延长线于点E.已知AC=15,cosA= .
(1)求线段CD的长;
(2)求sin∠DBE的值.解: (1)在Rt△ACB中,cos A= ,
即
(2)由(1)可得AD=BD=CD= ,
∴ .
设DE=x,EB=y,则
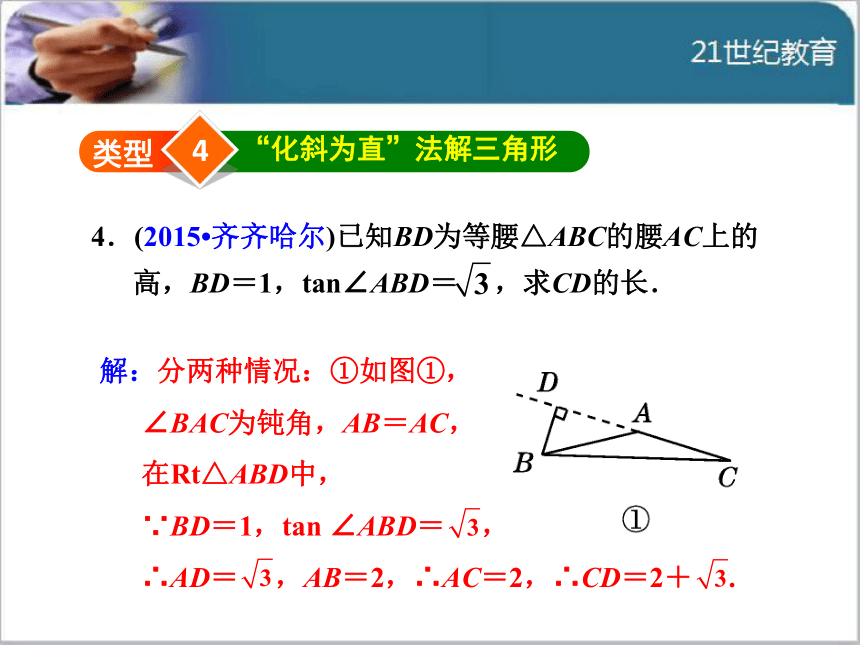
∴sin ∠DBE=4“化斜为直”法解三角形4.(2015?齐齐哈尔)已知BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD= ,求CD的长.类型解:分两种情况:①如图①,
∠BAC为钝角,AB=AC,
在Rt△ABD中,
∵BD=1,tan ∠ABD= ,
∴AD= ,AB=2,∴AC=2,∴CD=2+ .② 如图②,∠BAC为锐角,AB=AC,在Rt△ABD中,∵BD=1,tan ∠ABD=3,
∴AD= ,AB=2,∴AC=2,
∴CD=2- .
综上所述,CD的长为2+ 或2- .5“参数法”解直角三角形5.如图,已知△ABC是等腰直角三角形,∠ABC=90°,AB=10,D为△ABC外一点,连接AD,BD,过D作DH⊥AB,垂足为H,交AC于E.
(1)若△ABD是等边三角形,
求DE的长;
(2)若BD=AB,且tan∠HDB
= ,求DE的长.类型 (1)∵△ABD是等边三角形,AB=10.
∴∠ADB=60°,AD=AB=10.
∵DH⊥AB,∴AH= AB=5.
∴
∵△ABC是等腰直角三角形,∴∠CAB=45°.
∴∠AEH=45°,∴EH=AH=5.
∴DE=DH-EH=解:(2) ∵DH⊥AB且tan ∠HDB= .
∴可设BH=3k,则DH=4k,DB=5k(k>0).
∵BD=AB=10,∴5k=10,解得k=2.
∴DH=8,BH=6,AH=4.
又∵EH=AH=4,∴DE=DH-EH=4.6“等角代换法”解三角形6.如图,在△ABC中,AD,CE是高,AB=4,AC=5,BC=6,求cos∠DEB.类型思路导引:
因为相对于∠DEB没有已知条件,它又不在直角三角形中,所以可以选择一个与∠DEB相等的角来转换,又易证得△DBE∽△ABC,
所以有∠ACB=∠DEB.解:∵AD,CE是△ABC的高,
∴∠ADB=∠CEB=90°.
∵∠B=∠B,∴△ADB∽△CEB,
∴
∵∠B=∠B,∴△DBE∽△ABC.
∴∠ACB=∠DEB.
设CD=x,则DB=6-x.
在Rt△ABD中,AD2=AB2-DB2,
在Rt△ACD中,AD2=AC2-CD2,∴AB2-DB2=AC2-CD2.
∵AB=4,AC=5,
∴42-(6-x)2=52-x2,解得x= .
∴在Rt△ACD中,cos ∠ACB=
∵∠ACB=∠DEB,
∴cos ∠DEB= .
7“定义法”解直角三角形7. 如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.
(1)求证:CD∥BF;
(2)若⊙O的半径为5,cos∠BAD
= ,求线段AD的长.类型(1) 证明:∵BF是⊙O的切线,AB是⊙O的直径,
∴BF⊥AB,
∵CD⊥AB,
∴CD∥BF.
(2) 解:如图,连接BD,
∵AB是直径,∴∠ADB=90°,
∵⊙O的半径是5,∴AB=10,
∵cos ∠BAD= ,
∴AD=AB?cos ∠BAD=10× =8.8“等比代换法”解直角三角形8.如图,在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B,A,与反比例函数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=4,
OE=2.
(1)求该反比例函数的解析式;
(2)求直线AB对应的函数解析式.类型解:(1) ∵tan ∠ABO=
∴CE=3,AO=2,
∴A(0,2),B(4,0),C(-2,3),
可求得反比例函数的解析式为y= .
(2) 设直线AB对应的函数解析式为y=kx+b,
将A(0,2),B(4,0)的坐标代入y=kx+b
可得b=2,k=- ,
所以解析式为y=- +2.
的八种类型 名师点金解直角三角形时,首先要分析直角三角形中的已知元素,根据已知元素利用勾股定理、边角关系、斜边上的中线性质,30°角所对直角边的性质进行求解.求边的长度时,一般要选择题目中的原始数据,尽量避免用中间所得的结果参与计算.1类型已知两边解直角三角形1.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)a= ,b= ;
(2)a= ,b=10.解:(1) tan A= = ,
∴∠A=60°,
∴∠B=30°. c=2b=12 .
(2) tan A= = ,
∴∠A=60°,
∴∠B=30°. c=2b=20.2已知一边和一个锐角解直角三角形类型2.在△ABC中,∠C=90°,∠A=60°.
(1)若c=10,求a,b的值;
(2)若a=4,求b及∠B的值.解: (1) a=c?sinA=10?sin 60°=5 ,
b=c?cos A=10?cos 60°=5;(2)
∠B=90°-∠A=30°.3已知一边和一锐角的三角函数值解直角三角形类型3. (中考?上海)如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD交CD的延长线于点E.已知AC=15,cosA= .
(1)求线段CD的长;
(2)求sin∠DBE的值.解: (1)在Rt△ACB中,cos A= ,
即
(2)由(1)可得AD=BD=CD= ,
∴ .
设DE=x,EB=y,则
∴sin ∠DBE=4“化斜为直”法解三角形4.(2015?齐齐哈尔)已知BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD= ,求CD的长.类型解:分两种情况:①如图①,
∠BAC为钝角,AB=AC,
在Rt△ABD中,
∵BD=1,tan ∠ABD= ,
∴AD= ,AB=2,∴AC=2,∴CD=2+ .② 如图②,∠BAC为锐角,AB=AC,在Rt△ABD中,∵BD=1,tan ∠ABD=3,
∴AD= ,AB=2,∴AC=2,
∴CD=2- .
综上所述,CD的长为2+ 或2- .5“参数法”解直角三角形5.如图,已知△ABC是等腰直角三角形,∠ABC=90°,AB=10,D为△ABC外一点,连接AD,BD,过D作DH⊥AB,垂足为H,交AC于E.
(1)若△ABD是等边三角形,
求DE的长;
(2)若BD=AB,且tan∠HDB
= ,求DE的长.类型 (1)∵△ABD是等边三角形,AB=10.
∴∠ADB=60°,AD=AB=10.
∵DH⊥AB,∴AH= AB=5.
∴
∵△ABC是等腰直角三角形,∴∠CAB=45°.
∴∠AEH=45°,∴EH=AH=5.
∴DE=DH-EH=解:(2) ∵DH⊥AB且tan ∠HDB= .
∴可设BH=3k,则DH=4k,DB=5k(k>0).
∵BD=AB=10,∴5k=10,解得k=2.
∴DH=8,BH=6,AH=4.
又∵EH=AH=4,∴DE=DH-EH=4.6“等角代换法”解三角形6.如图,在△ABC中,AD,CE是高,AB=4,AC=5,BC=6,求cos∠DEB.类型思路导引:
因为相对于∠DEB没有已知条件,它又不在直角三角形中,所以可以选择一个与∠DEB相等的角来转换,又易证得△DBE∽△ABC,
所以有∠ACB=∠DEB.解:∵AD,CE是△ABC的高,
∴∠ADB=∠CEB=90°.
∵∠B=∠B,∴△ADB∽△CEB,
∴
∵∠B=∠B,∴△DBE∽△ABC.
∴∠ACB=∠DEB.
设CD=x,则DB=6-x.
在Rt△ABD中,AD2=AB2-DB2,
在Rt△ACD中,AD2=AC2-CD2,∴AB2-DB2=AC2-CD2.
∵AB=4,AC=5,
∴42-(6-x)2=52-x2,解得x= .
∴在Rt△ACD中,cos ∠ACB=
∵∠ACB=∠DEB,
∴cos ∠DEB= .
7“定义法”解直角三角形7. 如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.
(1)求证:CD∥BF;
(2)若⊙O的半径为5,cos∠BAD
= ,求线段AD的长.类型(1) 证明:∵BF是⊙O的切线,AB是⊙O的直径,
∴BF⊥AB,
∵CD⊥AB,
∴CD∥BF.
(2) 解:如图,连接BD,
∵AB是直径,∴∠ADB=90°,
∵⊙O的半径是5,∴AB=10,
∵cos ∠BAD= ,
∴AD=AB?cos ∠BAD=10× =8.8“等比代换法”解直角三角形8.如图,在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B,A,与反比例函数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=4,
OE=2.
(1)求该反比例函数的解析式;
(2)求直线AB对应的函数解析式.类型解:(1) ∵tan ∠ABO=
∴CE=3,AO=2,
∴A(0,2),B(4,0),C(-2,3),
可求得反比例函数的解析式为y= .
(2) 设直线AB对应的函数解析式为y=kx+b,
将A(0,2),B(4,0)的坐标代入y=kx+b
可得b=2,k=- ,
所以解析式为y=- +2.
