28.2.4 用解直角三角形解视角问题课件
文档属性
| 名称 | 28.2.4 用解直角三角形解视角问题课件 |  | |
| 格式 | zip | ||
| 文件大小 | 553.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 08:38:48 | ||
图片预览






文档简介
课件18张PPT。第二十八章 锐角三角函数28.2 解直角三角形及其应用第4课时 用解直角三角形
解视角问题1课堂讲解仰角的应用
俯角的应用2课时流程逐点
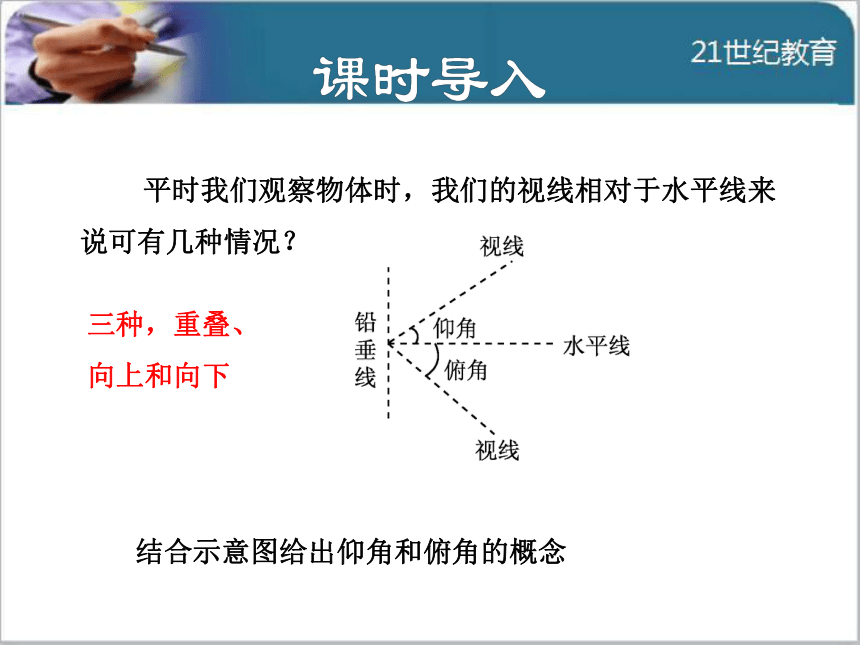
导讲练课堂小结作业提升 平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
结合示意图给出仰角和俯角的概念三种,重叠、
向上和向下1知识点仰角的应用 例1 2012年6月18日,“神舟”九号载人航天飞船与“天
宫”一号目标 飞行器成功实现交会对接.“神舟”
九号与“天宫”一号的组合体在离地球表 面343 km
的圆形轨道上运行,如图,知1-讲知1-讲当组合体运行到地球表面P点 的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P 点的距离是多少(地球半径约为6 400 km, π取3. 142,结果取整数)?知1-讲分析:从组合体中能直接看到的地球表面最 远点,
是视线与地球相切时的切点. 如图,本例可以抽
象为以地球中心为 圆心、地球半径为半径的
⊙O的有关问题:其中点F是组合体的位置,
FQ是⊙O的切线,切点Q 是从组合体中观测
地球时的最远点, 的长就是 地球表面上
P,Q两点间的距离.为计算 的长需先求
出∠ POQ (即α)的度数.知1-讲设∠ POQ= α,在图中,FQ是⊙O 的切线,
△FOQ是直角三角形.
∴α≈18.36°.
∴
解: 由此可知,当组合体在P点正上方时,从中观测
地球表面时的最远点距离P点约2 051 km.知1-讲利用解直角三角形解决实物模型问题的一般过程是:
①将实际问题抽象为数学问题(画出平面图形,构造出直
角三角形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系
去解直角三角形,得到数学问题的答案,再转化得到
实际问题的答案.1 如图,建筑物BC上有一旗杆AB,从与BC相距40 m
的D处观测旗杆顶部A 的仰角为50°,观测旗杆底部B的仰角为45°,求旗杆的高度(结果保留小数点后一位).
知1-练2 (2015·长沙)如图,为测量一棵与地面垂直的树OA
的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米知1-练3 (2015·聊城)湖南路大桥于今年5月1日竣工,为徒骇河景
区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈
0.749,tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米知1-练2知识点俯角的应用知2-讲例2 热气球的探测器显示,从热气球看一栋楼顶部
的仰角为30°,看这栋楼底部的俯角为60°,
热气球与楼的水平距离为120 m,这栋楼有多高
(结果取整数)?知2-讲分析:我们知道,在视线与水平线所成的角中, 视
线在水平线上方的是仰角,视线在水平线下
方的是俯角.因此,在图中, α =30°, β =
60°.在 Rt△ABD 中, α = 30°,AD = 120,
所以可以利用解直角三角形的知识求出BD;
类似地可以求出CD,进而求出BC.
知2-讲 如图,α =30°, β =60°,AD=120.
∵
∴ BD=AD·tan α=120×tan30°
CD=AD·tan β=120×tan 60°
∴BC=BD+CD=
因此,这栋楼高约为277 m.解:知2-讲 解决与俯角和仰角有关的实际问题,必须先根据
视角(仰角、俯角)的意义画出水平线找准视角,建立数
学模型,然后构造直角三角形,利用解直角三角形的
知识解决要求的问题.1 如图,某飞机于空中A处探测到目标C,此时飞行高度AC = 1 200 m,从飞机上 看地平面指挥台B的俯角α = 16°31′.求飞机A与指挥台B的距离(结果取整数).
知2-练知2-练2 (2015·哈尔滨)如图,某飞机在空中A处探测到它的
正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则A处与指挥台B的距离为( )
A.1200 m
B.1200 m
C.1200 m
D.2400 m
?解含有仰角、俯角问题的方法
(1)仰角和俯角是指视线相对于水平线而言的,不同位置的
仰角和俯角是不同的,可巧记为“上仰下俯”.在测量物
体的高度时,要善于将实际问题抽象为数学问题.
(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯
角)和另一边,利用解直角三角形的知识就可以求出物体
的高度.
(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实
际问题中的数量关系归结到直角三角形中来求解.
解视角问题1课堂讲解仰角的应用
俯角的应用2课时流程逐点
导讲练课堂小结作业提升 平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
结合示意图给出仰角和俯角的概念三种,重叠、
向上和向下1知识点仰角的应用 例1 2012年6月18日,“神舟”九号载人航天飞船与“天
宫”一号目标 飞行器成功实现交会对接.“神舟”
九号与“天宫”一号的组合体在离地球表 面343 km
的圆形轨道上运行,如图,知1-讲知1-讲当组合体运行到地球表面P点 的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P 点的距离是多少(地球半径约为6 400 km, π取3. 142,结果取整数)?知1-讲分析:从组合体中能直接看到的地球表面最 远点,
是视线与地球相切时的切点. 如图,本例可以抽
象为以地球中心为 圆心、地球半径为半径的
⊙O的有关问题:其中点F是组合体的位置,
FQ是⊙O的切线,切点Q 是从组合体中观测
地球时的最远点, 的长就是 地球表面上
P,Q两点间的距离.为计算 的长需先求
出∠ POQ (即α)的度数.知1-讲设∠ POQ= α,在图中,FQ是⊙O 的切线,
△FOQ是直角三角形.
∴α≈18.36°.
∴
解: 由此可知,当组合体在P点正上方时,从中观测
地球表面时的最远点距离P点约2 051 km.知1-讲利用解直角三角形解决实物模型问题的一般过程是:
①将实际问题抽象为数学问题(画出平面图形,构造出直
角三角形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系
去解直角三角形,得到数学问题的答案,再转化得到
实际问题的答案.1 如图,建筑物BC上有一旗杆AB,从与BC相距40 m
的D处观测旗杆顶部A 的仰角为50°,观测旗杆底部B的仰角为45°,求旗杆的高度(结果保留小数点后一位).
知1-练2 (2015·长沙)如图,为测量一棵与地面垂直的树OA
的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米知1-练3 (2015·聊城)湖南路大桥于今年5月1日竣工,为徒骇河景
区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈
0.749,tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米知1-练2知识点俯角的应用知2-讲例2 热气球的探测器显示,从热气球看一栋楼顶部
的仰角为30°,看这栋楼底部的俯角为60°,
热气球与楼的水平距离为120 m,这栋楼有多高
(结果取整数)?知2-讲分析:我们知道,在视线与水平线所成的角中, 视
线在水平线上方的是仰角,视线在水平线下
方的是俯角.因此,在图中, α =30°, β =
60°.在 Rt△ABD 中, α = 30°,AD = 120,
所以可以利用解直角三角形的知识求出BD;
类似地可以求出CD,进而求出BC.
知2-讲 如图,α =30°, β =60°,AD=120.
∵
∴ BD=AD·tan α=120×tan30°
CD=AD·tan β=120×tan 60°
∴BC=BD+CD=
因此,这栋楼高约为277 m.解:知2-讲 解决与俯角和仰角有关的实际问题,必须先根据
视角(仰角、俯角)的意义画出水平线找准视角,建立数
学模型,然后构造直角三角形,利用解直角三角形的
知识解决要求的问题.1 如图,某飞机于空中A处探测到目标C,此时飞行高度AC = 1 200 m,从飞机上 看地平面指挥台B的俯角α = 16°31′.求飞机A与指挥台B的距离(结果取整数).
知2-练知2-练2 (2015·哈尔滨)如图,某飞机在空中A处探测到它的
正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则A处与指挥台B的距离为( )
A.1200 m
B.1200 m
C.1200 m
D.2400 m
?解含有仰角、俯角问题的方法
(1)仰角和俯角是指视线相对于水平线而言的,不同位置的
仰角和俯角是不同的,可巧记为“上仰下俯”.在测量物
体的高度时,要善于将实际问题抽象为数学问题.
(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯
角)和另一边,利用解直角三角形的知识就可以求出物体
的高度.
(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实
际问题中的数量关系归结到直角三角形中来求解.
