第01周 1.1等腰三角形--1.2直角三角形同步测试
文档属性
| 名称 | 第01周 1.1等腰三角形--1.2直角三角形同步测试 |  | |
| 格式 | zip | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 18:33:12 | ||
图片预览

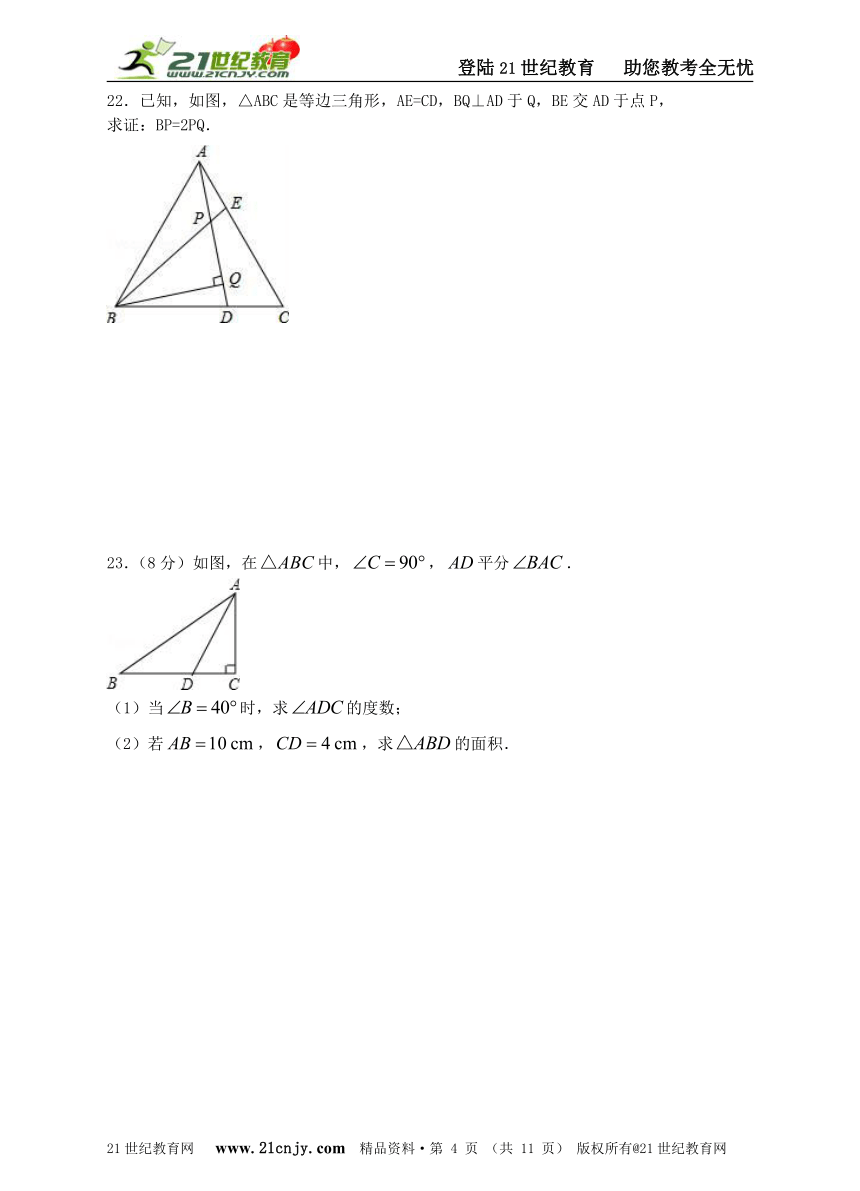
文档简介
【新北师大版八年级数学(下)周周测】
第 1周测试卷
(测试范围:1.1等腰三角形——1.2直角三角形)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分,共30分)
1.等腰三角形的两边长分别是4和8,则这个等腰三角形的周长为( )
A.16 B.18 C.20 D.16或20
2.已知△ABC为等边三角形,则∠A的度数是( )
A.30° B.45° C.60° D.90°
3.已知等腰三角形的腰长为2,底边长不可能的是( ).
A.1 B.2 C.3 D.4
4.如图,在△ABC中,AB=AC,∠B=40o,D为BC上一点,DE∥AC交AB于E,则∠BED的度数为( )21·cn·jy·com
A.140o B.80o C.100o D.70o
5.等腰三角形一腰上的高与另一要的夹角为300,则顶角度数为( )
A.300 B.600 C.900 D.1200或600
6.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( ).21教育网
A.2cm B.3cm C.4cm D.5cm
7.下列判定直角三角形全等的方法,不正确的是( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两锐角相等
8.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为( )21教育名师原创作品
A.3 B.3.5 C.4 D.4.5
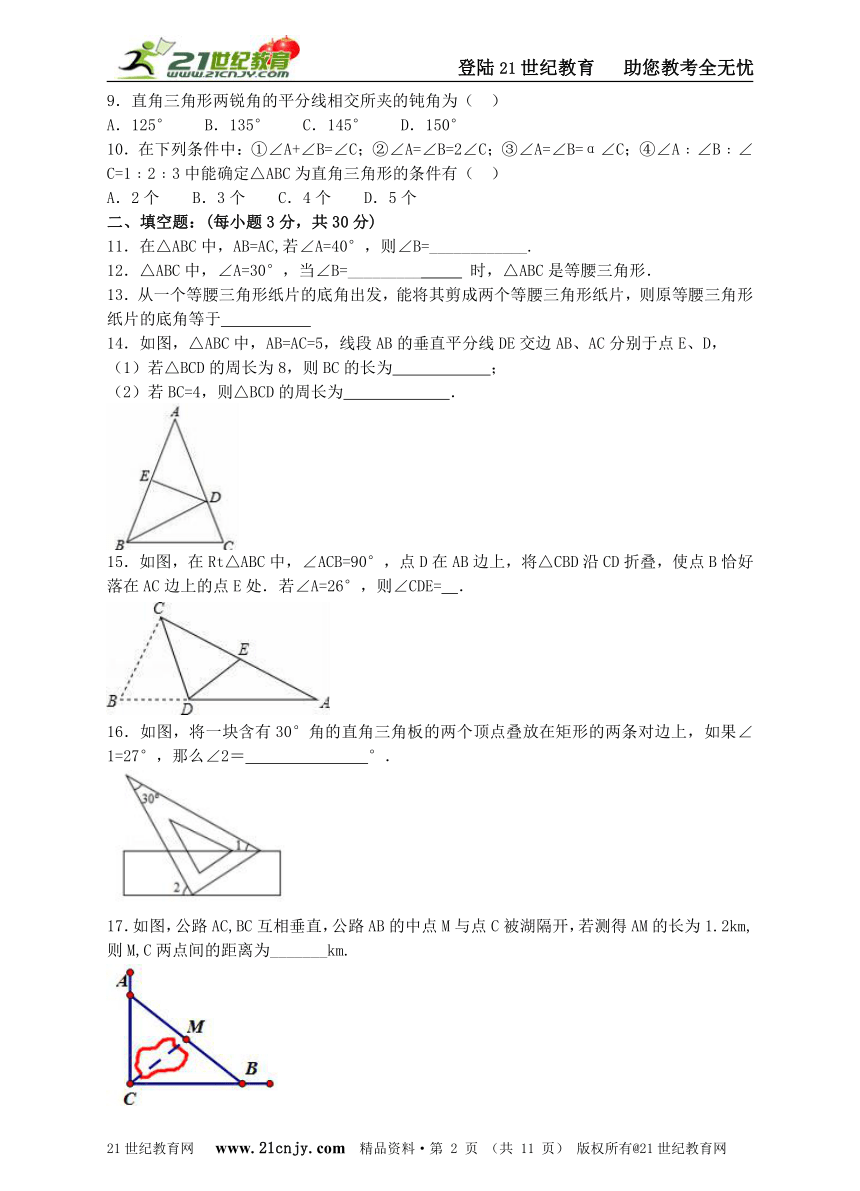
9.直角三角形两锐角的平分线相交所夹的钝角为( )
A.125° B.135° C.145° D.150°
10.在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A=∠B=α∠C;④∠A﹕∠B﹕∠C=1﹕2﹕3中能确定△ABC为直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
二、填空题:(每小题3分,共30分)
11.在△ABC中,AB=AC,若∠A=40°,则∠B=____________.
12.△ABC中,∠A=30°,当∠B=_________ 时,△ABC是等腰三角形.
13.从一个等腰三角形纸片的底角出发,能将其剪成两个等腰三角形纸片,则原等腰三角形纸片的底角等于
14.如图,△ABC中,AB=AC=5,线段AB的垂直平分线DE交边AB、AC分别于点E、D,
(1)若△BCD的周长为8,则BC的长为 ;
(2)若BC=4,则△BCD的周长为 .
15.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE= .
16.如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=27°,那么∠2= °.
17.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为_______km.
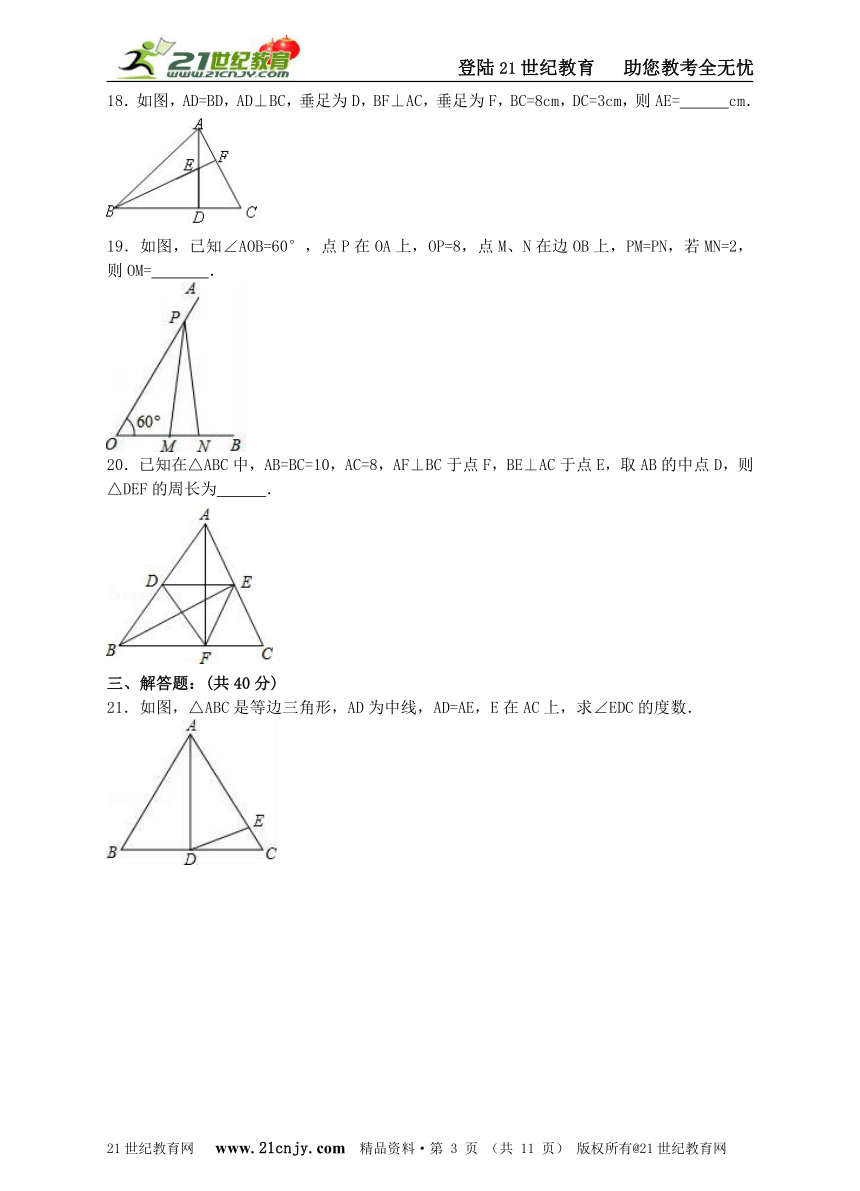
18.如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=8cm,DC=3cm,则AE= cm.
19.如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM= .
20.已知在△ABC中,AB=BC=10,AC=8,AF⊥BC于点F,BE⊥AC于点E,取AB的中点D,则△DEF的周长为 .
三、解答题:(共40分)
21.如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
22.已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
求证:BP=2PQ.
23.(8分)如图,在中,,平分.
(1)当时,求的度数;
(2)若,,求的面积.
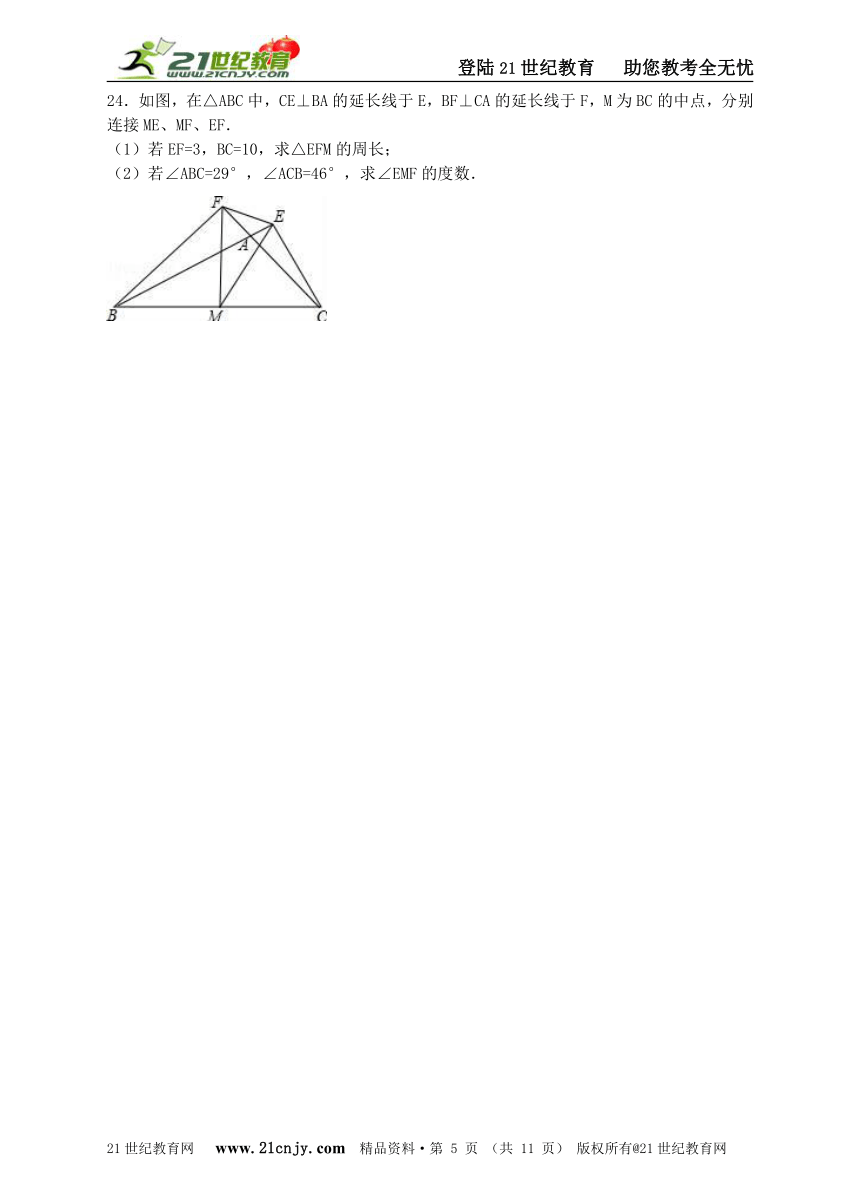
24.如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.21cnjy.com
(1)若EF=3,BC=10,求△EFM的周长;
(2)若∠ABC=29°,∠ACB=46°,求∠EMF的度数.
参考答案
1.C
【解析】
试题分析:如果4为腰长,8为底时则无法构成三角形;当8为腰长,4为底时,则周长=8+8+4=20.
2.C
【解析】
试题分析:等边三角形性质:
1三边相等
2三个角都相等
3三个角都等于60°
4高线、腰、底边中线三线合一.
三角形为等边三角形,等边三角形三边相等,三个角也相等.
解:已知三角形为等边三角形,所以∠A=∠B=∠C==60°.
故选C.
3.D.
【解析】
试题分析:根据等腰三角形的性质与三角形三边关系,可知等腰三角形腰长是2,∴2+2=4∴底边不可能是4.www.21-cn-jy.com
故选:D.
4.C.
【解析】
试题分析:∵AB=AC,∴∠C=∠B=40°,∴∠A=180°﹣∠B﹣∠C=180°﹣40°﹣40°=100°,∵DE∥AC,∴∠BED=∠A=100°.故选C.【来源:21·世纪·教育·网】
5.D
【解析】
试题分析:分两种情况,(1)此等腰三角形为锐角三角形时,顶角为600 ;(2)此等腰三角形为钝角三角形时,顶角为1200 ,故选:D.21·世纪*教育网
6.B.
【解析】
试题分析:由角平分线的性质可得DE=EC,则AE+DE=AC=3cm.
故选:B.
7.D
【解析】
试题分析:A可利用SAS来判定全等,故正确;B可利用AAS来判定全等,故正确;C可利用HL判定全等,故正确;D面积相等不一定退出两直角三角形全等,没有相关的判定方法,故不正确.【来源:21cnj*y.co*m】
故选D
8.A
【解析】
试题分析:根据∠ACB=90°,∠ABC=60°,BD平分∠ABC可得:BD=AD=6,根据直角三角形斜边上的中线等于斜边的一半得出CP=3.【出处:21教育名师】
9.B
【解析】
试题分析:作出图形,根据直角三角形两锐角互余可得∠BAC+∠ABC=90°,再根据角平分线的定义可得∠OAB+∠OBA=45°,然后根据三角形的内角和定理列式计算即可得解.
解:如图,∵∠C=90°,
∴∠BAC+∠ABC=180°﹣90°=90°,
∵AD、BE分别是∠BAC和∠ABC的平分线,
∴∠OAB+∠OBA=×90°=45°,
∴∠AOB=180°﹣(∠OAB+∠OBA)=180°﹣45°=135°.
故选B.
10.A
【解析】
试题分析:结合三角形的内角和为180°逐个分析4个条件,可得出①④中∠C=90°,②③能确定△ABC为锐角三角形,从而得出结论.【版权所有:21教育】
解:①∵∠A+∠B=∠C,且∠A+∠B+∠C=180°,
∴∠C+∠C=180°,即∠C=90°,
此时△ABC为直角三角形,①可以;
②∵∠A=∠B=2∠C,且∠A+∠B+∠C=180°,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,∠A=∠B=2∠C=72°,
△ABC为锐角三角形,②不可以;
③∵∠A=∠B=α∠C,且∠A+∠B+∠C=180°,
∴α∠C+α∠C+∠C=180°,
∴∠C=,∠A=∠B=α∠C=,
△ABC为锐角三角形,③不可以;
④∵∠A﹕∠B﹕∠C=1﹕2﹕3,
∴∠A+∠B=∠C,同①,
此时△ABC为直角三角形,④可以;
综上可知:①④能确定△ABC为直角三角形.
故选A.
11.70°.
【解析】
试题分析:由AB=AC,根据等腰三角形的性质得到∠B=∠C=.
12.75°或30°或120°
【解析】
试题分析:当∠A为顶角等于30°时,可得底角∠B=(180°-30°)=75°,△ABC是等腰三角形,当∠A=∠B=30°时,△ABC是等腰三角形,当∠A=∠C=30°时,则∠B=120°,△ABC是等腰三角形,故答案为:75°或30°或120°.21世纪教育网版权所有
13.72°或°
【解析】
试题分析:根据等腰三角形的性质,分两种情况分别求出原等腰三角形的底角度数.其中一个三角形的三个内角度数为:36°、72°、72°,还有一个三角形的三个内角度数为:°、°、°.www-2-1-cnjy-com
14.(1)3;(2)9.
【解析】
试题分析:(1)先根据线段垂直平分线的性质得出AD=BD,再由△BCD的周长为8可得BC=8﹣5=3;2·1·c·n·j·y
(2)根据(1)中,AD=BD可得BD+CD=AC=5.∵BC=4,∴△BCD的周长=5+4=9.
故答案为:(1)3;(2)9.
15.71°.
【解析】
试题分析:∵在Rt△ABC中,∠ACB=90°,∠A=26°,∴∠B=64°,
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠CED=∠B=64°,
∴∠CDE=180°﹣∠ECD﹣∠CED=71°,
故答案为:71°.
16.57°.
【解析】
试题分析:根据∠1可得三角板中的另一个角为60°-27°=33°,则∠2=90°-33°=57°.
17.1.2
【解析】
试题分析:直角三角形斜边上的中线等于斜边的一半,根据这个定理可得:MC=AM=BM=1.2km.
18.2
【解析】
试题分析:根据等腰三角形的性质可得:AD=BD=8-3=5,根据△BDE≌△ADC可得DE=DC=3,则AE=AD-DE=5-3=2cm.2-1-c-n-j-y
19.3
【解析】
试题分析:过P作PC垂直于MN,由等腰三角形三线合一性质得到MC=CN,求出MC的长,在直角三角形OPC中,利用30度角所对的直角边等于斜边的一半求出OC的长,由OC﹣MC求出OM的长即可.21*cnjy*com
过P作PC⊥MN, ∵PM=PN, ∴C为MN中点,即MC=NC=MN=1,
在Rt△OPC中,∠AOB=60°, ∴∠OPC=30°, ∴OC=OP=4, 则OM=OC﹣MC=4﹣1=3,21*cnjy*com
20.14
【解析】
试题分析:根据等腰三角形三线合一的性质可得BE是△ABC的中线,然后根据直角三角形斜边上的中线等于斜边的一半可得DF=AB,EF=AC,然后判断出DE是△ABC的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半可得DE=BC,然后根据三角形的周长公式列式计算即可得解.
解:∵BE⊥AC,
∴BE是△ABC的中线,
∵AF⊥BC,D是AB的中点,
∴DF=AB=×10=5,EF=AC=×8=4,
∵BE是△ABC的中线,D是AB的中点,
∴DE是△ABC的中位线,
∴DE=BC=×10=5,
∴△DEF的周长=5+4+5=14.
故答案为:14.
21.15°
【解析】
试题分析:先根据△ABC是等边三角形,AD为中线可得出AD⊥BC,∠CAD=30°,再由AD=AE可知∠ADE=∠AED,根据三角形内角和定理即可求出∠ADE的度数,故可得出∠EDC的度数.
试题解析:∵△ABC是等边三角形,AD为中线, ∴AD⊥BC,∠CAD=30°, ∵AD=AE,
∴∠ADE=∠AED===75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
22.证明详见解析.
【解析】
试题分析:根据等边三角形的性质可得AB=AC,∠BAE=∠C=60°,再利用“边角边”证明△ABE和△CAD全等,根据全等三角形对应角相等可得∠1=∠2,然后求出∠BPQ=60°,再根据直角三角形两锐角互余求出∠PBQ=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半证明即可.
试题解析:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
AB=AC,∠BAE=∠C=60°,AE=CD,
∴△ABE≌△CAD(SAS),
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
∵BQ⊥AD,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.
23.详见解析
【解析】(1)∵,
∴,(2分)
∵平分,
∴,(3分)
∴.(5分)
(2)过作于,
∵平分,,
∴,(7分)
∴.(9分)
24.(1)13;(2)30°.
【解析】
试题分析:(1)根据直角三角形斜边中线的性质得出EM=FM=BC=5,进而可求得△EFM的周长;
(2)根据直角三角形斜边中线的性质得出EM=BM,FM=MC,根据等腰三角形的性质和三角形内角和定理得出∠EMC=58°,∠FMC=88°,进而可求得∠FME=88°﹣58°=30°.
试题解析:(1)∵CE⊥BA,M为BC的中点,
∴EM=BC=4,
∵BF⊥CA,M为BC的中点,
∴FM=BC=4,
∴△EFM的周长为:EM+FM+EF=5+5+3=13;
(2)∵EM=BC,M为BC的中点,
∴BM=EM,
∴∠EBM=∠BEM=29°,
∴∠EMC=58°,
∵FM=BC,M为BC的中点,
∴FM=MC,
∴∠MFC=∠ACB=46°,
∴∠FMC=88°,
∴∠FME=88°﹣58°=30°.
第 1周测试卷
(测试范围:1.1等腰三角形——1.2直角三角形)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分,共30分)
1.等腰三角形的两边长分别是4和8,则这个等腰三角形的周长为( )
A.16 B.18 C.20 D.16或20
2.已知△ABC为等边三角形,则∠A的度数是( )
A.30° B.45° C.60° D.90°
3.已知等腰三角形的腰长为2,底边长不可能的是( ).
A.1 B.2 C.3 D.4
4.如图,在△ABC中,AB=AC,∠B=40o,D为BC上一点,DE∥AC交AB于E,则∠BED的度数为( )21·cn·jy·com
A.140o B.80o C.100o D.70o
5.等腰三角形一腰上的高与另一要的夹角为300,则顶角度数为( )
A.300 B.600 C.900 D.1200或600
6.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( ).21教育网
A.2cm B.3cm C.4cm D.5cm
7.下列判定直角三角形全等的方法,不正确的是( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两锐角相等
8.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为( )21教育名师原创作品
A.3 B.3.5 C.4 D.4.5
9.直角三角形两锐角的平分线相交所夹的钝角为( )
A.125° B.135° C.145° D.150°
10.在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A=∠B=α∠C;④∠A﹕∠B﹕∠C=1﹕2﹕3中能确定△ABC为直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
二、填空题:(每小题3分,共30分)
11.在△ABC中,AB=AC,若∠A=40°,则∠B=____________.
12.△ABC中,∠A=30°,当∠B=_________ 时,△ABC是等腰三角形.
13.从一个等腰三角形纸片的底角出发,能将其剪成两个等腰三角形纸片,则原等腰三角形纸片的底角等于
14.如图,△ABC中,AB=AC=5,线段AB的垂直平分线DE交边AB、AC分别于点E、D,
(1)若△BCD的周长为8,则BC的长为 ;
(2)若BC=4,则△BCD的周长为 .
15.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE= .
16.如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=27°,那么∠2= °.
17.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为_______km.
18.如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=8cm,DC=3cm,则AE= cm.
19.如图,已知∠AOB=60°,点P在OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则OM= .
20.已知在△ABC中,AB=BC=10,AC=8,AF⊥BC于点F,BE⊥AC于点E,取AB的中点D,则△DEF的周长为 .
三、解答题:(共40分)
21.如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
22.已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
求证:BP=2PQ.
23.(8分)如图,在中,,平分.
(1)当时,求的度数;
(2)若,,求的面积.
24.如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.21cnjy.com
(1)若EF=3,BC=10,求△EFM的周长;
(2)若∠ABC=29°,∠ACB=46°,求∠EMF的度数.
参考答案
1.C
【解析】
试题分析:如果4为腰长,8为底时则无法构成三角形;当8为腰长,4为底时,则周长=8+8+4=20.
2.C
【解析】
试题分析:等边三角形性质:
1三边相等
2三个角都相等
3三个角都等于60°
4高线、腰、底边中线三线合一.
三角形为等边三角形,等边三角形三边相等,三个角也相等.
解:已知三角形为等边三角形,所以∠A=∠B=∠C==60°.
故选C.
3.D.
【解析】
试题分析:根据等腰三角形的性质与三角形三边关系,可知等腰三角形腰长是2,∴2+2=4∴底边不可能是4.www.21-cn-jy.com
故选:D.
4.C.
【解析】
试题分析:∵AB=AC,∴∠C=∠B=40°,∴∠A=180°﹣∠B﹣∠C=180°﹣40°﹣40°=100°,∵DE∥AC,∴∠BED=∠A=100°.故选C.【来源:21·世纪·教育·网】
5.D
【解析】
试题分析:分两种情况,(1)此等腰三角形为锐角三角形时,顶角为600 ;(2)此等腰三角形为钝角三角形时,顶角为1200 ,故选:D.21·世纪*教育网
6.B.
【解析】
试题分析:由角平分线的性质可得DE=EC,则AE+DE=AC=3cm.
故选:B.
7.D
【解析】
试题分析:A可利用SAS来判定全等,故正确;B可利用AAS来判定全等,故正确;C可利用HL判定全等,故正确;D面积相等不一定退出两直角三角形全等,没有相关的判定方法,故不正确.【来源:21cnj*y.co*m】
故选D
8.A
【解析】
试题分析:根据∠ACB=90°,∠ABC=60°,BD平分∠ABC可得:BD=AD=6,根据直角三角形斜边上的中线等于斜边的一半得出CP=3.【出处:21教育名师】
9.B
【解析】
试题分析:作出图形,根据直角三角形两锐角互余可得∠BAC+∠ABC=90°,再根据角平分线的定义可得∠OAB+∠OBA=45°,然后根据三角形的内角和定理列式计算即可得解.
解:如图,∵∠C=90°,
∴∠BAC+∠ABC=180°﹣90°=90°,
∵AD、BE分别是∠BAC和∠ABC的平分线,
∴∠OAB+∠OBA=×90°=45°,
∴∠AOB=180°﹣(∠OAB+∠OBA)=180°﹣45°=135°.
故选B.
10.A
【解析】
试题分析:结合三角形的内角和为180°逐个分析4个条件,可得出①④中∠C=90°,②③能确定△ABC为锐角三角形,从而得出结论.【版权所有:21教育】
解:①∵∠A+∠B=∠C,且∠A+∠B+∠C=180°,
∴∠C+∠C=180°,即∠C=90°,
此时△ABC为直角三角形,①可以;
②∵∠A=∠B=2∠C,且∠A+∠B+∠C=180°,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,∠A=∠B=2∠C=72°,
△ABC为锐角三角形,②不可以;
③∵∠A=∠B=α∠C,且∠A+∠B+∠C=180°,
∴α∠C+α∠C+∠C=180°,
∴∠C=,∠A=∠B=α∠C=,
△ABC为锐角三角形,③不可以;
④∵∠A﹕∠B﹕∠C=1﹕2﹕3,
∴∠A+∠B=∠C,同①,
此时△ABC为直角三角形,④可以;
综上可知:①④能确定△ABC为直角三角形.
故选A.
11.70°.
【解析】
试题分析:由AB=AC,根据等腰三角形的性质得到∠B=∠C=.
12.75°或30°或120°
【解析】
试题分析:当∠A为顶角等于30°时,可得底角∠B=(180°-30°)=75°,△ABC是等腰三角形,当∠A=∠B=30°时,△ABC是等腰三角形,当∠A=∠C=30°时,则∠B=120°,△ABC是等腰三角形,故答案为:75°或30°或120°.21世纪教育网版权所有
13.72°或°
【解析】
试题分析:根据等腰三角形的性质,分两种情况分别求出原等腰三角形的底角度数.其中一个三角形的三个内角度数为:36°、72°、72°,还有一个三角形的三个内角度数为:°、°、°.www-2-1-cnjy-com
14.(1)3;(2)9.
【解析】
试题分析:(1)先根据线段垂直平分线的性质得出AD=BD,再由△BCD的周长为8可得BC=8﹣5=3;2·1·c·n·j·y
(2)根据(1)中,AD=BD可得BD+CD=AC=5.∵BC=4,∴△BCD的周长=5+4=9.
故答案为:(1)3;(2)9.
15.71°.
【解析】
试题分析:∵在Rt△ABC中,∠ACB=90°,∠A=26°,∴∠B=64°,
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠CED=∠B=64°,
∴∠CDE=180°﹣∠ECD﹣∠CED=71°,
故答案为:71°.
16.57°.
【解析】
试题分析:根据∠1可得三角板中的另一个角为60°-27°=33°,则∠2=90°-33°=57°.
17.1.2
【解析】
试题分析:直角三角形斜边上的中线等于斜边的一半,根据这个定理可得:MC=AM=BM=1.2km.
18.2
【解析】
试题分析:根据等腰三角形的性质可得:AD=BD=8-3=5,根据△BDE≌△ADC可得DE=DC=3,则AE=AD-DE=5-3=2cm.2-1-c-n-j-y
19.3
【解析】
试题分析:过P作PC垂直于MN,由等腰三角形三线合一性质得到MC=CN,求出MC的长,在直角三角形OPC中,利用30度角所对的直角边等于斜边的一半求出OC的长,由OC﹣MC求出OM的长即可.21*cnjy*com
过P作PC⊥MN, ∵PM=PN, ∴C为MN中点,即MC=NC=MN=1,
在Rt△OPC中,∠AOB=60°, ∴∠OPC=30°, ∴OC=OP=4, 则OM=OC﹣MC=4﹣1=3,21*cnjy*com
20.14
【解析】
试题分析:根据等腰三角形三线合一的性质可得BE是△ABC的中线,然后根据直角三角形斜边上的中线等于斜边的一半可得DF=AB,EF=AC,然后判断出DE是△ABC的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半可得DE=BC,然后根据三角形的周长公式列式计算即可得解.
解:∵BE⊥AC,
∴BE是△ABC的中线,
∵AF⊥BC,D是AB的中点,
∴DF=AB=×10=5,EF=AC=×8=4,
∵BE是△ABC的中线,D是AB的中点,
∴DE是△ABC的中位线,
∴DE=BC=×10=5,
∴△DEF的周长=5+4+5=14.
故答案为:14.
21.15°
【解析】
试题分析:先根据△ABC是等边三角形,AD为中线可得出AD⊥BC,∠CAD=30°,再由AD=AE可知∠ADE=∠AED,根据三角形内角和定理即可求出∠ADE的度数,故可得出∠EDC的度数.
试题解析:∵△ABC是等边三角形,AD为中线, ∴AD⊥BC,∠CAD=30°, ∵AD=AE,
∴∠ADE=∠AED===75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
22.证明详见解析.
【解析】
试题分析:根据等边三角形的性质可得AB=AC,∠BAE=∠C=60°,再利用“边角边”证明△ABE和△CAD全等,根据全等三角形对应角相等可得∠1=∠2,然后求出∠BPQ=60°,再根据直角三角形两锐角互余求出∠PBQ=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半证明即可.
试题解析:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
AB=AC,∠BAE=∠C=60°,AE=CD,
∴△ABE≌△CAD(SAS),
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
∵BQ⊥AD,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.
23.详见解析
【解析】(1)∵,
∴,(2分)
∵平分,
∴,(3分)
∴.(5分)
(2)过作于,
∵平分,,
∴,(7分)
∴.(9分)
24.(1)13;(2)30°.
【解析】
试题分析:(1)根据直角三角形斜边中线的性质得出EM=FM=BC=5,进而可求得△EFM的周长;
(2)根据直角三角形斜边中线的性质得出EM=BM,FM=MC,根据等腰三角形的性质和三角形内角和定理得出∠EMC=58°,∠FMC=88°,进而可求得∠FME=88°﹣58°=30°.
试题解析:(1)∵CE⊥BA,M为BC的中点,
∴EM=BC=4,
∵BF⊥CA,M为BC的中点,
∴FM=BC=4,
∴△EFM的周长为:EM+FM+EF=5+5+3=13;
(2)∵EM=BC,M为BC的中点,
∴BM=EM,
∴∠EBM=∠BEM=29°,
∴∠EMC=58°,
∵FM=BC,M为BC的中点,
∴FM=MC,
∴∠MFC=∠ACB=46°,
∴∠FMC=88°,
∴∠FME=88°﹣58°=30°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
