山东省泰安市泰山区2015-2016学年九年级(下)期末数学试卷(五四学制)(解析版)
文档属性
| 名称 | 山东省泰安市泰山区2015-2016学年九年级(下)期末数学试卷(五四学制)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 328.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-20 23:40:18 | ||
图片预览



文档简介
2015-2016学年山东省泰安市泰山区九年级(下)期末数学试卷(五四学制)
一、选择题(本大题共14小题,每小题3分,共42分.每小题给出的四个选项中,只有一项是正确的.)
1.与不是同类二次根式的是( )
A.
B.
C.
D.
2.下列二次根式,是最简二次根式的为( )
A.
B.
C.
D.
3.方程(x﹣1)(x+1)=1﹣x的解是( )
A.x=1
B.x=﹣1
C.x=1或x=﹣2
D.x=﹣1或
x=﹣2
4.下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
A.x2+4=0
B.4x2﹣4x+1=0
C.x2+x+3=0
D.x2+2x﹣1=0
5.如图,在△ABC中,DE∥BC,AD=6,BD=3,AE=4,则AC的长为( )
A.9
B.7
C.6
D.5
6.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
7.下列运算正确的是( )
A.
=﹣5
B.﹣=
C.÷=4
D.×=6
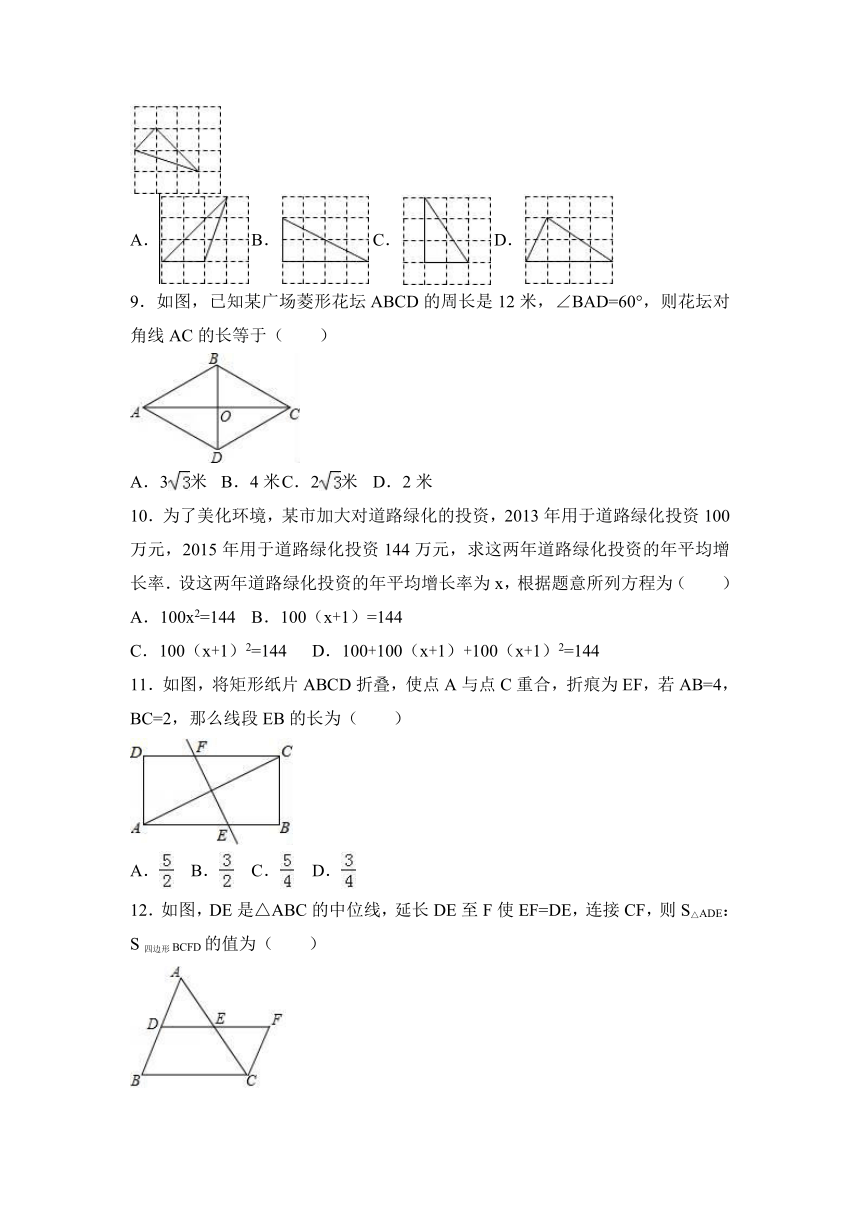
8.下列四个三角形中,与图中的三角形相似的是( )
A.
B.
C.
D.
9.如图,已知某广场菱形花坛ABCD的周长是12米,∠BAD=60°,则花坛对角线AC的长等于( )
A.3米
B.4米
C.2米
D.2米
10.为了美化环境,某市加大对道路绿化的投资,2013年用于道路绿化投资100万元,2015年用于道路绿化投资144万元,求这两年道路绿化投资的年平均增长率.设这两年道路绿化投资的年平均增长率为x,根据题意所列方程为( )
A.100x2=144
B.100(x+1)=144
C.100(x+1)2=144
D.100+100(x+1)+100(x+1)2=144
11.如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EB的长为( )
A.
B.
C.
D.
12.如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
A.1:3
B.2:3
C.2:5
D.1:4
13.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
14.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:
①∠BAE=30°,②△ABE∽△ECF,③AE⊥EF,④AE=2EF,⑤△ABE∽△AEF.
其中正确结论的个数为( )
A.2
B.3
C.4
D.5
二、填空题(本大题共7小题,每小题3分,共21分.只要求填写最后结果)
15.若将方程x2+6x=7化为(x+m)2=16,则m= .
16.一元二次方程x2+2x﹣m﹣1=0总有实数根,则m应满足的条件是 .
17.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为 度.
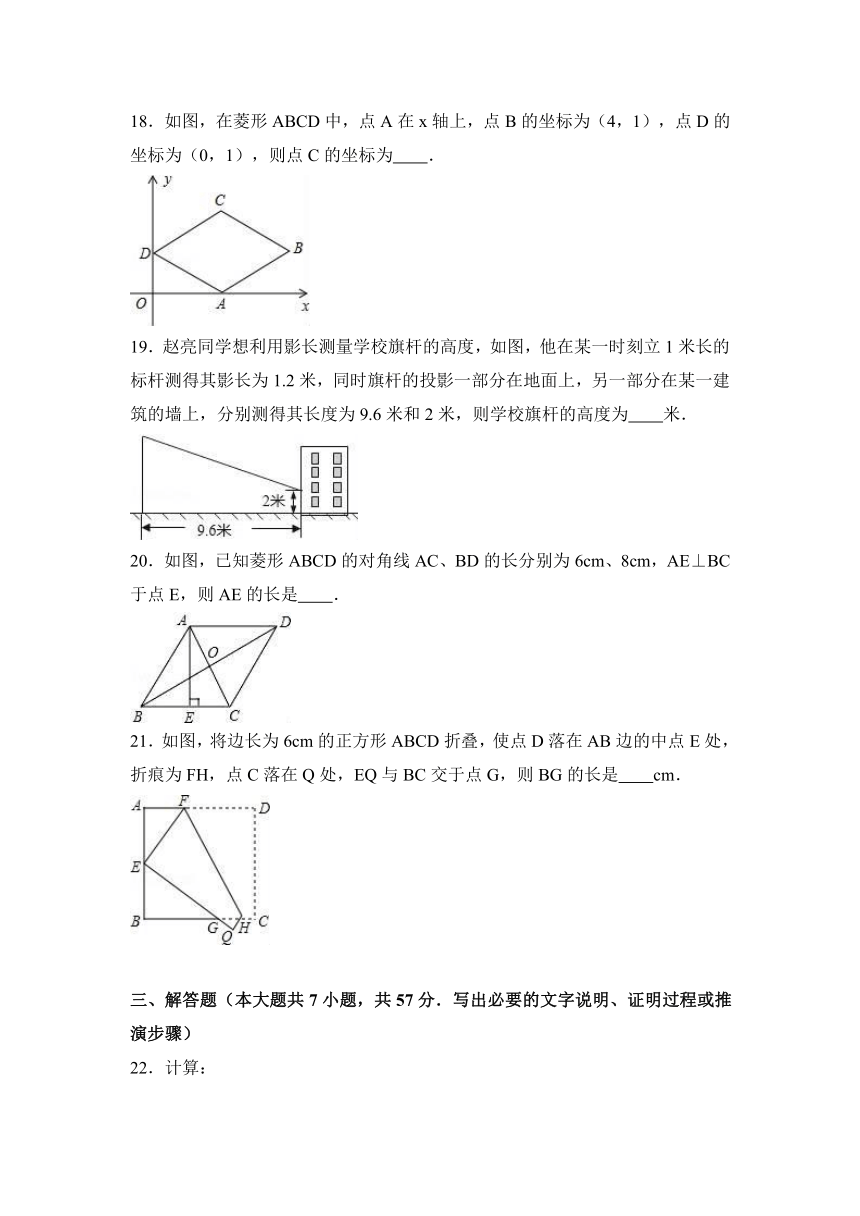
18.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),则点C的坐标为 .
19.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为 米.
20.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是 .
21.如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则BG的长是 cm.
三、解答题(本大题共7小题,共57分.写出必要的文字说明、证明过程或推演步骤)
22.计算:
(1)+﹣(3﹣);
(2)9﹣3÷(﹣).
23.解下列方程
(1)3x2﹣3=2x(用配方法解);
(2)(x﹣2)(x+3)=﹣5.
24.已知:如图,在平行四边形ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:AF=CE;
(2)连接AC,当CA=CB时,判断四边形AECF是否为矩形?并给予证明.
25.已知:如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
(1)求证:∠DAE=∠DCE;
(2)求证:AE2=EF EG.
26.国庆期间,盱眙旅游业非常火爆.某宾馆客房部有60个房间供旅客居住,当每个房间的定价为每天200元,房间可以注满.当每个房间每天的定价每提高10元,就会有一个房间空闲,对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用;设每个房间每天的定价增加x元,则
(1)房间每天的入住间数 间(用x的代数式表示);
(2)该宾馆每天的房间所收费用为 元(用x的代数式表示);
(3)若该宾馆客房部希望每天的利润为14000元,则每个房间的定价应为多少元?(为了吸引游客,每个房间的定价不会高于500元)
27.已知:如图,在边长为8的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
28.已知:如图,在△ABC中,AB=AC=5cm,BC=6cm,点D在BC边上运动,作∠ADE=∠B,DE交AC于E.
(1)求证:△ABD∽△DCE;
(2)当AD=DE时,求BD的长;
(3)当AE=DE时,求BD的长.
2015-2016学年山东省泰安市泰山区九年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(本大题共14小题,每小题3分,共42分.每小题给出的四个选项中,只有一项是正确的.)
1.与不是同类二次根式的是( )
A.
B.
C.
D.
【考点】同类二次根式.
【分析】把各选项化成最简二次根式,然后选择答案即可.
【解答】解:A、=,与是同类二次根式,故本选项错误;
B、=2,与是同类二次根式,故本选项错误;
C、=4,与是同类二次根式,故本选项错误;
D、=2,与不是同类二次根式,故本选项正确.
故选D.
2.下列二次根式,是最简二次根式的为( )
A.
B.
C.
D.
【考点】最简二次根式.
【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
【解答】解:A、=2,不是最简二次根式,故本选项错误;
B、是最简二次根式,故本选项正确;
C、=2,不是最简二次根式,故本选项错误;
D、=不是最简二次根式,故本选项错误;
故选B.
3.方程(x﹣1)(x+1)=1﹣x的解是( )
A.x=1
B.x=﹣1
C.x=1或x=﹣2
D.x=﹣1或
x=﹣2
【考点】解一元二次方程-因式分解法.
【分析】先移项,再提公因式即可.
【解答】解:(x﹣1)(x+1)+(x﹣1)=0,
(x﹣1)(x+1+1)=0,
(x+2)(x﹣1)=0
x+2=0或x﹣1=0,
x=﹣2或1,
故选C.
4.下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
A.x2+4=0
B.4x2﹣4x+1=0
C.x2+x+3=0
D.x2+2x﹣1=0
【考点】根的判别式.
【分析】根据一元二次方程根的判别式,分别计算△的值,根据△>0,方程有两个不相等的实数根;△=0,方程有两个相等的实数根;△<0,方程没有实数根,进行判断.
【解答】解:A、△=﹣16<0,方程没有实数根;
B、△=0,方程有两个相等的实数根;
C、△=1﹣12=﹣11<0,方程没有实数根;
D、△=4+4=8>0,方程有两个不相等的实数根.
故选D.
5.如图,在△ABC中,DE∥BC,AD=6,BD=3,AE=4,则AC的长为( )
A.9
B.7
C.6
D.5
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理,由DE∥BC得,然后利用比例性质求EC和AC的值即可.
【解答】解:∵DE∥BC,AD=6,BD=3,AE=4,
∴,
∴EC=2,
∴AC=2+4=6.
故选C
6.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
【考点】正方形的判定;平行四边形的性质;菱形的判定;矩形的判定.
【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.
【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;
综上所述,符合题意是D选项;
故选:D.
7.下列运算正确的是( )
A.
=﹣5
B.﹣=
C.÷=4
D.×=6
【考点】二次根式的混合运算.
【分析】原式各项计算得到结果,即可作出判断.
【解答】解:A、原式=|﹣5|=5,错误;
B、原式=2﹣=,正确;
C、原式=2÷=2,错误;
D、原式=,错误,
故选B
8.下列四个三角形中,与图中的三角形相似的是( )
A.
B.
C.
D.
【考点】相似三角形的判定.
【分析】本题主要应用两三角形相似的判定定理,三边对应成比例,做题即可.
【解答】解:设单位正方形的边长为1,给出的三角形三边长分别为,2,.
A、三角形三边2,,3,与给出的三角形的各边不成比例,故A选项错误;
B、三角形三边2,4,2,与给出的三角形的各边成正比例,故B选项正确;
C、三角形三边2,3,,与给出的三角形的各边不成比例,故C选项错误;
D、三角形三边,4,,与给出的三角形的各边不成比例,故D选项错误.
故选:B.
9.如图,已知某广场菱形花坛ABCD的周长是12米,∠BAD=60°,则花坛对角线AC的长等于( )
A.3米
B.4米
C.2米
D.2米
【考点】菱形的性质.
【分析】由菱形花坛ABCD的周长是12米,∠BAD=60°,可求得边长AD的长,AC⊥BD,且∠CAD=30°,则可求得OA的长,继而求得答案.
【解答】解:∵菱形花坛ABCD的周长是12米,∠BAD=60°,
∴AC⊥BD,AC=2OA,∠CAD=∠BAD=30°,AD=3米,
∴OA=AD cos30°=3×=(米),
∴AC=2OA=3米.
故选:A.
10.为了美化环境,某市加大对道路绿化的投资,2013年用于道路绿化投资100万元,2015年用于道路绿化投资144万元,求这两年道路绿化投资的年平均增长率.设这两年道路绿化投资的年平均增长率为x,根据题意所列方程为( )
A.100x2=144
B.100(x+1)=144
C.100(x+1)2=144
D.100+100(x+1)+100(x+1)2=144
【考点】由实际问题抽象出一元二次方程.
【分析】一般用增长后的量=增长前的量×(1+增长率),设这两年绿化投资的年平均增长率为x,根据“2013年用于道路绿化投资100万元,2015年用于道路绿化投资144万元”,可得出方程.
【解答】解:设这两年绿化投资的年平均增长率为x,那么依题意得:
100(1+x)2=144.
故选:C.
11.如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EB的长为( )
A.
B.
C.
D.
【考点】翻折变换(折叠问题).
【分析】先由折叠得出CE=AE=4﹣AE,再用勾股定理求解即可.
【解答】解:如图,连接CE,
∵四边形ABCD是矩形,
∴∠B=90°,
由折叠得,CE=AE,
∵AB=AE+BE=4,
∴CE=AE=4﹣BE,
在Rt△BCE中,BC=2,
∴CE2﹣BE2=BC2,
∴(4﹣BE)2﹣BE2=4,
∴BE=,
故选B.
12.如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
A.1:3
B.2:3
C.2:5
D.1:4
【考点】相似三角形的判定与性质;三角形中位线定理.
【分析】先利用SAS证明△ADE≌△CFE得出S△ADE=S△CFE,再由DE为中位线,判断△ADE∽△ABC,且相似比为1:2,利用相似三角形的面积比等于相似比,得到S△ADE:S△ABC=1:4,则即===.
【解答】解:∵DE为△ABC的中位线,
∴AE=CE.
在△ADE与△CFE中,
∵,
∴△ADE≌△CFE(SAS),
∴S△ADE=S△CFE.
∵DE为△ABC的中位线,
∴△ADE∽△ABC,且相似比为1:2,
∴=,即===,
故选:D.
13.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
【考点】位似变换;坐标与图形性质.
【分析】利用位似图形的性质结合两图形的位似比进而得出C点坐标.
【解答】解:∵线段AB的两个端点坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,
∴端点C的横坐标和纵坐标都变为A点的一半,
∴端点C的坐标为:(3,3).
故选:A.
14.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:
①∠BAE=30°,②△ABE∽△ECF,③AE⊥EF,④AE=2EF,⑤△ABE∽△AEF.
其中正确结论的个数为( )
A.2
B.3
C.4
D.5
【考点】四边形综合题.
【分析】先由线段的关系得出==2,即可判断出①错误,再利用两边对应成比例,夹角相等得出△ABE∽△ECF,△ABE∽△AEF,最后用同角的余角相等,即可得出②③④⑤正确.
【解答】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠D=90°
∵E是BC的中点,
∴AE=CE=BC=AB,
在Rt△ABE中,tan∠BAE==<,
∵tan30°=,
∴∠BAE<30°,
所以①错误;
∴=2
∵CD=4CF,
∴=2,
∴=,
∵∠B=∠C,
∴△ABE∽△ECF,
∴=2,
∴AE=2EF,
所以②④正确;
∵△ABE∽△ECF,
∴∠BAE=∠CEF,
∵∠BAE+∠AEB=90°,
∴∠AEB+∠CEF=90°,
∴∠AEF=90°,
∴AE⊥EF,
所以③正确;
∵=2,
=2,
∴,
∵∠B=∠AEF=90°,
∴△ABE∽△AEF,
所以⑤正确,
即:正确的有②③④⑤四个;
故选C.
二、填空题(本大题共7小题,每小题3分,共21分.只要求填写最后结果)
15.若将方程x2+6x=7化为(x+m)2=16,则m= 3 .
【考点】解一元二次方程-配方法.
【分析】此题实际上是利用配方法解方程.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
【解答】解:在方程x2+6x=7的两边同时加上一次项系数的一半的平方,得
x2+6x+32=7+32,
配方,得
(x+3)2=16.
所以,m=3.
故答案为:3.
16.一元二次方程x2+2x﹣m﹣1=0总有实数根,则m应满足的条件是 m≥﹣2 .
【考点】根的判别式.
【分析】根据根的判别式,令△≥0,建立关于m的不等式,解答即可.
【解答】解:∵方程x2+2x﹣m﹣1=0总有实数根,
∴△≥0,
即4﹣4(﹣m﹣1)≥0,
∴4m≥﹣8,
∴m≥﹣2.
故答案为:m≥﹣2.
17.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为 60 度.
【考点】正方形的性质;等边三角形的性质.
【分析】根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC.
【解答】解:∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
故答案为:60.
18.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),则点C的坐标为 (2,2) .
【考点】菱形的性质;坐标与图形性质.
【分析】首先连接AC,BD相较于点E,由在菱形ABCD中,点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),可求得点E的坐标,继而求得答案.
【解答】解:连接AC,BD相较于点E,
∵四边形ABCD是菱形,
∴AE=CE,BE=DE,AC⊥BD,
∵点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),
∴BD=4,AE=1,
∴DE=BD=2,AC=2AE=2,
∴点C的坐标为:(2,2).
故答案为:(2,2).
19.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为 10 米.
【考点】相似三角形的应用.
【分析】利用相似三角形对应线段成比例,求解即可.
【解答】解:1米长的标杆测得其影长为1.2米,即某一时刻实际高度和影长之比为定值,所以墙上的2米投射到地面上实际为2.4米,即旗杆影长为12米,因此旗杆总高度为10米.
20.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是 cm .
【考点】菱形的性质.
【分析】根据菱形的性质得出BO、CO的长,在RT△BOC中求出BC,利用菱形面积等于对角线乘积的一半,也等于BC×AE,可得出AE的长度.
【解答】解:∵四边形ABCD是菱形,
∴CO=AC=3cm,BO=BD=4cm,AO⊥BO,
∴BC==5cm,
∴S菱形ABCD==×6×8=24cm2,
∵S菱形ABCD=BC×AE,
∴BC×AE=24,
∴AE==cm.
故答案为:
cm.
21.如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则BG的长是 4 cm.
【考点】翻折变换(折叠问题);正方形的性质.
【分析】根据翻折变换的性质可得EF=FD,设AF=x,表示出EF,根据线段中点的定义求出AE=BE=3,再利用勾股定理列方程求出AF,然后求出△AEF和△BGE相似,根据相似三角形对应边成比例列式计算即可得解.
【解答】解:∵正方形ABCD折叠点D落在AB边的中点E处,
∴EF=FD,
设AF=x,则EF=6﹣x,
∵点E是AB的中点,
∴AE=BE=×6=3,
在Rt△AEF中,由勾股定理得,AE2+AF2=EF2,
即32+x2=(6﹣x)2,
解得x=,
∵∠FEG=90°,
∴∠AEF+∠BEG=90°,
∵∠BEG+∠BGE=90°,
∴∠AEF=∠BGE,
又∵∠A=∠B=90°,
∴△AEF∽△BGE,
∴=,
∴BG===4cm.
故答案为:4.
三、解答题(本大题共7小题,共57分.写出必要的文字说明、证明过程或推演步骤)
22.计算:
(1)+﹣(3﹣);
(2)9﹣3÷(﹣).
【考点】二次根式的混合运算.
【分析】(1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先进行二次根式的除法运算,然后化简即可.
【解答】解:(1)原式=+2﹣+
=2+;
(2)原式=27+3××
=27+.
23.解下列方程
(1)3x2﹣3=2x(用配方法解);
(2)(x﹣2)(x+3)=﹣5.
【考点】解一元二次方程-公式法;解一元二次方程-配方法.
【分析】(1)用配方法解,首先把系数化为1,移项,把常数项移到等号的右边,然后在方程的左右两边同时加上一次项系数的一半,即可使左边是完全平方式,右边是常数,即可求解.
(2)确定a,b,c的值,然后检验方程是否有解,若有解,代入公式即可求解.
【解答】(1)解:方程变形得:3x2﹣2x=3,
方程两边同除以3,得:x2﹣x=1,
配方,得x2﹣x+=1+,
所以(x﹣)2=,
所以,x﹣=±
所以x1=,x2=;
(2)解:整理得:x2+x﹣1=0,
这里a=1,b=1,c=﹣1,b2﹣4ac=1+4=5,
∴x==
∴x1=,x2=.
24.已知:如图,在平行四边形ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:AF=CE;
(2)连接AC,当CA=CB时,判断四边形AECF是否为矩形?并给予证明.
【考点】矩形的判定;全等三角形的判定与性质;平行四边形的性质.
【分析】(1)利用平行四边形的性质,结合全等三角形的判定与性质,进而得出答案;
(2)首先利用平行四边形的性质证明AE∥CF,AE=CF,可证明四边形AECF是平行四边形,再根据AC=BC,E是AB的中点,可根据等腰三角形底边上的中线与底边上的高线重合证明∠AEC=90°,即可证明平行四边形AECF是矩形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴BC=AD,∠B=∠D,AB=CD,
∵E、F分别是AB、CD的中点,
∴BE=DF=AE=CF,
在△BEC和△DFA中,
,
∴△BEC≌△DFA(SAS),
∴AF=CE;
(2)四边形AECF是矩形,
证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∵AE=CF,∴四边形AECF是平行四边形,
∵AC=BC,E是AB的中点,∴CE⊥AB,
∴∠AEC=90°,∴平行四边形AECF是矩形.
25.已知:如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
(1)求证:∠DAE=∠DCE;
(2)求证:AE2=EF EG.
【考点】相似三角形的判定与性质;菱形的性质.
【分析】(1)根据四边形ABCD是菱形可得出△ADE≌△CDE,利用全等三角形的性质即可证明∠DAE=∠DCE;
(2)首先利用平行线的性质得出∠DAE=∠G,进而得出∠G=∠DCE,进而可证明△ECF∽△EGC,由相似三角形的性质即可证明AE2=EF EG.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDB;
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE;
(2)证明:∵四边形ABCD是菱形,
∴AD∥BC,∠DAG=∠G,
∵∠DAE=∠DCE,
∴∠DCE=∠G,
∵∠CEF=∠GEC
∴△ECF∽△EGC,
∴,
∴CE2=EF EG,
∵△ADE≌△CDE,
∴EA=EC,
∴AE2=EF EG.
26.国庆期间,盱眙旅游业非常火爆.某宾馆客房部有60个房间供旅客居住,当每个房间的定价为每天200元,房间可以注满.当每个房间每天的定价每提高10元,就会有一个房间空闲,对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用;设每个房间每天的定价增加x元,则
(1)房间每天的入住间数 60﹣ 间(用x的代数式表示);
(2)该宾馆每天的房间所收费用为 ﹣x2+40x+12000 元(用x的代数式表示);
(3)若该宾馆客房部希望每天的利润为14000元,则每个房间的定价应为多少元?(为了吸引游客,每个房间的定价不会高于500元)
【考点】一元二次方程的应用.
【分析】(1)根据题意可得房间每天的入住量=60个房间﹣每个房间每天的定价增加的钱数÷10;
(2)已知每天定价增加为x元,则每天要元.则宾馆每天的房间收费=每天的实际定价×房间每天的入住量;
(3)支出费用为20×(60﹣),则利润w=(60﹣)﹣20×(60﹣),把w=14000代入求得相应的x的值.
【解答】解:(1)由题意得:60﹣.
故答案是:60﹣.
(2)(60﹣)=﹣x2+40x+12000.
故答案是:﹣x2+40x+12000.
(3)依题意得:(60﹣)﹣20×(60﹣)=14000,
整理,得
x2﹣420x+32000=0,
解得x=320或x=100,
为了吸引游客,每个房间的定价应为300元.
答:为了吸引游客,每个房间的定价应为300元.
27.已知:如图,在边长为8的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
【考点】翻折变换(折叠问题);全等三角形的判定与性质;正方形的性质.
【分析】(1)先根据正方形性质得:AD=AB,∠B=∠D=90°,由对折得:AD=AF,∠D=∠AFE=90°,则AF=AB,根据HL证明△ABG≌△AFG;
(2)根据全等得:BG=FG,设BG=GF=x,在Rt△CEG中,根据勾股定理列方程解出即可.
【解答】证明:(1)在正方形ABCD中,
∴AD=AB,∠D=∠B=90°
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
∴△ABG≌△AFG(HL)
(2)∵△ABG≌△AFG,
∴BG=FG,
设BG=GF=x,则GC=8﹣x,
∵E为CD的中点,
∴CE=EF=ED=4
∴EG=4+x,
∴在Rt△CEG中,
42+(8﹣x)2=(4+x)2,
解得x=,
∴BG=.
28.已知:如图,在△ABC中,AB=AC=5cm,BC=6cm,点D在BC边上运动,作∠ADE=∠B,DE交AC于E.
(1)求证:△ABD∽△DCE;
(2)当AD=DE时,求BD的长;
(3)当AE=DE时,求BD的长.
【考点】相似形综合题.
【分析】(1)欲证明△ABD∽△DCE,只要证明∠BAD=∠CDE,∠B=∠C即可.
(2)当AD=DE时,△ABD≌△DCE,AB=DC=5,由此即可解决问题.
(3)只要证明△CAB∽△CDA,得=,求出CD即可解决问题.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠BAD+∠B,∠ADC=∠ADE+∠EDC
∵∠ADE=∠B
∴∠BAD=∠EDC,
又∵∠B=∠C
∴△ABD∽△DCE.
(2)解:当AD=DE时,
由(1)知△ABD∽△DCE,
∴△ABD≌△DCE,
∴AB=CD=5,
∴BD=BC﹣DC=6﹣5=1.
(3)解:当AE=DE时,可知∠EAD=∠EDA,
∵∠BAD=∠EDC,
∴∠CAB=∠CDA,
又∵∠C=∠C,
∴△CAB∽△CDA,
∴=,
∴=,
∴CD=
∴BD=BC﹣CD=6﹣=.
2017年2月19日
一、选择题(本大题共14小题,每小题3分,共42分.每小题给出的四个选项中,只有一项是正确的.)
1.与不是同类二次根式的是( )
A.
B.
C.
D.
2.下列二次根式,是最简二次根式的为( )
A.
B.
C.
D.
3.方程(x﹣1)(x+1)=1﹣x的解是( )
A.x=1
B.x=﹣1
C.x=1或x=﹣2
D.x=﹣1或
x=﹣2
4.下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
A.x2+4=0
B.4x2﹣4x+1=0
C.x2+x+3=0
D.x2+2x﹣1=0
5.如图,在△ABC中,DE∥BC,AD=6,BD=3,AE=4,则AC的长为( )
A.9
B.7
C.6
D.5
6.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
7.下列运算正确的是( )
A.
=﹣5
B.﹣=
C.÷=4
D.×=6
8.下列四个三角形中,与图中的三角形相似的是( )
A.
B.
C.
D.
9.如图,已知某广场菱形花坛ABCD的周长是12米,∠BAD=60°,则花坛对角线AC的长等于( )
A.3米
B.4米
C.2米
D.2米
10.为了美化环境,某市加大对道路绿化的投资,2013年用于道路绿化投资100万元,2015年用于道路绿化投资144万元,求这两年道路绿化投资的年平均增长率.设这两年道路绿化投资的年平均增长率为x,根据题意所列方程为( )
A.100x2=144
B.100(x+1)=144
C.100(x+1)2=144
D.100+100(x+1)+100(x+1)2=144
11.如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EB的长为( )
A.
B.
C.
D.
12.如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
A.1:3
B.2:3
C.2:5
D.1:4
13.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
14.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:
①∠BAE=30°,②△ABE∽△ECF,③AE⊥EF,④AE=2EF,⑤△ABE∽△AEF.
其中正确结论的个数为( )
A.2
B.3
C.4
D.5
二、填空题(本大题共7小题,每小题3分,共21分.只要求填写最后结果)
15.若将方程x2+6x=7化为(x+m)2=16,则m= .
16.一元二次方程x2+2x﹣m﹣1=0总有实数根,则m应满足的条件是 .
17.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为 度.
18.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),则点C的坐标为 .
19.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为 米.
20.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是 .
21.如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则BG的长是 cm.
三、解答题(本大题共7小题,共57分.写出必要的文字说明、证明过程或推演步骤)
22.计算:
(1)+﹣(3﹣);
(2)9﹣3÷(﹣).
23.解下列方程
(1)3x2﹣3=2x(用配方法解);
(2)(x﹣2)(x+3)=﹣5.
24.已知:如图,在平行四边形ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:AF=CE;
(2)连接AC,当CA=CB时,判断四边形AECF是否为矩形?并给予证明.
25.已知:如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
(1)求证:∠DAE=∠DCE;
(2)求证:AE2=EF EG.
26.国庆期间,盱眙旅游业非常火爆.某宾馆客房部有60个房间供旅客居住,当每个房间的定价为每天200元,房间可以注满.当每个房间每天的定价每提高10元,就会有一个房间空闲,对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用;设每个房间每天的定价增加x元,则
(1)房间每天的入住间数 间(用x的代数式表示);
(2)该宾馆每天的房间所收费用为 元(用x的代数式表示);
(3)若该宾馆客房部希望每天的利润为14000元,则每个房间的定价应为多少元?(为了吸引游客,每个房间的定价不会高于500元)
27.已知:如图,在边长为8的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
28.已知:如图,在△ABC中,AB=AC=5cm,BC=6cm,点D在BC边上运动,作∠ADE=∠B,DE交AC于E.
(1)求证:△ABD∽△DCE;
(2)当AD=DE时,求BD的长;
(3)当AE=DE时,求BD的长.
2015-2016学年山东省泰安市泰山区九年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(本大题共14小题,每小题3分,共42分.每小题给出的四个选项中,只有一项是正确的.)
1.与不是同类二次根式的是( )
A.
B.
C.
D.
【考点】同类二次根式.
【分析】把各选项化成最简二次根式,然后选择答案即可.
【解答】解:A、=,与是同类二次根式,故本选项错误;
B、=2,与是同类二次根式,故本选项错误;
C、=4,与是同类二次根式,故本选项错误;
D、=2,与不是同类二次根式,故本选项正确.
故选D.
2.下列二次根式,是最简二次根式的为( )
A.
B.
C.
D.
【考点】最简二次根式.
【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
【解答】解:A、=2,不是最简二次根式,故本选项错误;
B、是最简二次根式,故本选项正确;
C、=2,不是最简二次根式,故本选项错误;
D、=不是最简二次根式,故本选项错误;
故选B.
3.方程(x﹣1)(x+1)=1﹣x的解是( )
A.x=1
B.x=﹣1
C.x=1或x=﹣2
D.x=﹣1或
x=﹣2
【考点】解一元二次方程-因式分解法.
【分析】先移项,再提公因式即可.
【解答】解:(x﹣1)(x+1)+(x﹣1)=0,
(x﹣1)(x+1+1)=0,
(x+2)(x﹣1)=0
x+2=0或x﹣1=0,
x=﹣2或1,
故选C.
4.下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
A.x2+4=0
B.4x2﹣4x+1=0
C.x2+x+3=0
D.x2+2x﹣1=0
【考点】根的判别式.
【分析】根据一元二次方程根的判别式,分别计算△的值,根据△>0,方程有两个不相等的实数根;△=0,方程有两个相等的实数根;△<0,方程没有实数根,进行判断.
【解答】解:A、△=﹣16<0,方程没有实数根;
B、△=0,方程有两个相等的实数根;
C、△=1﹣12=﹣11<0,方程没有实数根;
D、△=4+4=8>0,方程有两个不相等的实数根.
故选D.
5.如图,在△ABC中,DE∥BC,AD=6,BD=3,AE=4,则AC的长为( )
A.9
B.7
C.6
D.5
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理,由DE∥BC得,然后利用比例性质求EC和AC的值即可.
【解答】解:∵DE∥BC,AD=6,BD=3,AE=4,
∴,
∴EC=2,
∴AC=2+4=6.
故选C
6.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
【考点】正方形的判定;平行四边形的性质;菱形的判定;矩形的判定.
【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.
【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;
综上所述,符合题意是D选项;
故选:D.
7.下列运算正确的是( )
A.
=﹣5
B.﹣=
C.÷=4
D.×=6
【考点】二次根式的混合运算.
【分析】原式各项计算得到结果,即可作出判断.
【解答】解:A、原式=|﹣5|=5,错误;
B、原式=2﹣=,正确;
C、原式=2÷=2,错误;
D、原式=,错误,
故选B
8.下列四个三角形中,与图中的三角形相似的是( )
A.
B.
C.
D.
【考点】相似三角形的判定.
【分析】本题主要应用两三角形相似的判定定理,三边对应成比例,做题即可.
【解答】解:设单位正方形的边长为1,给出的三角形三边长分别为,2,.
A、三角形三边2,,3,与给出的三角形的各边不成比例,故A选项错误;
B、三角形三边2,4,2,与给出的三角形的各边成正比例,故B选项正确;
C、三角形三边2,3,,与给出的三角形的各边不成比例,故C选项错误;
D、三角形三边,4,,与给出的三角形的各边不成比例,故D选项错误.
故选:B.
9.如图,已知某广场菱形花坛ABCD的周长是12米,∠BAD=60°,则花坛对角线AC的长等于( )
A.3米
B.4米
C.2米
D.2米
【考点】菱形的性质.
【分析】由菱形花坛ABCD的周长是12米,∠BAD=60°,可求得边长AD的长,AC⊥BD,且∠CAD=30°,则可求得OA的长,继而求得答案.
【解答】解:∵菱形花坛ABCD的周长是12米,∠BAD=60°,
∴AC⊥BD,AC=2OA,∠CAD=∠BAD=30°,AD=3米,
∴OA=AD cos30°=3×=(米),
∴AC=2OA=3米.
故选:A.
10.为了美化环境,某市加大对道路绿化的投资,2013年用于道路绿化投资100万元,2015年用于道路绿化投资144万元,求这两年道路绿化投资的年平均增长率.设这两年道路绿化投资的年平均增长率为x,根据题意所列方程为( )
A.100x2=144
B.100(x+1)=144
C.100(x+1)2=144
D.100+100(x+1)+100(x+1)2=144
【考点】由实际问题抽象出一元二次方程.
【分析】一般用增长后的量=增长前的量×(1+增长率),设这两年绿化投资的年平均增长率为x,根据“2013年用于道路绿化投资100万元,2015年用于道路绿化投资144万元”,可得出方程.
【解答】解:设这两年绿化投资的年平均增长率为x,那么依题意得:
100(1+x)2=144.
故选:C.
11.如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EB的长为( )
A.
B.
C.
D.
【考点】翻折变换(折叠问题).
【分析】先由折叠得出CE=AE=4﹣AE,再用勾股定理求解即可.
【解答】解:如图,连接CE,
∵四边形ABCD是矩形,
∴∠B=90°,
由折叠得,CE=AE,
∵AB=AE+BE=4,
∴CE=AE=4﹣BE,
在Rt△BCE中,BC=2,
∴CE2﹣BE2=BC2,
∴(4﹣BE)2﹣BE2=4,
∴BE=,
故选B.
12.如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
A.1:3
B.2:3
C.2:5
D.1:4
【考点】相似三角形的判定与性质;三角形中位线定理.
【分析】先利用SAS证明△ADE≌△CFE得出S△ADE=S△CFE,再由DE为中位线,判断△ADE∽△ABC,且相似比为1:2,利用相似三角形的面积比等于相似比,得到S△ADE:S△ABC=1:4,则即===.
【解答】解:∵DE为△ABC的中位线,
∴AE=CE.
在△ADE与△CFE中,
∵,
∴△ADE≌△CFE(SAS),
∴S△ADE=S△CFE.
∵DE为△ABC的中位线,
∴△ADE∽△ABC,且相似比为1:2,
∴=,即===,
故选:D.
13.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
【考点】位似变换;坐标与图形性质.
【分析】利用位似图形的性质结合两图形的位似比进而得出C点坐标.
【解答】解:∵线段AB的两个端点坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,
∴端点C的横坐标和纵坐标都变为A点的一半,
∴端点C的坐标为:(3,3).
故选:A.
14.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:
①∠BAE=30°,②△ABE∽△ECF,③AE⊥EF,④AE=2EF,⑤△ABE∽△AEF.
其中正确结论的个数为( )
A.2
B.3
C.4
D.5
【考点】四边形综合题.
【分析】先由线段的关系得出==2,即可判断出①错误,再利用两边对应成比例,夹角相等得出△ABE∽△ECF,△ABE∽△AEF,最后用同角的余角相等,即可得出②③④⑤正确.
【解答】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠D=90°
∵E是BC的中点,
∴AE=CE=BC=AB,
在Rt△ABE中,tan∠BAE==<,
∵tan30°=,
∴∠BAE<30°,
所以①错误;
∴=2
∵CD=4CF,
∴=2,
∴=,
∵∠B=∠C,
∴△ABE∽△ECF,
∴=2,
∴AE=2EF,
所以②④正确;
∵△ABE∽△ECF,
∴∠BAE=∠CEF,
∵∠BAE+∠AEB=90°,
∴∠AEB+∠CEF=90°,
∴∠AEF=90°,
∴AE⊥EF,
所以③正确;
∵=2,
=2,
∴,
∵∠B=∠AEF=90°,
∴△ABE∽△AEF,
所以⑤正确,
即:正确的有②③④⑤四个;
故选C.
二、填空题(本大题共7小题,每小题3分,共21分.只要求填写最后结果)
15.若将方程x2+6x=7化为(x+m)2=16,则m= 3 .
【考点】解一元二次方程-配方法.
【分析】此题实际上是利用配方法解方程.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
【解答】解:在方程x2+6x=7的两边同时加上一次项系数的一半的平方,得
x2+6x+32=7+32,
配方,得
(x+3)2=16.
所以,m=3.
故答案为:3.
16.一元二次方程x2+2x﹣m﹣1=0总有实数根,则m应满足的条件是 m≥﹣2 .
【考点】根的判别式.
【分析】根据根的判别式,令△≥0,建立关于m的不等式,解答即可.
【解答】解:∵方程x2+2x﹣m﹣1=0总有实数根,
∴△≥0,
即4﹣4(﹣m﹣1)≥0,
∴4m≥﹣8,
∴m≥﹣2.
故答案为:m≥﹣2.
17.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为 60 度.
【考点】正方形的性质;等边三角形的性质.
【分析】根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC.
【解答】解:∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
故答案为:60.
18.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),则点C的坐标为 (2,2) .
【考点】菱形的性质;坐标与图形性质.
【分析】首先连接AC,BD相较于点E,由在菱形ABCD中,点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),可求得点E的坐标,继而求得答案.
【解答】解:连接AC,BD相较于点E,
∵四边形ABCD是菱形,
∴AE=CE,BE=DE,AC⊥BD,
∵点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),
∴BD=4,AE=1,
∴DE=BD=2,AC=2AE=2,
∴点C的坐标为:(2,2).
故答案为:(2,2).
19.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为 10 米.
【考点】相似三角形的应用.
【分析】利用相似三角形对应线段成比例,求解即可.
【解答】解:1米长的标杆测得其影长为1.2米,即某一时刻实际高度和影长之比为定值,所以墙上的2米投射到地面上实际为2.4米,即旗杆影长为12米,因此旗杆总高度为10米.
20.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是 cm .
【考点】菱形的性质.
【分析】根据菱形的性质得出BO、CO的长,在RT△BOC中求出BC,利用菱形面积等于对角线乘积的一半,也等于BC×AE,可得出AE的长度.
【解答】解:∵四边形ABCD是菱形,
∴CO=AC=3cm,BO=BD=4cm,AO⊥BO,
∴BC==5cm,
∴S菱形ABCD==×6×8=24cm2,
∵S菱形ABCD=BC×AE,
∴BC×AE=24,
∴AE==cm.
故答案为:
cm.
21.如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则BG的长是 4 cm.
【考点】翻折变换(折叠问题);正方形的性质.
【分析】根据翻折变换的性质可得EF=FD,设AF=x,表示出EF,根据线段中点的定义求出AE=BE=3,再利用勾股定理列方程求出AF,然后求出△AEF和△BGE相似,根据相似三角形对应边成比例列式计算即可得解.
【解答】解:∵正方形ABCD折叠点D落在AB边的中点E处,
∴EF=FD,
设AF=x,则EF=6﹣x,
∵点E是AB的中点,
∴AE=BE=×6=3,
在Rt△AEF中,由勾股定理得,AE2+AF2=EF2,
即32+x2=(6﹣x)2,
解得x=,
∵∠FEG=90°,
∴∠AEF+∠BEG=90°,
∵∠BEG+∠BGE=90°,
∴∠AEF=∠BGE,
又∵∠A=∠B=90°,
∴△AEF∽△BGE,
∴=,
∴BG===4cm.
故答案为:4.
三、解答题(本大题共7小题,共57分.写出必要的文字说明、证明过程或推演步骤)
22.计算:
(1)+﹣(3﹣);
(2)9﹣3÷(﹣).
【考点】二次根式的混合运算.
【分析】(1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先进行二次根式的除法运算,然后化简即可.
【解答】解:(1)原式=+2﹣+
=2+;
(2)原式=27+3××
=27+.
23.解下列方程
(1)3x2﹣3=2x(用配方法解);
(2)(x﹣2)(x+3)=﹣5.
【考点】解一元二次方程-公式法;解一元二次方程-配方法.
【分析】(1)用配方法解,首先把系数化为1,移项,把常数项移到等号的右边,然后在方程的左右两边同时加上一次项系数的一半,即可使左边是完全平方式,右边是常数,即可求解.
(2)确定a,b,c的值,然后检验方程是否有解,若有解,代入公式即可求解.
【解答】(1)解:方程变形得:3x2﹣2x=3,
方程两边同除以3,得:x2﹣x=1,
配方,得x2﹣x+=1+,
所以(x﹣)2=,
所以,x﹣=±
所以x1=,x2=;
(2)解:整理得:x2+x﹣1=0,
这里a=1,b=1,c=﹣1,b2﹣4ac=1+4=5,
∴x==
∴x1=,x2=.
24.已知:如图,在平行四边形ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:AF=CE;
(2)连接AC,当CA=CB时,判断四边形AECF是否为矩形?并给予证明.
【考点】矩形的判定;全等三角形的判定与性质;平行四边形的性质.
【分析】(1)利用平行四边形的性质,结合全等三角形的判定与性质,进而得出答案;
(2)首先利用平行四边形的性质证明AE∥CF,AE=CF,可证明四边形AECF是平行四边形,再根据AC=BC,E是AB的中点,可根据等腰三角形底边上的中线与底边上的高线重合证明∠AEC=90°,即可证明平行四边形AECF是矩形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴BC=AD,∠B=∠D,AB=CD,
∵E、F分别是AB、CD的中点,
∴BE=DF=AE=CF,
在△BEC和△DFA中,
,
∴△BEC≌△DFA(SAS),
∴AF=CE;
(2)四边形AECF是矩形,
证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∵AE=CF,∴四边形AECF是平行四边形,
∵AC=BC,E是AB的中点,∴CE⊥AB,
∴∠AEC=90°,∴平行四边形AECF是矩形.
25.已知:如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
(1)求证:∠DAE=∠DCE;
(2)求证:AE2=EF EG.
【考点】相似三角形的判定与性质;菱形的性质.
【分析】(1)根据四边形ABCD是菱形可得出△ADE≌△CDE,利用全等三角形的性质即可证明∠DAE=∠DCE;
(2)首先利用平行线的性质得出∠DAE=∠G,进而得出∠G=∠DCE,进而可证明△ECF∽△EGC,由相似三角形的性质即可证明AE2=EF EG.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDB;
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE;
(2)证明:∵四边形ABCD是菱形,
∴AD∥BC,∠DAG=∠G,
∵∠DAE=∠DCE,
∴∠DCE=∠G,
∵∠CEF=∠GEC
∴△ECF∽△EGC,
∴,
∴CE2=EF EG,
∵△ADE≌△CDE,
∴EA=EC,
∴AE2=EF EG.
26.国庆期间,盱眙旅游业非常火爆.某宾馆客房部有60个房间供旅客居住,当每个房间的定价为每天200元,房间可以注满.当每个房间每天的定价每提高10元,就会有一个房间空闲,对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用;设每个房间每天的定价增加x元,则
(1)房间每天的入住间数 60﹣ 间(用x的代数式表示);
(2)该宾馆每天的房间所收费用为 ﹣x2+40x+12000 元(用x的代数式表示);
(3)若该宾馆客房部希望每天的利润为14000元,则每个房间的定价应为多少元?(为了吸引游客,每个房间的定价不会高于500元)
【考点】一元二次方程的应用.
【分析】(1)根据题意可得房间每天的入住量=60个房间﹣每个房间每天的定价增加的钱数÷10;
(2)已知每天定价增加为x元,则每天要元.则宾馆每天的房间收费=每天的实际定价×房间每天的入住量;
(3)支出费用为20×(60﹣),则利润w=(60﹣)﹣20×(60﹣),把w=14000代入求得相应的x的值.
【解答】解:(1)由题意得:60﹣.
故答案是:60﹣.
(2)(60﹣)=﹣x2+40x+12000.
故答案是:﹣x2+40x+12000.
(3)依题意得:(60﹣)﹣20×(60﹣)=14000,
整理,得
x2﹣420x+32000=0,
解得x=320或x=100,
为了吸引游客,每个房间的定价应为300元.
答:为了吸引游客,每个房间的定价应为300元.
27.已知:如图,在边长为8的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
【考点】翻折变换(折叠问题);全等三角形的判定与性质;正方形的性质.
【分析】(1)先根据正方形性质得:AD=AB,∠B=∠D=90°,由对折得:AD=AF,∠D=∠AFE=90°,则AF=AB,根据HL证明△ABG≌△AFG;
(2)根据全等得:BG=FG,设BG=GF=x,在Rt△CEG中,根据勾股定理列方程解出即可.
【解答】证明:(1)在正方形ABCD中,
∴AD=AB,∠D=∠B=90°
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
∴△ABG≌△AFG(HL)
(2)∵△ABG≌△AFG,
∴BG=FG,
设BG=GF=x,则GC=8﹣x,
∵E为CD的中点,
∴CE=EF=ED=4
∴EG=4+x,
∴在Rt△CEG中,
42+(8﹣x)2=(4+x)2,
解得x=,
∴BG=.
28.已知:如图,在△ABC中,AB=AC=5cm,BC=6cm,点D在BC边上运动,作∠ADE=∠B,DE交AC于E.
(1)求证:△ABD∽△DCE;
(2)当AD=DE时,求BD的长;
(3)当AE=DE时,求BD的长.
【考点】相似形综合题.
【分析】(1)欲证明△ABD∽△DCE,只要证明∠BAD=∠CDE,∠B=∠C即可.
(2)当AD=DE时,△ABD≌△DCE,AB=DC=5,由此即可解决问题.
(3)只要证明△CAB∽△CDA,得=,求出CD即可解决问题.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠BAD+∠B,∠ADC=∠ADE+∠EDC
∵∠ADE=∠B
∴∠BAD=∠EDC,
又∵∠B=∠C
∴△ABD∽△DCE.
(2)解:当AD=DE时,
由(1)知△ABD∽△DCE,
∴△ABD≌△DCE,
∴AB=CD=5,
∴BD=BC﹣DC=6﹣5=1.
(3)解:当AE=DE时,可知∠EAD=∠EDA,
∵∠BAD=∠EDC,
∴∠CAB=∠CDA,
又∵∠C=∠C,
∴△CAB∽△CDA,
∴=,
∴=,
∴CD=
∴BD=BC﹣CD=6﹣=.
2017年2月19日
同课章节目录
