26.1.3 反比例函数的几何性质 教案
文档属性
| 名称 | 26.1.3 反比例函数的几何性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 318.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 00:00:00 | ||
图片预览

文档简介
26.1.3
反比例函数K的几何意义
教案
一、授课目的:让学生理解反比例函数的概念及几种等价形式;能够快速绘出给定反比例函数的图像;掌握反比例函数的性质(对称性,变化趋势等),并应用解决数学问题(如比较函数值大小,求对称点坐标等)。
重点掌握反比例函数中的比例系数k的几何意义。
二、考点分析:反比例函数是历年中考数学的一个重要考点章节,且多以大题的形式出现,常常结合三角形,四边形等相关知识综合考察。所以,应该引起广大学生的重视。反比例函数中k的几何意义也是其中一块很重要的知识章节,常在中考选择题,计算大题中进行考察。这类考题大多考点简单但方法灵活,目的在于考察学生的数学图形思维。本次专题目的在于让学生掌握反比例函数k几何意义这一知识要点,灵活利用这一知识点解决数学问题,并熟悉与反比例函数k几何意义的常见考察方式和解题思路。
三、授课内容:
1.反比例函数的概念
如图所示,过双曲线上任一点作x轴、y轴的垂线
PM、PN,垂足为M、N,所得矩形PMON的面积S=PMPN=|y||x|.
∴。
这就说明,过双曲线上任意一点作x轴、y轴的垂线,所得到的矩形的面积为常数|k|。这是系数k几何意义,明确了k的几何意义,会给解题带来许多方便。(请学生思考,图中三角形OEF的面积和系数k的关系。)
2.反比例函数的图象
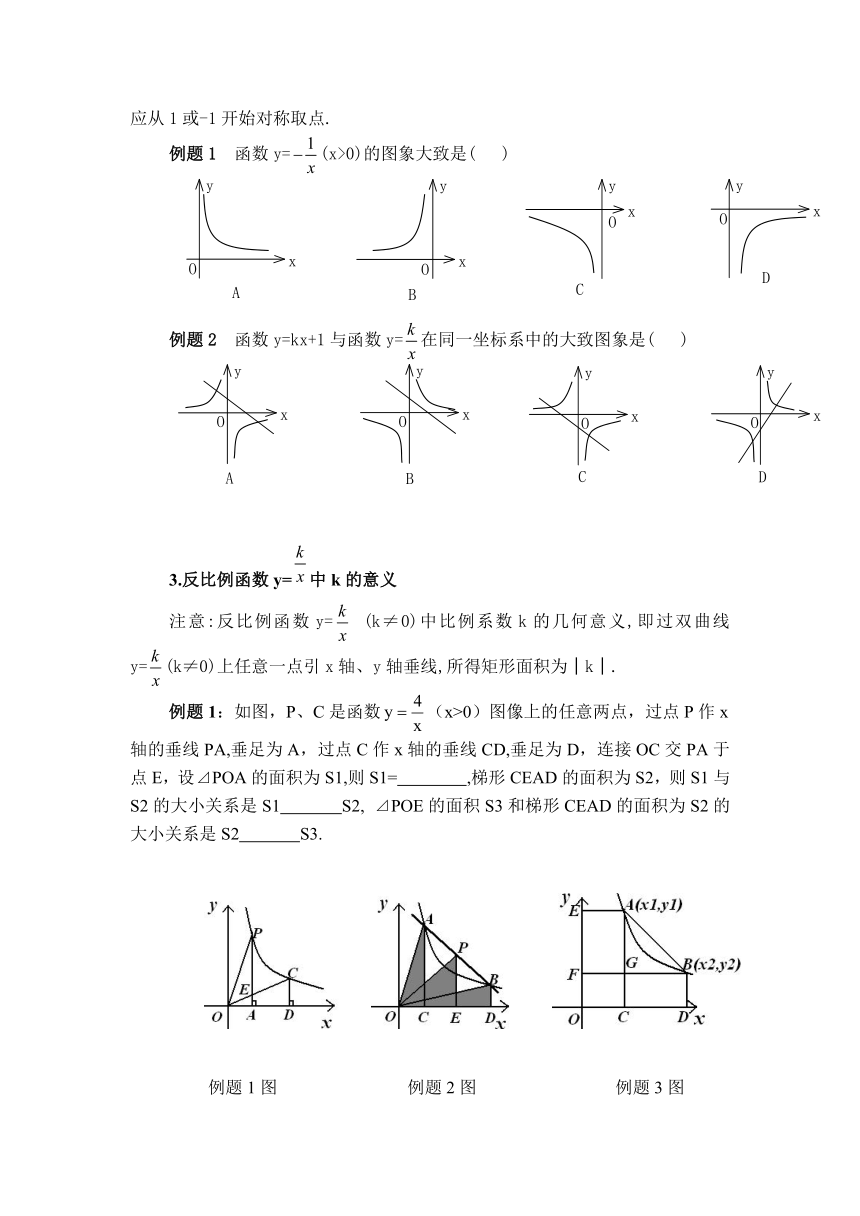
在用描点法画反比例函数y=的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.
例题1
函数y=(x>0)的图象大致是(
)
例题2
函数y=kx+1与函数y=在同一坐标系中的大致图象是(
)
3.反比例函数y=中k的意义
注意:反比例函数y=
(k≠0)中比例系数k的几何意义,即过双曲线y=(k≠0)上任意一点引x轴、y轴垂线,所得矩形面积为│k│.
例题1:如图,P、C是函数(x>0)图像上的任意两点,过点P作x轴的垂线PA,垂足为A,过点C作x轴的垂线CD,垂足为D,连接OC交PA于点E,设⊿POA的面积为S1,则S1=
,梯形CEAD的面积为S2,则S1与S2的大小关系是S1
S2,
⊿POE的面积S3和梯形CEAD的面积为S2的大小关系是S2
S3.
例题1图
例题2图
例题3图
例题2:如图所示,直线l与双曲线交A、B两点,P是AB上的点,试比较⊿AOC的面积S1,⊿BOD的面积S2,⊿POE的面积S3的大小:
。
例题3:如图所示,点A(x1,y1)、B(x2,y2)都在双曲线上,且x2-x1=4,y1-y2=2;分别过点A、B向x轴、y轴作垂线,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析式为
。
4.常考题型精选
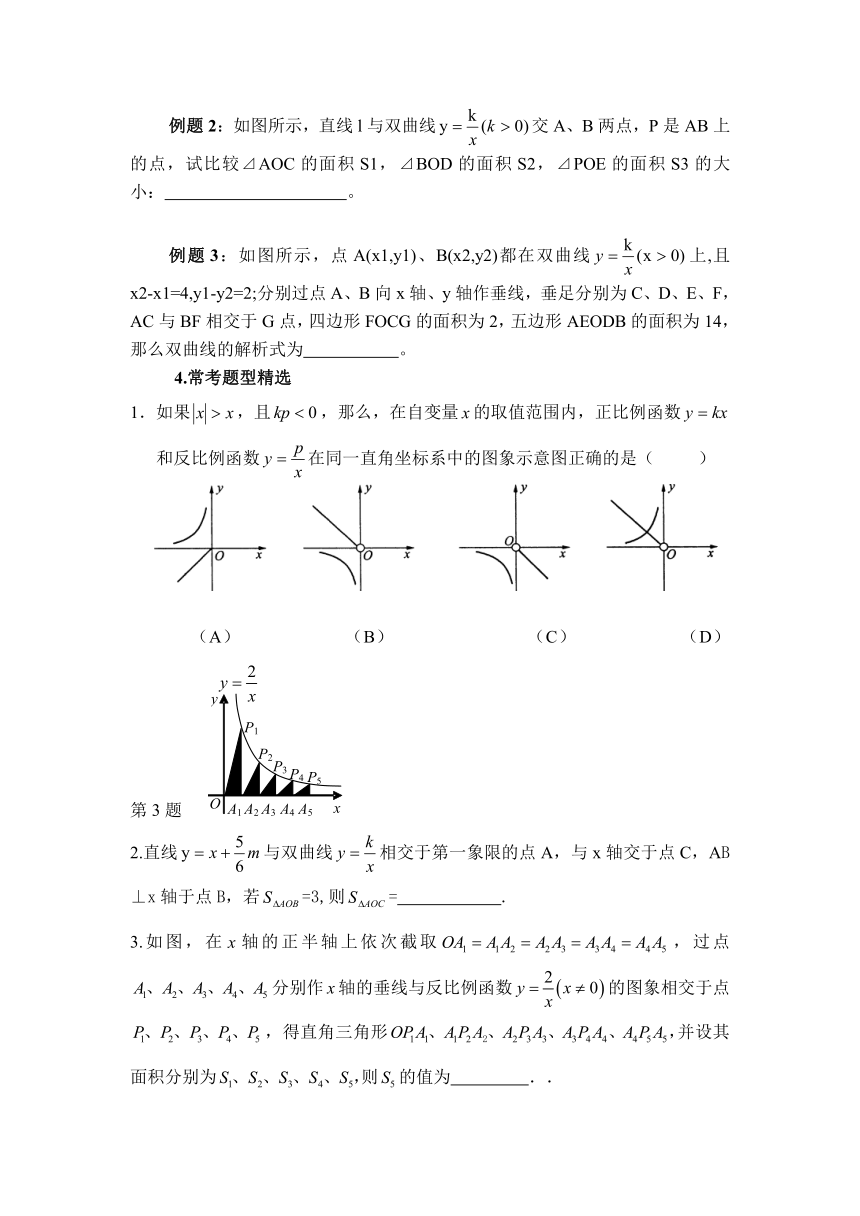
1.如果,且,那么,在自变量的取值范围内,正比例函数和反比例函数在同一直角坐标系中的图象示意图正确的是(
)
(A)
(B)
(C)
(D)
第3题
2.直线与双曲线相交于第一象限的点A,与x轴交于点C,AB⊥x轴于点B,若=3,则=
.
3.如图,在轴的正半轴上依次截取,过点分别作轴的垂线与反比例函数的图象相交于点,得直角三角形并设其面积分别为则的值为
..
4.如图,已知点A、B在双曲线上,AC⊥x轴于点C,BD⊥y轴与点D,AC与BD交于点P,P是AC的中点,若⊿ABP的面积为3,则k=
.
5.如图已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,若点A的坐标为(-6,4),则⊿AOC的面积为
。
6.如图,A、B为双曲线上的点,AD⊥x轴于D,BC⊥y轴于点C,则四边形ABCD的面积为
。
7.如图,已知双曲线经过矩形OABC边AB的中点F,交BC于点E,(1)若四边形OEBF的面积为4,
则k=
;(2)若梯形OEBA的面积为9,则k=
。
8.如图,已知双曲线经过直角三角形OAB斜边OB的中点D,与直角边AB相交与点C。若⊿OBC的面积为3,则k=
。
5.课后练习:
1.
反比例函数与一次函数只可能是(
)
(A)
(B)
(C)
(D)
第2题图
2.
正比例函数和的图象与反比例函数的图象分别相交于点和点.若和的面积分别为和,则与的关系是(
)
3.
在反比例函数()的图象上,有点,它们的横坐标依次为1,2,3,4.分别过这些点作轴与轴的垂线,图中所构成的阴影部分的面积从左到右依次为,则
.
4.反比例函数的图象所在的象限内,随增大而增大,则反比例函数的解析式是(
)
(A)
(B)
(C)
或
(D)不能确定
5.
如图9,已知正方形的面积为9,点为坐标原点,点在轴上,点在轴上,点在函数的图象上,点为其双曲线上的任一点,过点分别作轴、轴的垂线,垂足分别为、,并设矩形和正方形不重合部分的面积为.
(1)求点坐标和的值;
(2)当时,求点坐标;
(3)写出关于的函数关系式.
6.如图8,直线与反比例函数(<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(1)试确定反比例函数的关系式;
(2)求△AOC的面积.
7.如图,A、B两点在函数的图象上.(1)求的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数。
8.已知:如图,正比例函数的图象与反比例函数的图象交于点
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当取何值时,反比例函数的值大于正比例函数的值?
(3)是反比例函数图象上的一动点,其中过点作直线轴,交轴于点;过点作直线轴交轴于点,交直线于点.当四边形的面积为6时,请判断线段与的大小关系,并说明理由.
第6题
第4题
第5题
第7题
第8题
反比例函数K的几何意义
教案
一、授课目的:让学生理解反比例函数的概念及几种等价形式;能够快速绘出给定反比例函数的图像;掌握反比例函数的性质(对称性,变化趋势等),并应用解决数学问题(如比较函数值大小,求对称点坐标等)。
重点掌握反比例函数中的比例系数k的几何意义。
二、考点分析:反比例函数是历年中考数学的一个重要考点章节,且多以大题的形式出现,常常结合三角形,四边形等相关知识综合考察。所以,应该引起广大学生的重视。反比例函数中k的几何意义也是其中一块很重要的知识章节,常在中考选择题,计算大题中进行考察。这类考题大多考点简单但方法灵活,目的在于考察学生的数学图形思维。本次专题目的在于让学生掌握反比例函数k几何意义这一知识要点,灵活利用这一知识点解决数学问题,并熟悉与反比例函数k几何意义的常见考察方式和解题思路。
三、授课内容:
1.反比例函数的概念
如图所示,过双曲线上任一点作x轴、y轴的垂线
PM、PN,垂足为M、N,所得矩形PMON的面积S=PMPN=|y||x|.
∴。
这就说明,过双曲线上任意一点作x轴、y轴的垂线,所得到的矩形的面积为常数|k|。这是系数k几何意义,明确了k的几何意义,会给解题带来许多方便。(请学生思考,图中三角形OEF的面积和系数k的关系。)
2.反比例函数的图象
在用描点法画反比例函数y=的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.
例题1
函数y=(x>0)的图象大致是(
)
例题2
函数y=kx+1与函数y=在同一坐标系中的大致图象是(
)
3.反比例函数y=中k的意义
注意:反比例函数y=
(k≠0)中比例系数k的几何意义,即过双曲线y=(k≠0)上任意一点引x轴、y轴垂线,所得矩形面积为│k│.
例题1:如图,P、C是函数(x>0)图像上的任意两点,过点P作x轴的垂线PA,垂足为A,过点C作x轴的垂线CD,垂足为D,连接OC交PA于点E,设⊿POA的面积为S1,则S1=
,梯形CEAD的面积为S2,则S1与S2的大小关系是S1
S2,
⊿POE的面积S3和梯形CEAD的面积为S2的大小关系是S2
S3.
例题1图
例题2图
例题3图
例题2:如图所示,直线l与双曲线交A、B两点,P是AB上的点,试比较⊿AOC的面积S1,⊿BOD的面积S2,⊿POE的面积S3的大小:
。
例题3:如图所示,点A(x1,y1)、B(x2,y2)都在双曲线上,且x2-x1=4,y1-y2=2;分别过点A、B向x轴、y轴作垂线,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析式为
。
4.常考题型精选
1.如果,且,那么,在自变量的取值范围内,正比例函数和反比例函数在同一直角坐标系中的图象示意图正确的是(
)
(A)
(B)
(C)
(D)
第3题
2.直线与双曲线相交于第一象限的点A,与x轴交于点C,AB⊥x轴于点B,若=3,则=
.
3.如图,在轴的正半轴上依次截取,过点分别作轴的垂线与反比例函数的图象相交于点,得直角三角形并设其面积分别为则的值为
..
4.如图,已知点A、B在双曲线上,AC⊥x轴于点C,BD⊥y轴与点D,AC与BD交于点P,P是AC的中点,若⊿ABP的面积为3,则k=
.
5.如图已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,若点A的坐标为(-6,4),则⊿AOC的面积为
。
6.如图,A、B为双曲线上的点,AD⊥x轴于D,BC⊥y轴于点C,则四边形ABCD的面积为
。
7.如图,已知双曲线经过矩形OABC边AB的中点F,交BC于点E,(1)若四边形OEBF的面积为4,
则k=
;(2)若梯形OEBA的面积为9,则k=
。
8.如图,已知双曲线经过直角三角形OAB斜边OB的中点D,与直角边AB相交与点C。若⊿OBC的面积为3,则k=
。
5.课后练习:
1.
反比例函数与一次函数只可能是(
)
(A)
(B)
(C)
(D)
第2题图
2.
正比例函数和的图象与反比例函数的图象分别相交于点和点.若和的面积分别为和,则与的关系是(
)
3.
在反比例函数()的图象上,有点,它们的横坐标依次为1,2,3,4.分别过这些点作轴与轴的垂线,图中所构成的阴影部分的面积从左到右依次为,则
.
4.反比例函数的图象所在的象限内,随增大而增大,则反比例函数的解析式是(
)
(A)
(B)
(C)
或
(D)不能确定
5.
如图9,已知正方形的面积为9,点为坐标原点,点在轴上,点在轴上,点在函数的图象上,点为其双曲线上的任一点,过点分别作轴、轴的垂线,垂足分别为、,并设矩形和正方形不重合部分的面积为.
(1)求点坐标和的值;
(2)当时,求点坐标;
(3)写出关于的函数关系式.
6.如图8,直线与反比例函数(<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(1)试确定反比例函数的关系式;
(2)求△AOC的面积.
7.如图,A、B两点在函数的图象上.(1)求的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数。
8.已知:如图,正比例函数的图象与反比例函数的图象交于点
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当取何值时,反比例函数的值大于正比例函数的值?
(3)是反比例函数图象上的一动点,其中过点作直线轴,交轴于点;过点作直线轴交轴于点,交直线于点.当四边形的面积为6时,请判断线段与的大小关系,并说明理由.
第6题
第4题
第5题
第7题
第8题
