27.2.2 相似三角形的性质 教案
图片预览

文档简介
27.2.2
相似三角形的性质
教案
【知识与技能】
1.
理解并掌握相似三角形及相似多边形的周长和面积性质;
2.
能够运用相似三角形及相似多边形的周长和面积性质解决相关问题.
【过程与方法】
经历将多边形问题转化为三角形问题进行探究的过程,进一步增强学生领会转化的思想方法.
【情感态度】
通过对性质的发现和论证过程,感受数学活动中充满着探索,提高学习热情,增强探究意识.
【教学重点】
理解并能运用相似三角形及相似多边形的周长和面积性质.
【教学难点】
探索证明相似多边形面积性质的过程.
一、情境导入,初步认识
问题
(1)如果△ABC∽△,则它们之间有哪些性质?
(2)如果两个多边形相似,那么这两个多边形又有怎样的性质呢?不妨说说看,并与同伴交流.
【教学说明】以上两个问题可由学生口答,既是对前面学过知识的回顾,又是学习相似三角形及相似多边形的性质的铺垫.教师在学生回答过程中,在黑板上可写出关系式:(1)(2)
,为后面证明相似三角形及相似多边形周长的比作准备.)
二、思考探究,获取新知
问题1
你能根据刚才的性质探索出相似三角形和相似多边形周长之间各有怎样的特征?
【教学说明】让学生依据黑板上所给出的两个等式来探索新的结论,在学生自主探索过程中,教师应在黑板上画出能够相似的△ABC
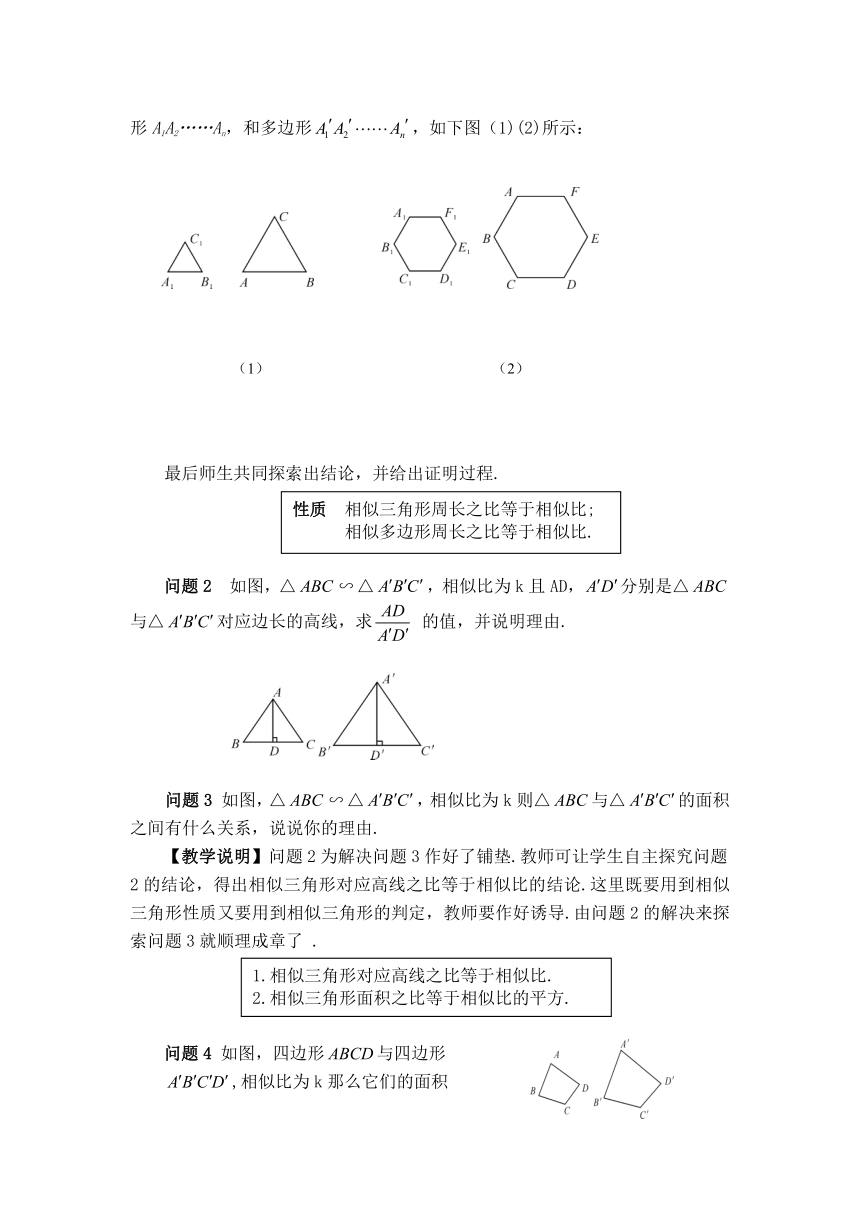
和△ABC,及相似的多边形A1A2……An,和多边形,如下图(1)(2)所示:
最后师生共同探索出结论,并给出证明过程.
问题2
如图,△△,相似比为k且AD,分别是△与△对应边长的高线,求
的值,并说明理由.
问题3
如图,△△,相似比为k则△与△的面积之间有什么关系,说说你的理由.
【教学说明】问题2为解决问题3作好了铺垫.教师可让学生自主探究问题2的结论,得出相似三角形对应高线之比等于相似比的结论.这里既要用到相似三角形性质又要用到相似三角形的判定,教师要作好诱导.由问题2的解决来探索问题3就顺理成章了
.
问题4
如图,四边形与四边形
,相似比为k那么它们的面积
之比又如何?谈谈你的看法.
【教学说明】可先让学生在小组中进行交流,
尽量找出解决问题的方法,与此同时,教师可设置
以下问题来帮助学生:你能直接表示出图中两个四边形的面积吗?如果不能,是否可连接对角线AC和AC,,用三角形的面积来表示四边形的面积呢?这样设问起到画龙点睛作用,问题便迎刃而解,最后教师可在黑板上展示说理过程,从而得出:相似四边形面积的比等于相似比的平方.
问题5
类似地,相似多边形面积之比是否也等于相似比的平方呢?
【教学说明】引导学生将两个相似多边形用类似于问题4的方法转化成若干个三角形,从而得出结论.
三、运用新知,深化理解
1.
判断:
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍.(
)
(2)—个四边形的各边长扩大为原来的9倍,它的面积扩大为原来的9倍.(
)
2.
△△,它们的周长分别为60和
72,且
AB
=15,B’C’
=24,试求
BC,AC,
A'B',A'C’
的长.
3.在一张复印出来的纸上,一个多边形的一条边由原图中2cm变成了6cm,这次复印的放缩比例是多少?这个多边形的面积发生了怎样的变化?
4.如图,在△ABC和△DEF
中,AB
=2DE,AC=2DF,A=D,△ABC的周长为
24,面积为
,求△DEF的周长和面积.
【教学说明】所选四道小题都可直接运用相似三角形和相似多边形的周长与面积性质进行判断说明,难度不大,学生可自主完成,教师巡视,发现问题,及时指导,让每个学生都学有所得.在完成上述题目后,教师引导学生完成创优作业中本课时的“名师导学”部分.
【答案】1.
(1)√
(2)×
2.BC=20,AC=25
,A’B'=18,A’C’=30.
3.这次复印的放缩比例是1:3,这个多边形的面积放大了
9倍.
四、师生互动,课堂小结
1.在探索相似多边形面积之比等于相似比的平方时,采用了怎样的思想方法,谈谈你的认识.
2.请总结一下相似三角形和相似多边形的性质.
1.布置作业:从教材P54 56习题27.
2中选取.
2.
课外思考:
(1)蛋糕店制作两种圆形蛋糕,一种半径是15cm,一种半径是30cm,如果半径为15cm的蛋糕够2个人吃,那么半径为30cm的蛋糕,够几个人吃(假设两种蛋糕的高度相同)?
(2)如图,在△ABC中,DE∥FG∥BC,
D、F在AB边上,
E、G在AC边上,且
DE、FG将△ABC的面积三等分,若
AB=10,试求AD,DF的长.
(3)完成创优作业中本课时的“课时作业”部
分.
本课时的教学过程中,首先提出问题让学生回答,这有助于学生回顾有关知识,接着教师提出问题并让学生自主探索形成初步认识,最后师生共同归纳结论.
在上述教学过程中,教师要充分调动学生的积极性,自主探究,体会发现和解决问题的乐趣.
(2)
(1)
性质
相似三角形周长之比等于相似比;
相似多边形周长之比等于相似比.
1.相似三角形对应高线之比等于相似比.
2.相似三角形面积之比等于相似比的平方.
相似多边形面积之比等于相似比的平方.
相似三角形的性质
教案
【知识与技能】
1.
理解并掌握相似三角形及相似多边形的周长和面积性质;
2.
能够运用相似三角形及相似多边形的周长和面积性质解决相关问题.
【过程与方法】
经历将多边形问题转化为三角形问题进行探究的过程,进一步增强学生领会转化的思想方法.
【情感态度】
通过对性质的发现和论证过程,感受数学活动中充满着探索,提高学习热情,增强探究意识.
【教学重点】
理解并能运用相似三角形及相似多边形的周长和面积性质.
【教学难点】
探索证明相似多边形面积性质的过程.
一、情境导入,初步认识
问题
(1)如果△ABC∽△,则它们之间有哪些性质?
(2)如果两个多边形相似,那么这两个多边形又有怎样的性质呢?不妨说说看,并与同伴交流.
【教学说明】以上两个问题可由学生口答,既是对前面学过知识的回顾,又是学习相似三角形及相似多边形的性质的铺垫.教师在学生回答过程中,在黑板上可写出关系式:(1)(2)
,为后面证明相似三角形及相似多边形周长的比作准备.)
二、思考探究,获取新知
问题1
你能根据刚才的性质探索出相似三角形和相似多边形周长之间各有怎样的特征?
【教学说明】让学生依据黑板上所给出的两个等式来探索新的结论,在学生自主探索过程中,教师应在黑板上画出能够相似的△ABC
和△ABC,及相似的多边形A1A2……An,和多边形,如下图(1)(2)所示:
最后师生共同探索出结论,并给出证明过程.
问题2
如图,△△,相似比为k且AD,分别是△与△对应边长的高线,求
的值,并说明理由.
问题3
如图,△△,相似比为k则△与△的面积之间有什么关系,说说你的理由.
【教学说明】问题2为解决问题3作好了铺垫.教师可让学生自主探究问题2的结论,得出相似三角形对应高线之比等于相似比的结论.这里既要用到相似三角形性质又要用到相似三角形的判定,教师要作好诱导.由问题2的解决来探索问题3就顺理成章了
.
问题4
如图,四边形与四边形
,相似比为k那么它们的面积
之比又如何?谈谈你的看法.
【教学说明】可先让学生在小组中进行交流,
尽量找出解决问题的方法,与此同时,教师可设置
以下问题来帮助学生:你能直接表示出图中两个四边形的面积吗?如果不能,是否可连接对角线AC和AC,,用三角形的面积来表示四边形的面积呢?这样设问起到画龙点睛作用,问题便迎刃而解,最后教师可在黑板上展示说理过程,从而得出:相似四边形面积的比等于相似比的平方.
问题5
类似地,相似多边形面积之比是否也等于相似比的平方呢?
【教学说明】引导学生将两个相似多边形用类似于问题4的方法转化成若干个三角形,从而得出结论.
三、运用新知,深化理解
1.
判断:
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍.(
)
(2)—个四边形的各边长扩大为原来的9倍,它的面积扩大为原来的9倍.(
)
2.
△△,它们的周长分别为60和
72,且
AB
=15,B’C’
=24,试求
BC,AC,
A'B',A'C’
的长.
3.在一张复印出来的纸上,一个多边形的一条边由原图中2cm变成了6cm,这次复印的放缩比例是多少?这个多边形的面积发生了怎样的变化?
4.如图,在△ABC和△DEF
中,AB
=2DE,AC=2DF,A=D,△ABC的周长为
24,面积为
,求△DEF的周长和面积.
【教学说明】所选四道小题都可直接运用相似三角形和相似多边形的周长与面积性质进行判断说明,难度不大,学生可自主完成,教师巡视,发现问题,及时指导,让每个学生都学有所得.在完成上述题目后,教师引导学生完成创优作业中本课时的“名师导学”部分.
【答案】1.
(1)√
(2)×
2.BC=20,AC=25
,A’B'=18,A’C’=30.
3.这次复印的放缩比例是1:3,这个多边形的面积放大了
9倍.
四、师生互动,课堂小结
1.在探索相似多边形面积之比等于相似比的平方时,采用了怎样的思想方法,谈谈你的认识.
2.请总结一下相似三角形和相似多边形的性质.
1.布置作业:从教材P54 56习题27.
2中选取.
2.
课外思考:
(1)蛋糕店制作两种圆形蛋糕,一种半径是15cm,一种半径是30cm,如果半径为15cm的蛋糕够2个人吃,那么半径为30cm的蛋糕,够几个人吃(假设两种蛋糕的高度相同)?
(2)如图,在△ABC中,DE∥FG∥BC,
D、F在AB边上,
E、G在AC边上,且
DE、FG将△ABC的面积三等分,若
AB=10,试求AD,DF的长.
(3)完成创优作业中本课时的“课时作业”部
分.
本课时的教学过程中,首先提出问题让学生回答,这有助于学生回顾有关知识,接着教师提出问题并让学生自主探索形成初步认识,最后师生共同归纳结论.
在上述教学过程中,教师要充分调动学生的积极性,自主探究,体会发现和解决问题的乐趣.
(2)
(1)
性质
相似三角形周长之比等于相似比;
相似多边形周长之比等于相似比.
1.相似三角形对应高线之比等于相似比.
2.相似三角形面积之比等于相似比的平方.
相似多边形面积之比等于相似比的平方.
