河南省郑州市2016-2017学年九年级(上)开学数学试卷(解析版)
文档属性
| 名称 | 河南省郑州市2016-2017学年九年级(上)开学数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 218.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 00:00:00 | ||
图片预览




文档简介
2016-2017学年河南省郑州市九年级(上)开学数学试卷
一、选择题(共8小题,每小题3分,满分24分)
1.用配方法解一元二次方程x2+4x﹣3=0时,原方程可变形为( )
A.(x+2)2=1
B.(x+2)2=7
C.(x+2)2=13
D.(x+2)2=19
2.下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
3.下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )
A.
B.
C.
D.
4.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=( )
A.
B.
C.
D.1
5.若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5
B.k<5,且k≠1
C.k≤5,且k≠1
D.k>5
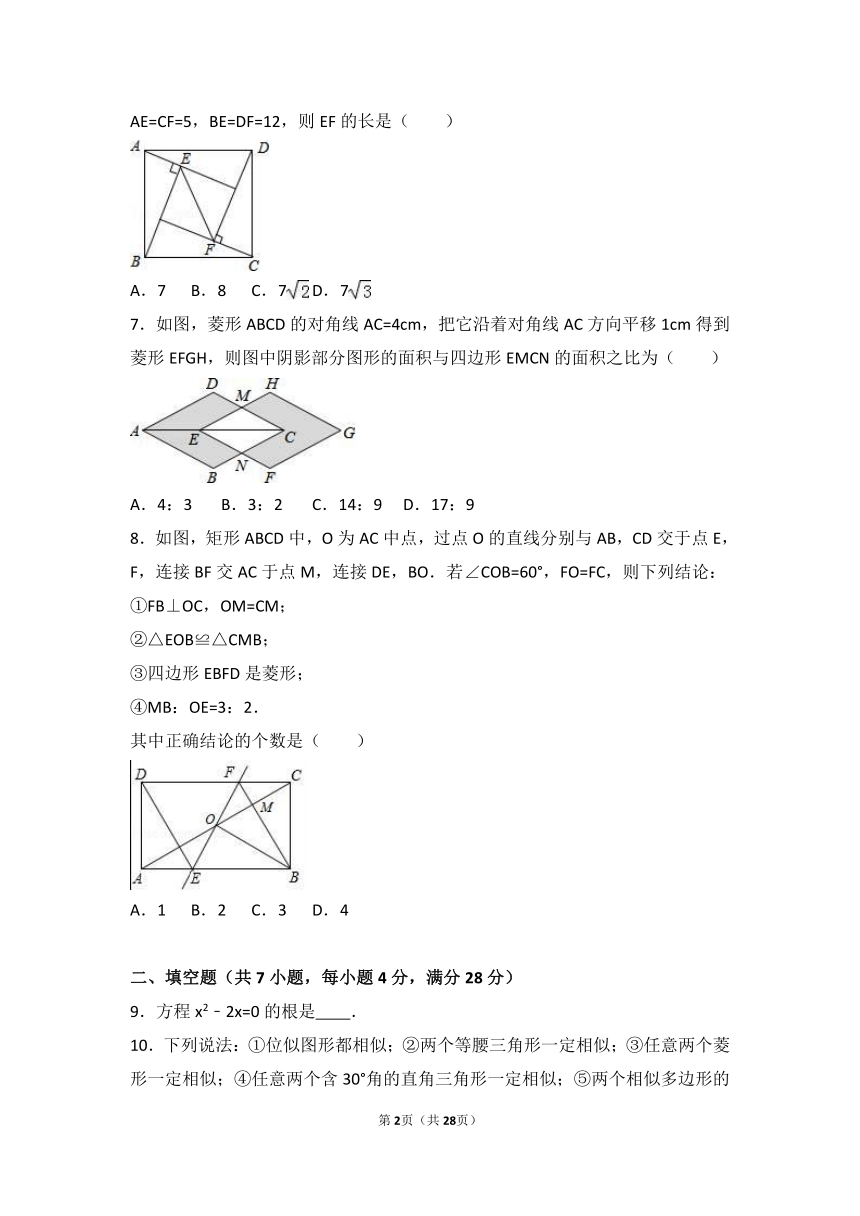
6.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
A.7
B.8
C.7
D.7
7.如图,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为( )
A.4:3
B.3:2
C.14:9
D.17:9
8.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:
①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
二、填空题(共7小题,每小题4分,满分28分)
9.方程x2﹣2x=0的根是 .
10.下列说法:①位似图形都相似;②两个等腰三角形一定相似;③任意两个菱形一定相似;④任意两个含30°角的直角三角形一定相似;⑤两个相似多边形的面积比为4:9,则周长比为16:81;⑥若一个三角形的三边分别比另一个三角形的三边长2cm,则这两个三角形一定相似.其中正确的说法有 (填写序号).
11.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF= .
12.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为 .
13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球标号的积小于4的概率是 .
14.如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3),x反比例函数y=的图象与菱形对角线AO交于点D,连接BD,当BD⊥x轴时,k的值是 .
15.如图,在四边形ABCD中,DC∥AB,AD=4,DC=5,AB=8.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为每秒1个单位长度.当P点到达C点时,两点同时停止运动,连接PQ.设运动时间为t秒,当△PQB为等腰三角形时,t的值为 .
三、解答题(共5小题,满分48分)
16.如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,
AE=CF.
(1)求证:△ABF≌△CDE;
(2)当四边形ABCD满足什么条件时,四边形BFDE是菱形?为什么?
17.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
18.如图,在平面直角坐标系中,一次函数y=ax+b的图象于反比例函数y=的图象相交于点A(﹣4,﹣2),B(m,4),与y轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)观察函数图象,直接写出一次函数图象在反比例函数图象上方时,自变量x的取值范围.
19.某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销,购进价格为每件10元,若售价为12元/件,则可全部售出;若每涨价0.1元,销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少m%.结果10月份利润达到3300元,求m的值(m>0).
20.在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
特殊发现:
如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:
把图1中的△AEF绕着点A顺时针旋转.
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
2016-2017学年河南省郑州市九年级(上)开学数学试卷
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.用配方法解一元二次方程x2+4x﹣3=0时,原方程可变形为( )
A.(x+2)2=1
B.(x+2)2=7
C.(x+2)2=13
D.(x+2)2=19
【考点】解一元二次方程-配方法.
【分析】把方程两边加上7,然后把方程左边写成完全平方式即可.
【解答】解:x2+4x=3,
x2+4x+4=7,
(x+2)2=7.
故选B.
2.下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
【考点】概率的意义.
【分析】根据概率的意义对各选项进行逐一分析即可.
【解答】解:A、袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球的概率是,故本选项错误;
B、天气预报“明天降水概率10%”,是指明天有10%的概率会下雨,故本选项错误;
C、某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,可能会中奖,故本选项错误;
D、连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上,故本选项正确.
故选D.
3.下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )
A.
B.
C.
D.
【考点】简单几何体的三视图.
【分析】首先判断几何体的三视图,然后找到答案即可.
【解答】解:几何体的主视图为选项D,俯视图为选项B,左视图为选项C.
故选A.
4.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=( )
A.
B.
C.
D.1
【考点】平行线分线段成比例.
【分析】直接根据平行线分线段成比例定理求解.
【解答】解:∵a∥b∥c,
∴==.
故选B.
5.若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5
B.k<5,且k≠1
C.k≤5,且k≠1
D.k>5
【考点】根的判别式;一元二次方程的定义.
【分析】根据方程为一元二次方程且有两个不相等的实数根,结合一元二次方程的定义以及根的判别式即可得出关于k的一元一次不等式组,解不等式组即可得出结论.
【解答】解:∵关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,
∴,即,
解得:k<5且k≠1.
故选B.
6.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
A.7
B.8
C.7
D.7
【考点】正方形的性质.
【分析】由正方形的性质得出∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,由SSS证明△ABE≌△CDF,得出∠ABE=∠CDF,证出∠ABE=∠DAG=∠CDF=∠BCH,由AAS证明△ABE≌△ADG,得出AE=DG,BE=AG,同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,得出EG=GF=FH=EF=7,证出四边形EGFH是正方形,即可得出结果.
【解答】解:如图所示:
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,
∴∠BAE+∠DAG=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SSS),
∴∠ABE=∠CDF,
∵∠AEB=∠CFD=90°,
∴∠ABE+∠BAE=90°,
∴∠ABE=∠DAG=∠CDF,
同理:∠ABE=∠DAG=∠CDF=∠BCH,
∴∠DAG+∠ADG=∠CDF+∠ADG=90°,
即∠DGA=90°,
同理:∠CHB=90°,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(AAS),
∴AE=DG,BE=AG,
同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,
∴EG=GF=FH=EF=12﹣5=7,
∵∠GEH=180°﹣90°=90°,
∴四边形EGFH是正方形,
∴EF=EG=7;
故选:C.
7.如图,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为( )
A.4:3
B.3:2
C.14:9
D.17:9
【考点】菱形的性质;平移的性质.
【分析】首先得出△MEC∽△DAC,则=,进而得出=,即可得出答案.
【解答】解:∵ME∥AD,
∴△MEC∽△DAC,
∴=,
∵菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,
∴AE=1cm,EC=3cm,
∴=,
∴=,
∴图中阴影部分图形的面积与四边形EMCN的面积之比为:
=.
故选:C.
8.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:
①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【考点】菱形的判定与性质;全等三角形的判定与性质;矩形的性质.
【分析】①根据已知得出△OBF≌△CBF,可求得△OBF与△CBF关于直线BF对称,进而求得FB⊥OC,OM=CM;
②因为△EOB≌△FOB≌△FCB,故△EOB不会全等于△CBM.
③先证得∠ABO=∠OBF=30°,再证得OE=OF,进而证得OB⊥EF,因为BD、EF互相平分,即可证得四边形EBFD是菱形;
④根据三角函数求得MB=,OF=,根据OE=OF即可求得MB:OE=3:2.
【解答】解:连接BD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM;
∴①正确,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
∵OA=OC,
易证△AOE≌△COF,
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
∵△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴②错误,
∵∠OMB=∠BOF=90°,∠OBF=30°,
∴MB=,OF=,
∵OE=OF,
∴MB:OE=3:2,
∴④正确;
故选:C.
二、填空题(共7小题,每小题4分,满分28分)
9.方程x2﹣2x=0的根是 x1=0,x2=2 .
【考点】解一元二次方程-因式分解法.
【分析】因为x2﹣2x可提取公因式,故用因式分解法解较简便.
【解答】解:因式分解得x(x﹣2)=0,
解得x1=0,x2=2.
故答案为x1=0,x2=2.
10.下列说法:①位似图形都相似;②两个等腰三角形一定相似;③任意两个菱形一定相似;④任意两个含30°角的直角三角形一定相似;⑤两个相似多边形的面积比为4:9,则周长比为16:81;⑥若一个三角形的三边分别比另一个三角形的三边长2cm,则这两个三角形一定相似.其中正确的说法有 ①④ (填写序号).
【考点】位似变换;等腰三角形的性质;含30度角的直角三角形;菱形的性质;相似多边形的性质;相似三角形的判定.
【分析】根据位似的性质对①进行判断;根据相似三角形的判定方法与反例对②⑥进行判断;根据内角不为90的菱形与内角为90的菱形不相似对③进行判断;根据相似三角形的性质对⑤进行判断.
【解答】解:位似图形都相似,所以①正确;
两个等腰三角形不一定相似,如等边三角形与等腰直角三角形不相似,所以②错误;
任意两个菱形不一定相似,所以③错误;
任意两个含30°角的直角三角形一定相似,所以④正确;
两个相似多边形的面积比为4:9,则周长比为2:3,所以⑤错误;
若一个三角形的三边分别比另一个三角形的三边长2cm,则这两个三角形不一定相似,若边长为3、4、5的三角形与边长为5、6、7的三角形不相似,所以⑥错误.
故答案为①④.
11.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF= .
【考点】翻折变换(折叠问题);矩形的性质.
【分析】先求得∠ABD=60°,由翻折的性质可得到∠ABE=120°,于是可求得∠FBE=30°,最后依据特殊锐角三角函数值可求得EF的长.
【解答】解:∵∠ADB=30°,∠BAD=90°,
∴∠ABD=60°.
∵由翻折的性质可知:∠ABE=120°,AB=BE=3,∠E=∠A=90°,
∴∠FBE=30°.
∴==,
解得:EF=.
故答案为:.
12.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为 .
【考点】菱形的性质.
【分析】如图,连接BD交AC于E,由四边形ABCD是菱形,推出AC⊥BD,AE=EC,在Rt△EOD中,利用勾股定理求出DE,在Rt△ADE中利用勾股定理求出AD即可.
【解答】解:如图,连接BD交AC于E.
∵四边形ABCD是菱形,
∴AC⊥BD,AE=EC,
∵OA=2OC,AC=3,
∴CO=DO=2EO=1,AE=,
∴EO=,DE=EB===,
∴AD===.
故答案为.
13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球标号的积小于4的概率是 .
【考点】列表法与树状图法.
【分析】画树状图展示所有6种等可能的结果数,再找出两次摸出的小球标号的积小于4的结果数,然后根据概率公式求解.
【解答】解:画树状图为:
共有12种等可能的结果数,其中两次摸出的小球标号的积小于4的结果数为4,
所以两次摸出的小球标号的积小于4的概率==.
故答案为.
14.如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3),x反比例函数y=的图象与菱形对角线AO交于点D,连接BD,当BD⊥x轴时,k的值是 ﹣12 .
【考点】菱形的性质;反比例函数图象上点的坐标特征.
【分析】延长AC交y轴于E,如图,根据菱形的性质得AC∥OB,则AE⊥y轴,再由∠BOC=60°得到∠COE=30°,则根据含30度的直角三角形三边的关系得到CE=OE=3,OC=2CE=6,接着根据菱形的性质得OB=OC=6,∠BOA=30°,于是在Rt△BDO中可计算出BD=OB=2,所以D点坐标为(﹣6,2),然后利用反比例函数图象上点的坐标特征可求出k的值.
【解答】解:延长AC交y轴于E,如图,
∵菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,
∴AC∥OB,
∴AE⊥y轴,
∵∠BOC=60°,
∴∠COE=30°,
而顶点C的坐标为(m,3),
∴OE=3,
∴CE=OE=3,
∴OC=2CE=6,
∵四边形ABOC为菱形,
∴OB=OC=6,∠BOA=30°,
在Rt△BDO中,
∵BD=OB=2,
∴D点坐标为(﹣6,2),
∵反比例函数y=的图象经过点D,
∴k=﹣6×2=﹣12.
故答案为﹣12.
15.如图,在四边形ABCD中,DC∥AB,AD=4,DC=5,AB=8.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为每秒1个单位长度.当P点到达C点时,两点同时停止运动,连接PQ.设运动时间为t秒,当△PQB为等腰三角形时,t的值为 、或4 .
【考点】相似三角形的判定与性质;等腰三角形的性质.
【分析】根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
【解答】解:如图1,作CE⊥AB于E,
∵DC∥AB,DA⊥AB,
∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4,
∴BE=3,
∴BC==5,
cos∠B=,
①当PQ=PB时(如图2所示),则BG=BQ,
==,
解得:t=s,
②当PQ=BQ时(如图3所示),则BG=PB,
==,
解得t=s,
③当BP=BQ时(如图4所示),则8﹣t=t,
解得:t=4.
综上所述:当t=s,
s或t=4s时,△PQB为等腰三角形.
故答案为:、或4.
三、解答题(共5小题,满分48分)
16.如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,
AE=CF.
(1)求证:△ABF≌△CDE;
(2)当四边形ABCD满足什么条件时,四边形BFDE是菱形?为什么?
【考点】菱形的判定;全等三角形的判定与性质.
【分析】(1)由平行线的性质得出∠BAC=∠DCA.证出AF=CE.由AAS证明△ABF≌△CDE即可;
(2)先证明四边形ABCD是菱形,得出BD⊥AC,再证明四边形BFDE是平行四边形,即可得出结论.
【解答】(1)证明:∵AB∥CD,
∴∠BAC=∠DCA.
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△ABF和△CDE中,
,
又∵∠ABF=∠CDE,
∴△ABF≌△CDE(AAS);
(2)解:当四边形ABCD满足AB=AD时,四边形BEDF是菱形.理由如下:
连接BD交AC于点O,如图所示:
由(1)得:△ABF≌△CDE,
∴AB=CD,BF=DE,∠AFB=∠CED,
∴BF∥DE.
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴平行四边形ABCD是菱形.
∴BD⊥AC.
∵BF=DE,BF∥DE,
∴四边形BEDF是平行四边形,
∴四边形BEDF是菱形.
17.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
【考点】根的判别式;等腰三角形的判定;勾股定理的逆定理.
【分析】(1)根据方程解的定义把x=﹣1代入方程得到(a+c)×(﹣1)2﹣2b+(a﹣c)=0,整理得a﹣b=0,即a=b,于是根据等腰三角形的判定即可得到△ABC是等腰三角形;
(2)根据判别式的意义得到△=(2b)2﹣4(a+c)(a﹣c)=0,整理得a2=b2+c2,然后根据勾股定理的逆定理得到△ABC是直角三角形.
【解答】解:(1)△ABC是等腰三角形.理由如下:
∵x=﹣1是方程的根,
∴(a+c)×(﹣1)2﹣2b+(a﹣c)=0,
∴a+c﹣2b+a﹣c=0,
∴a﹣b=0,
∴a=b,
∴△ABC是等腰三角形;
(2)△ABC是直角三角形.理由如下:
∵方程有两个相等的实数根,
∴△=(2b)2﹣4(a+c)(a﹣c)=0,
∴4b2﹣4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形.
18.如图,在平面直角坐标系中,一次函数y=ax+b的图象于反比例函数y=的图象相交于点A(﹣4,﹣2),B(m,4),与y轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)观察函数图象,直接写出一次函数图象在反比例函数图象上方时,自变量x的取值范围.
【考点】反比例函数与一次函数的交点问题.
【分析】(1)把A(﹣4,﹣2)代入y=求出看,即可得出反比例函数的表达式,把B(m,4)代入y=求出B的坐标,把A、B的坐标代入y=kx+b得出,求出k、b,即可求出一次函数的表达式;
(2)把x=0代入y=x+2求出OC,分别求出△AOC和△BOC的面积,相加即可;
(3)根据A、B的坐标和图象得出即可.
【解答】解:(1)把A(﹣4,﹣2)代入y=得:k=8,
即反比例函数的表达式为y=,
把B(m,4)代入y=得:4=,
解得:m=2,
即B(2,4),
把A、B的坐标代入y=kx+b得:,
解得:k=1,b=2,
即一次函数的表达式为y=x+2;
(2)把x=0代入y=x+2得:y=2,
即OC=2,
所以△AOB的面积为:×2×|﹣4|+×2×2=6;
(3)由图象可知:一次函数图象在反比例函数图象上方时,自变量x的取值范围是x>2或﹣4<x<0.
19.某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销,购进价格为每件10元,若售价为12元/件,则可全部售出;若每涨价0.1元,销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少m%.结果10月份利润达到3300元,求m的值(m>0).
【考点】一元二次方程的应用;一元一次不等式的应用.
【分析】(1)设售价应为x元,根据不等关系:该文具店在9月份销售量不低于1100件,列出不等式求解即可;
(2)先求出10月份的进价,再根据等量关系:10月份利润达到3300元,列出方程求解即可.
【解答】解:(1)设售价应为x元,依题意有
1160﹣≥1100,
解得:x≤15.
答:售价应不高于15元.
(2)10月份的进价:10(1+20%)=12(元),
由题意得:
1100(1+m%)[15(1﹣m%)﹣12]=3300,
设m%=t,化简得2t2﹣t=0,
解得:t1=0,t2=0.5,
所以m1=0,m2=50%,
因为m>0,
所以m=50.
答:m的值为50.
20.在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
特殊发现:
如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:
把图1中的△AEF绕着点A顺时针旋转.
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
【考点】几何变换综合题.
【分析】(1)首先过点P作PM⊥CE于点M,然后根据EF⊥AE,BC⊥AC,可得EF∥MP∥CB,推得,再根据点P是BF的中点,可得EM=MC,据此推得PC=PE即可.
(2)首先过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,然后根据全等三角形判定的方法,判断出△DAF≌△EAF,即可判断出AD=AE;再判断出△DAP≌△EAP,即可判断出PD=PE;最后根据FD⊥AC,BC⊥AC,PM⊥AC,可得FD∥BC∥PM,再根据点P是BF的中点,推得PC=PD,再根据PD=PE,即可推得PC=PE.
(3)首先根据△CPE总是等边三角形,可得将△AEF绕着点A顺时针旋转180°,△CPE仍是等边三角形;然后根据∠BCF=∠BEF=90°,点P是BF的中点,可得点C、E在以点P为圆心,BF为直径的圆上;最后根据圆周角定理,求出∠CBE的度数,即可求出当△CPE总是等边三角形时,k的值是多少.
【解答】解:(1)如图2,过点P作PM⊥CE于点M,
,
PC=PE成立,理由如下:
∵EF⊥AE,BC⊥AC,
∴EF∥MP∥CB,
∴,
∵点P是BF的中点,
∴EM=MC,
又∵PM⊥CE,
∴PC=PE.
(2)如图3,过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,
,
PC=PE成立,理由如下:
∵∠DAF=∠EAF,∠FDA=∠FEA=90°,
在△DAF和△EAF中,
,
∴△DAF≌△EAF(AAS),
∴AD=AE,
在△DAP和△EAP中,
,
∴△DAP≌△EAP(SAS),
∴PD=PE,
∵FD⊥AC,BC⊥AC,PM⊥AC,
∴FD∥BC∥PM,
∴,
∵点P是BF的中点,
∴DM=MC,
又∵PM⊥AC,
∴PC=PD,
又∵PD=PE,
∴PC=PE.
(3)如图4,,
∵△CPE总是等边三角形,
∴将△AEF绕着点A顺时针旋转180°,△CPE仍是等边三角形,
∵∠BCF=∠BEF=90°,点P是BF的中点,
∴点C、E在以点P为圆心,BF为直径的圆上,
∵△CPE是等边三角形,
∴∠CPE=60°,
根据圆周角定理,可得
∠CBE=∠CPE=60°=30°,
即∠ABC=30°,
在Rt△ABC中,
∵=k,
=tan30°,
∴k=tan30°=,
∴当k为时,△CPE总是等边三角形.
2017年2月21日
第1页(共28页)
一、选择题(共8小题,每小题3分,满分24分)
1.用配方法解一元二次方程x2+4x﹣3=0时,原方程可变形为( )
A.(x+2)2=1
B.(x+2)2=7
C.(x+2)2=13
D.(x+2)2=19
2.下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
3.下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )
A.
B.
C.
D.
4.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=( )
A.
B.
C.
D.1
5.若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5
B.k<5,且k≠1
C.k≤5,且k≠1
D.k>5
6.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
A.7
B.8
C.7
D.7
7.如图,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为( )
A.4:3
B.3:2
C.14:9
D.17:9
8.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:
①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
二、填空题(共7小题,每小题4分,满分28分)
9.方程x2﹣2x=0的根是 .
10.下列说法:①位似图形都相似;②两个等腰三角形一定相似;③任意两个菱形一定相似;④任意两个含30°角的直角三角形一定相似;⑤两个相似多边形的面积比为4:9,则周长比为16:81;⑥若一个三角形的三边分别比另一个三角形的三边长2cm,则这两个三角形一定相似.其中正确的说法有 (填写序号).
11.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF= .
12.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为 .
13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球标号的积小于4的概率是 .
14.如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3),x反比例函数y=的图象与菱形对角线AO交于点D,连接BD,当BD⊥x轴时,k的值是 .
15.如图,在四边形ABCD中,DC∥AB,AD=4,DC=5,AB=8.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为每秒1个单位长度.当P点到达C点时,两点同时停止运动,连接PQ.设运动时间为t秒,当△PQB为等腰三角形时,t的值为 .
三、解答题(共5小题,满分48分)
16.如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,
AE=CF.
(1)求证:△ABF≌△CDE;
(2)当四边形ABCD满足什么条件时,四边形BFDE是菱形?为什么?
17.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
18.如图,在平面直角坐标系中,一次函数y=ax+b的图象于反比例函数y=的图象相交于点A(﹣4,﹣2),B(m,4),与y轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)观察函数图象,直接写出一次函数图象在反比例函数图象上方时,自变量x的取值范围.
19.某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销,购进价格为每件10元,若售价为12元/件,则可全部售出;若每涨价0.1元,销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少m%.结果10月份利润达到3300元,求m的值(m>0).
20.在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
特殊发现:
如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:
把图1中的△AEF绕着点A顺时针旋转.
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
2016-2017学年河南省郑州市九年级(上)开学数学试卷
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.用配方法解一元二次方程x2+4x﹣3=0时,原方程可变形为( )
A.(x+2)2=1
B.(x+2)2=7
C.(x+2)2=13
D.(x+2)2=19
【考点】解一元二次方程-配方法.
【分析】把方程两边加上7,然后把方程左边写成完全平方式即可.
【解答】解:x2+4x=3,
x2+4x+4=7,
(x+2)2=7.
故选B.
2.下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
【考点】概率的意义.
【分析】根据概率的意义对各选项进行逐一分析即可.
【解答】解:A、袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球的概率是,故本选项错误;
B、天气预报“明天降水概率10%”,是指明天有10%的概率会下雨,故本选项错误;
C、某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,可能会中奖,故本选项错误;
D、连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上,故本选项正确.
故选D.
3.下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )
A.
B.
C.
D.
【考点】简单几何体的三视图.
【分析】首先判断几何体的三视图,然后找到答案即可.
【解答】解:几何体的主视图为选项D,俯视图为选项B,左视图为选项C.
故选A.
4.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=( )
A.
B.
C.
D.1
【考点】平行线分线段成比例.
【分析】直接根据平行线分线段成比例定理求解.
【解答】解:∵a∥b∥c,
∴==.
故选B.
5.若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5
B.k<5,且k≠1
C.k≤5,且k≠1
D.k>5
【考点】根的判别式;一元二次方程的定义.
【分析】根据方程为一元二次方程且有两个不相等的实数根,结合一元二次方程的定义以及根的判别式即可得出关于k的一元一次不等式组,解不等式组即可得出结论.
【解答】解:∵关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,
∴,即,
解得:k<5且k≠1.
故选B.
6.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
A.7
B.8
C.7
D.7
【考点】正方形的性质.
【分析】由正方形的性质得出∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,由SSS证明△ABE≌△CDF,得出∠ABE=∠CDF,证出∠ABE=∠DAG=∠CDF=∠BCH,由AAS证明△ABE≌△ADG,得出AE=DG,BE=AG,同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,得出EG=GF=FH=EF=7,证出四边形EGFH是正方形,即可得出结果.
【解答】解:如图所示:
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,
∴∠BAE+∠DAG=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SSS),
∴∠ABE=∠CDF,
∵∠AEB=∠CFD=90°,
∴∠ABE+∠BAE=90°,
∴∠ABE=∠DAG=∠CDF,
同理:∠ABE=∠DAG=∠CDF=∠BCH,
∴∠DAG+∠ADG=∠CDF+∠ADG=90°,
即∠DGA=90°,
同理:∠CHB=90°,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(AAS),
∴AE=DG,BE=AG,
同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,
∴EG=GF=FH=EF=12﹣5=7,
∵∠GEH=180°﹣90°=90°,
∴四边形EGFH是正方形,
∴EF=EG=7;
故选:C.
7.如图,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为( )
A.4:3
B.3:2
C.14:9
D.17:9
【考点】菱形的性质;平移的性质.
【分析】首先得出△MEC∽△DAC,则=,进而得出=,即可得出答案.
【解答】解:∵ME∥AD,
∴△MEC∽△DAC,
∴=,
∵菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,
∴AE=1cm,EC=3cm,
∴=,
∴=,
∴图中阴影部分图形的面积与四边形EMCN的面积之比为:
=.
故选:C.
8.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:
①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【考点】菱形的判定与性质;全等三角形的判定与性质;矩形的性质.
【分析】①根据已知得出△OBF≌△CBF,可求得△OBF与△CBF关于直线BF对称,进而求得FB⊥OC,OM=CM;
②因为△EOB≌△FOB≌△FCB,故△EOB不会全等于△CBM.
③先证得∠ABO=∠OBF=30°,再证得OE=OF,进而证得OB⊥EF,因为BD、EF互相平分,即可证得四边形EBFD是菱形;
④根据三角函数求得MB=,OF=,根据OE=OF即可求得MB:OE=3:2.
【解答】解:连接BD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM;
∴①正确,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
∵OA=OC,
易证△AOE≌△COF,
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
∵△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴②错误,
∵∠OMB=∠BOF=90°,∠OBF=30°,
∴MB=,OF=,
∵OE=OF,
∴MB:OE=3:2,
∴④正确;
故选:C.
二、填空题(共7小题,每小题4分,满分28分)
9.方程x2﹣2x=0的根是 x1=0,x2=2 .
【考点】解一元二次方程-因式分解法.
【分析】因为x2﹣2x可提取公因式,故用因式分解法解较简便.
【解答】解:因式分解得x(x﹣2)=0,
解得x1=0,x2=2.
故答案为x1=0,x2=2.
10.下列说法:①位似图形都相似;②两个等腰三角形一定相似;③任意两个菱形一定相似;④任意两个含30°角的直角三角形一定相似;⑤两个相似多边形的面积比为4:9,则周长比为16:81;⑥若一个三角形的三边分别比另一个三角形的三边长2cm,则这两个三角形一定相似.其中正确的说法有 ①④ (填写序号).
【考点】位似变换;等腰三角形的性质;含30度角的直角三角形;菱形的性质;相似多边形的性质;相似三角形的判定.
【分析】根据位似的性质对①进行判断;根据相似三角形的判定方法与反例对②⑥进行判断;根据内角不为90的菱形与内角为90的菱形不相似对③进行判断;根据相似三角形的性质对⑤进行判断.
【解答】解:位似图形都相似,所以①正确;
两个等腰三角形不一定相似,如等边三角形与等腰直角三角形不相似,所以②错误;
任意两个菱形不一定相似,所以③错误;
任意两个含30°角的直角三角形一定相似,所以④正确;
两个相似多边形的面积比为4:9,则周长比为2:3,所以⑤错误;
若一个三角形的三边分别比另一个三角形的三边长2cm,则这两个三角形不一定相似,若边长为3、4、5的三角形与边长为5、6、7的三角形不相似,所以⑥错误.
故答案为①④.
11.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF= .
【考点】翻折变换(折叠问题);矩形的性质.
【分析】先求得∠ABD=60°,由翻折的性质可得到∠ABE=120°,于是可求得∠FBE=30°,最后依据特殊锐角三角函数值可求得EF的长.
【解答】解:∵∠ADB=30°,∠BAD=90°,
∴∠ABD=60°.
∵由翻折的性质可知:∠ABE=120°,AB=BE=3,∠E=∠A=90°,
∴∠FBE=30°.
∴==,
解得:EF=.
故答案为:.
12.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为 .
【考点】菱形的性质.
【分析】如图,连接BD交AC于E,由四边形ABCD是菱形,推出AC⊥BD,AE=EC,在Rt△EOD中,利用勾股定理求出DE,在Rt△ADE中利用勾股定理求出AD即可.
【解答】解:如图,连接BD交AC于E.
∵四边形ABCD是菱形,
∴AC⊥BD,AE=EC,
∵OA=2OC,AC=3,
∴CO=DO=2EO=1,AE=,
∴EO=,DE=EB===,
∴AD===.
故答案为.
13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球标号的积小于4的概率是 .
【考点】列表法与树状图法.
【分析】画树状图展示所有6种等可能的结果数,再找出两次摸出的小球标号的积小于4的结果数,然后根据概率公式求解.
【解答】解:画树状图为:
共有12种等可能的结果数,其中两次摸出的小球标号的积小于4的结果数为4,
所以两次摸出的小球标号的积小于4的概率==.
故答案为.
14.如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3),x反比例函数y=的图象与菱形对角线AO交于点D,连接BD,当BD⊥x轴时,k的值是 ﹣12 .
【考点】菱形的性质;反比例函数图象上点的坐标特征.
【分析】延长AC交y轴于E,如图,根据菱形的性质得AC∥OB,则AE⊥y轴,再由∠BOC=60°得到∠COE=30°,则根据含30度的直角三角形三边的关系得到CE=OE=3,OC=2CE=6,接着根据菱形的性质得OB=OC=6,∠BOA=30°,于是在Rt△BDO中可计算出BD=OB=2,所以D点坐标为(﹣6,2),然后利用反比例函数图象上点的坐标特征可求出k的值.
【解答】解:延长AC交y轴于E,如图,
∵菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,
∴AC∥OB,
∴AE⊥y轴,
∵∠BOC=60°,
∴∠COE=30°,
而顶点C的坐标为(m,3),
∴OE=3,
∴CE=OE=3,
∴OC=2CE=6,
∵四边形ABOC为菱形,
∴OB=OC=6,∠BOA=30°,
在Rt△BDO中,
∵BD=OB=2,
∴D点坐标为(﹣6,2),
∵反比例函数y=的图象经过点D,
∴k=﹣6×2=﹣12.
故答案为﹣12.
15.如图,在四边形ABCD中,DC∥AB,AD=4,DC=5,AB=8.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为每秒1个单位长度.当P点到达C点时,两点同时停止运动,连接PQ.设运动时间为t秒,当△PQB为等腰三角形时,t的值为 、或4 .
【考点】相似三角形的判定与性质;等腰三角形的性质.
【分析】根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
【解答】解:如图1,作CE⊥AB于E,
∵DC∥AB,DA⊥AB,
∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4,
∴BE=3,
∴BC==5,
cos∠B=,
①当PQ=PB时(如图2所示),则BG=BQ,
==,
解得:t=s,
②当PQ=BQ时(如图3所示),则BG=PB,
==,
解得t=s,
③当BP=BQ时(如图4所示),则8﹣t=t,
解得:t=4.
综上所述:当t=s,
s或t=4s时,△PQB为等腰三角形.
故答案为:、或4.
三、解答题(共5小题,满分48分)
16.如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,
AE=CF.
(1)求证:△ABF≌△CDE;
(2)当四边形ABCD满足什么条件时,四边形BFDE是菱形?为什么?
【考点】菱形的判定;全等三角形的判定与性质.
【分析】(1)由平行线的性质得出∠BAC=∠DCA.证出AF=CE.由AAS证明△ABF≌△CDE即可;
(2)先证明四边形ABCD是菱形,得出BD⊥AC,再证明四边形BFDE是平行四边形,即可得出结论.
【解答】(1)证明:∵AB∥CD,
∴∠BAC=∠DCA.
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△ABF和△CDE中,
,
又∵∠ABF=∠CDE,
∴△ABF≌△CDE(AAS);
(2)解:当四边形ABCD满足AB=AD时,四边形BEDF是菱形.理由如下:
连接BD交AC于点O,如图所示:
由(1)得:△ABF≌△CDE,
∴AB=CD,BF=DE,∠AFB=∠CED,
∴BF∥DE.
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴平行四边形ABCD是菱形.
∴BD⊥AC.
∵BF=DE,BF∥DE,
∴四边形BEDF是平行四边形,
∴四边形BEDF是菱形.
17.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
【考点】根的判别式;等腰三角形的判定;勾股定理的逆定理.
【分析】(1)根据方程解的定义把x=﹣1代入方程得到(a+c)×(﹣1)2﹣2b+(a﹣c)=0,整理得a﹣b=0,即a=b,于是根据等腰三角形的判定即可得到△ABC是等腰三角形;
(2)根据判别式的意义得到△=(2b)2﹣4(a+c)(a﹣c)=0,整理得a2=b2+c2,然后根据勾股定理的逆定理得到△ABC是直角三角形.
【解答】解:(1)△ABC是等腰三角形.理由如下:
∵x=﹣1是方程的根,
∴(a+c)×(﹣1)2﹣2b+(a﹣c)=0,
∴a+c﹣2b+a﹣c=0,
∴a﹣b=0,
∴a=b,
∴△ABC是等腰三角形;
(2)△ABC是直角三角形.理由如下:
∵方程有两个相等的实数根,
∴△=(2b)2﹣4(a+c)(a﹣c)=0,
∴4b2﹣4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形.
18.如图,在平面直角坐标系中,一次函数y=ax+b的图象于反比例函数y=的图象相交于点A(﹣4,﹣2),B(m,4),与y轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)观察函数图象,直接写出一次函数图象在反比例函数图象上方时,自变量x的取值范围.
【考点】反比例函数与一次函数的交点问题.
【分析】(1)把A(﹣4,﹣2)代入y=求出看,即可得出反比例函数的表达式,把B(m,4)代入y=求出B的坐标,把A、B的坐标代入y=kx+b得出,求出k、b,即可求出一次函数的表达式;
(2)把x=0代入y=x+2求出OC,分别求出△AOC和△BOC的面积,相加即可;
(3)根据A、B的坐标和图象得出即可.
【解答】解:(1)把A(﹣4,﹣2)代入y=得:k=8,
即反比例函数的表达式为y=,
把B(m,4)代入y=得:4=,
解得:m=2,
即B(2,4),
把A、B的坐标代入y=kx+b得:,
解得:k=1,b=2,
即一次函数的表达式为y=x+2;
(2)把x=0代入y=x+2得:y=2,
即OC=2,
所以△AOB的面积为:×2×|﹣4|+×2×2=6;
(3)由图象可知:一次函数图象在反比例函数图象上方时,自变量x的取值范围是x>2或﹣4<x<0.
19.某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销,购进价格为每件10元,若售价为12元/件,则可全部售出;若每涨价0.1元,销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少m%.结果10月份利润达到3300元,求m的值(m>0).
【考点】一元二次方程的应用;一元一次不等式的应用.
【分析】(1)设售价应为x元,根据不等关系:该文具店在9月份销售量不低于1100件,列出不等式求解即可;
(2)先求出10月份的进价,再根据等量关系:10月份利润达到3300元,列出方程求解即可.
【解答】解:(1)设售价应为x元,依题意有
1160﹣≥1100,
解得:x≤15.
答:售价应不高于15元.
(2)10月份的进价:10(1+20%)=12(元),
由题意得:
1100(1+m%)[15(1﹣m%)﹣12]=3300,
设m%=t,化简得2t2﹣t=0,
解得:t1=0,t2=0.5,
所以m1=0,m2=50%,
因为m>0,
所以m=50.
答:m的值为50.
20.在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.
特殊发现:
如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:
把图1中的△AEF绕着点A顺时针旋转.
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
【考点】几何变换综合题.
【分析】(1)首先过点P作PM⊥CE于点M,然后根据EF⊥AE,BC⊥AC,可得EF∥MP∥CB,推得,再根据点P是BF的中点,可得EM=MC,据此推得PC=PE即可.
(2)首先过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,然后根据全等三角形判定的方法,判断出△DAF≌△EAF,即可判断出AD=AE;再判断出△DAP≌△EAP,即可判断出PD=PE;最后根据FD⊥AC,BC⊥AC,PM⊥AC,可得FD∥BC∥PM,再根据点P是BF的中点,推得PC=PD,再根据PD=PE,即可推得PC=PE.
(3)首先根据△CPE总是等边三角形,可得将△AEF绕着点A顺时针旋转180°,△CPE仍是等边三角形;然后根据∠BCF=∠BEF=90°,点P是BF的中点,可得点C、E在以点P为圆心,BF为直径的圆上;最后根据圆周角定理,求出∠CBE的度数,即可求出当△CPE总是等边三角形时,k的值是多少.
【解答】解:(1)如图2,过点P作PM⊥CE于点M,
,
PC=PE成立,理由如下:
∵EF⊥AE,BC⊥AC,
∴EF∥MP∥CB,
∴,
∵点P是BF的中点,
∴EM=MC,
又∵PM⊥CE,
∴PC=PE.
(2)如图3,过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,
,
PC=PE成立,理由如下:
∵∠DAF=∠EAF,∠FDA=∠FEA=90°,
在△DAF和△EAF中,
,
∴△DAF≌△EAF(AAS),
∴AD=AE,
在△DAP和△EAP中,
,
∴△DAP≌△EAP(SAS),
∴PD=PE,
∵FD⊥AC,BC⊥AC,PM⊥AC,
∴FD∥BC∥PM,
∴,
∵点P是BF的中点,
∴DM=MC,
又∵PM⊥AC,
∴PC=PD,
又∵PD=PE,
∴PC=PE.
(3)如图4,,
∵△CPE总是等边三角形,
∴将△AEF绕着点A顺时针旋转180°,△CPE仍是等边三角形,
∵∠BCF=∠BEF=90°,点P是BF的中点,
∴点C、E在以点P为圆心,BF为直径的圆上,
∵△CPE是等边三角形,
∴∠CPE=60°,
根据圆周角定理,可得
∠CBE=∠CPE=60°=30°,
即∠ABC=30°,
在Rt△ABC中,
∵=k,
=tan30°,
∴k=tan30°=,
∴当k为时,△CPE总是等边三角形.
2017年2月21日
第1页(共28页)
同课章节目录
