第01周 3.1圆--3.4圆周角与圆心角的关系同步测试
文档属性
| 名称 | 第01周 3.1圆--3.4圆周角与圆心角的关系同步测试 |  | |
| 格式 | zip | ||
| 文件大小 | 248.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 21:02:24 | ||
图片预览


文档简介
【北师大版九年级数学(下)周周测】
第 1周测试卷
(测试范围:3.1圆——3.4圆周角与圆心角的关系)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共30分)
1.⊙O的半径为R,点P到圆心O的距离为d,并且d ≥ R,则P点
A.在⊙O内或圆周上 B.在⊙O外
C.在圆周上 D.在⊙O外或圆周上
2.已知OA=5cm,以O为圆心,r为半径作⊙O.若点A在⊙O内,则r的值可以是
A.3cm B.4cm C.5cm D.6cm
3.如图,以点P为圆心,以为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为( )21·cn·jy·com
A.(4,) B.(4,2) C.(4,4) D.(2,)
4.下列说法错误的是( )
A. 面积相等的两个圆是等圆 B. 半径相等的两个半圆是等弧
C. 直径是圆中最长的弦 D. 长度相等的两条弧是等弧
5.如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为( ).2·1·c·n·j·y
A.2m B.2.5m C.4m D.5m
6.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
7.如图,C是⊙O上一点,O是圆心.若∠AOB=80°,则∠ACB的度数为( )
A.80° B.100° C.160° D. 40°
8.如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAC=22°,则∠ADC的度数是( )
A.22° B.58° C.68° D.78°
9.如图,已知⊙O中∠AOB度数为100°,C是圆周上的一点,则∠ACB的度数为( )
A.130° B.100° C.80° D.50°
10.如图D,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )www-2-1-cnjy-com
A. B. C.4 D.3
二、填空题:(每小题3分共30分)
11.圆中最长的弦是 .
12.如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是 .21*cnjy*com
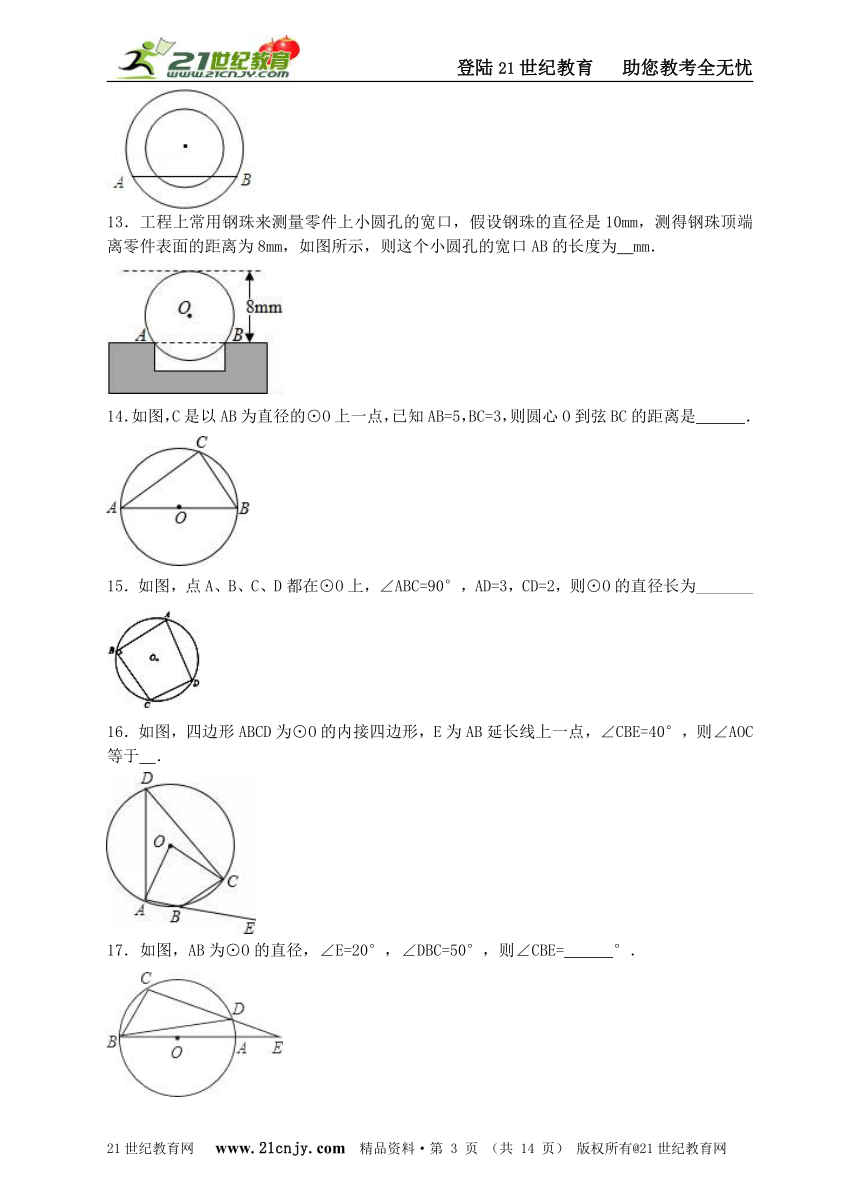
13.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.
14.如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是 .
15.如图,点A、B、C、D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径长为_______
16.如图,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,∠CBE=40°,则∠AOC等于 .21教育名师原创作品
17.如图,AB为⊙O的直径,∠E=20°,∠DBC=50°,则∠CBE= °.
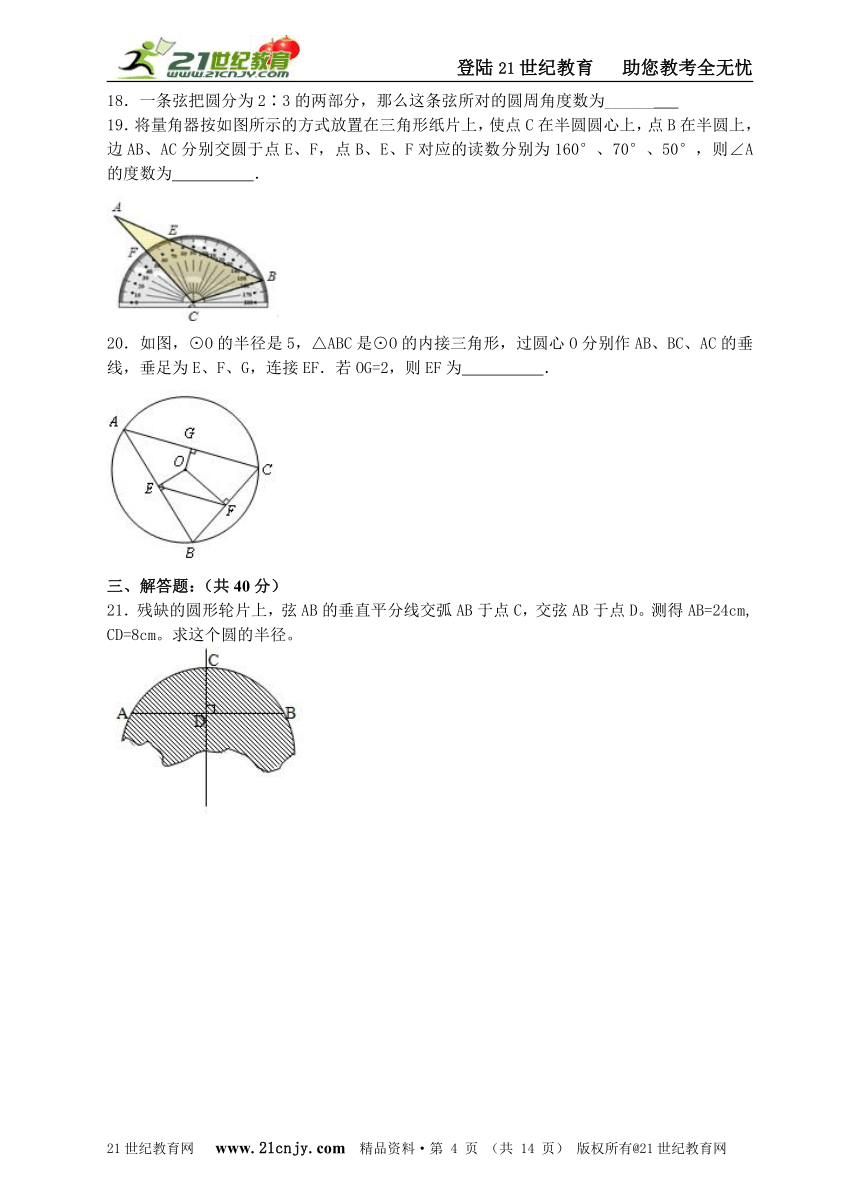
18.一条弦把圆分为2∶3的两部分,那么这条弦所对的圆周角度数为______
19.将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为 .21教育网
20.如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG=2,则EF为 .
三、解答题:(共40分)
21.残缺的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D。测得AB=24cm, CD=8cm。求这个圆的半径。
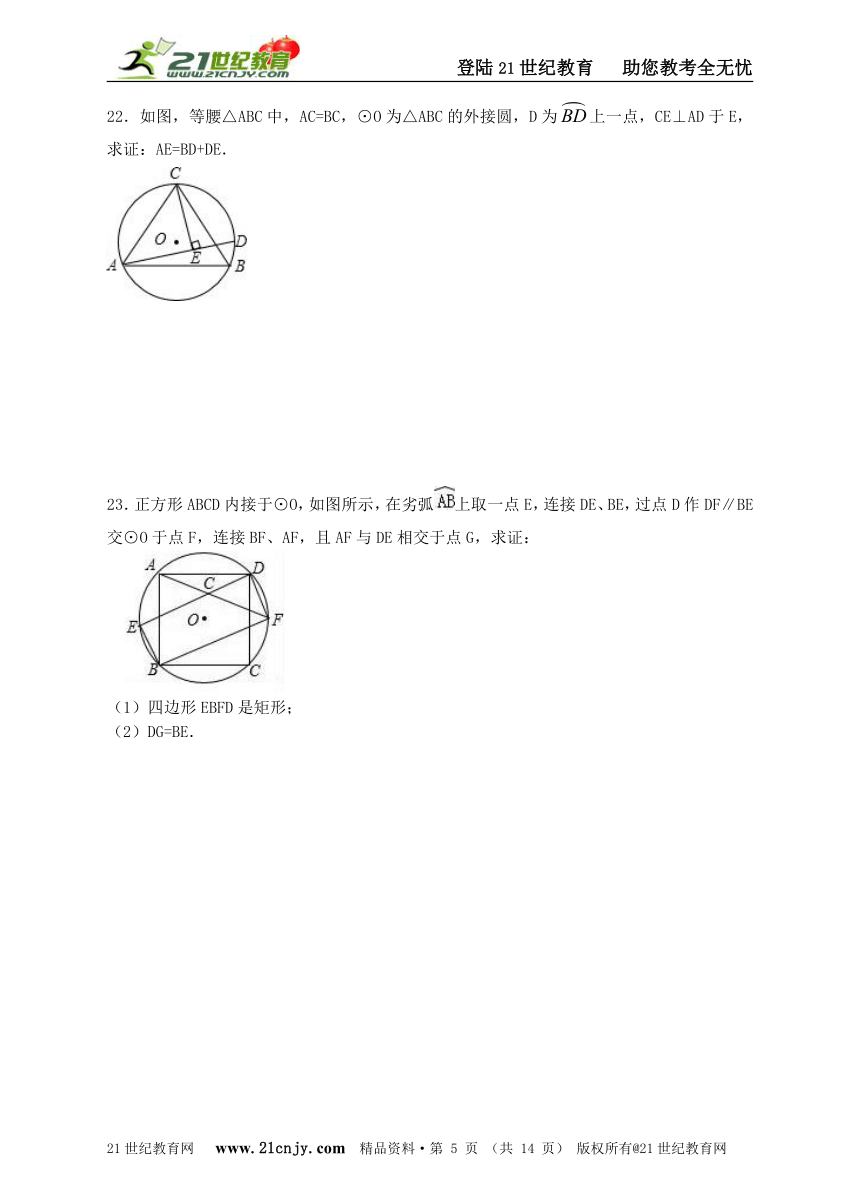
22.如图,等腰△ABC中,AC=BC,⊙O为△ABC的外接圆,D为上一点,CE⊥AD于E,求证:AE=BD+DE.www.21-cn-jy.com
23.正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:【版权所有:21教育】
(1)四边形EBFD是矩形;
(2)DG=BE.
24.如图,BC为⊙O的直径,AD⊥BC,垂足为D,,BF与AD交于E.
(1)求证:AE=BE;
(2)若A,F把半圆三等分,BC=12,求AE的长.
参考答案
1.D
【解析】
试题分析:因为⊙O的半径为R,点P到圆心O的距离为d,所以当d>R时, P点在⊙O外,当d=R时, P点在圆周上,所以d ≥ R,时P点在⊙O外或圆周上,故选:D.
2.D
【解析】
试题分析:因为OA=5cm,所以当d= OA=5<r时,点A在⊙O内,所以选:D.
3.C.
【解析】
试题分析:过点P作PC⊥AB于点C;
即点C为AB的中点,又点A的坐标为(2,0),点B的坐标为(6,0),故点C(4,0)
在Rt△PAC中,PA=,AC=2,即有PC=4,即P(4,4).
故选C.
4.D
【解析】
试题分析:等弧是指弧的长度和度数都相等的两条弧.
5.B.
【解析】
试题分析:先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD=AB=×4=2m,设OA=r,则OD=r﹣1,在Rt△AOD中,由勾股定理得,即,解得r=2.5m.【来源:21cnj*y.co*m】
故选:B.
6.C.
【解析】
试题分析:由BD是⊙O的直径,根据直径所对的圆周角是直角,得∠BCD=90°,可求∠D=60°,即可求∠A=∠D=60°.故选C.21·世纪*教育网
7.D
【解析】
试题分析:同弧所对的圆心角的度数等于圆周角度数的2倍.
8.C.
【解析】
试题分析:根据直径所对的圆周角是直角求得∠ACB=90°,则根据直角三角形的性质求得∠ABC=90°﹣∠BAC=90°﹣22°=68°,然后根据同弧所对的圆周角相等可得∠ADC=∠ABC=68°.故选C.21*cnjy*com
9.A.
【解析】
试题分析:在优弧AB上取点D,连接AD,BD,∵∠D=∠AOB=×100°=50°,∴∠ACB=180°﹣∠D=130°.故选A.
10.D
【解析】
试题分析:作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,再证明△ADE≌△ABF,得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=BF=3.
故选:D.
11.直径
【解析】
试题分析:根据圆的性质直接回答即可.
解:圆中最长的弦是直径,
故答案为:直径.
12.8<AB≤10.
【解析】
试题分析:如图,当AB与小圆相切时有一个公共点D,连接OA,OD,可得OD⊥AB,∴D为AB的中点,即AD=BD,在Rt△ADO中,OD=3,OA=5,∴AD=4,∴AB=2AD=8;
当AB经过同心圆的圆心时,弦AB最大且与小圆相交有两个公共点,此时AB=10,所以AB的取值范围是8<AB≤10.故答案为:8<AB≤10.
13.8
【解析】
试题分析:先求出钢珠的半径及OD=3mm,连接OA,过点O作OD⊥AB于点D,则AB=2AD,在Rt△AOD中利用勾股定理即可求出AD4mm,进而得出AB=8mm.2-1-c-n-j-y
14.2.
【解析】
试题分析:过O点作OD⊥BC,D点为垂足,则DB=DC,所以OD为△BAC的中位线,即有OD=AC;由AB为⊙O的直径,得到∠ACB=90°,由勾股定理可求得AC,即可得到OD的长.
解:过O点作OD⊥BC,D点为垂足,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AB2=BC2+AC2,即AC==4,
又∵OD⊥BC,
∴DB=DC,而OA=OB,
∴OD为△BAC的中位线,即有OD=AC,
所以OD=×4=2,即圆心O到弦BC的距离为2.
故答案为2.
15.
【解析】
试题分析:连接AC,根据∠ABC=90°可得AC为直径,则∠ADC=90°,根据Rt△ACD的勾股定理可得:AC=.【出处:21教育名师】
16.80°
【解析】
试题分析:先根据补角的性质求出∠ABC180°﹣∠CBE=180°﹣40°=140°,再由圆内接四边形的性质求出∠ADC=180°﹣∠ABC=180°﹣140°=40°,由圆周角定理即可得出∠AOC=2∠D=2×40°=80°.
17.60°.
【解析】
试题解析:连接AC,
∵∠DBA和∠DCA都为所对的圆周角,
∴∠DBA=∠DCA,
∵AB为⊙O的直径,
∴∠BCA=90°,
∴∠CBA+∠CAB=90°,
∵∠CAB=∠E+∠DCA,
∴∠CBD+∠DBA+∠E+∠DBA=90°,
∵∠E=20°,∠DBC=50°,
∴∠DBA=10°,
∴∠CBE=∠DBA+∠CBD=10°+50°=60°.
18.72°或108°.
【解析】
试题解析:如图,连接OA、OB.
弦AB将⊙O分为2:3两部分,
则∠AOB=×360°=144°;
∴∠ACB=∠AOB=72°,
∠ADB=180°-∠ACB=108°;
故这条弦所对的圆周角的度数为72°或108°.
19.25 o .
【解析】
试题分析:设量角器的半圆直径为MN,因为点B、E、F对应的读数分别为160°、70°、50°,所以∠BOM=160°,∠EOM=70°,∠FOM=50°,所以∠BOE=160°-70°=90o,所以∠CEB=∠B=45o,所以∠EOF=70°-50°=20o,根据三角形的外角性质得:∠A=∠CEB-∠EOF=45o-20o=25 o .
20..
【解析】
试题分析:连结OA,根据垂径定理由OG⊥AC得到AG=CG,在Rt△AOG中,根据勾股定理得AG=,则AC=2AG=2,再根据垂径定理由OE⊥AB,OF⊥BC得到AE=BE,CF=BF,所以EF为△ABC的中位线,则EF=AC=.
试题解析:连结OA,如图,
∵OG⊥AC,
∴AG=CG,
在Rt△AOG中,OG=2,OA=5,
∴AG=,
∴AC=2AG=2,
∵OE⊥AB,OF⊥BC,
∴AE=BE,CF=BF,
∴EF为△ABC的中位线,
∴EF=AC=.
21.13
【解析】
试题分析:设这个圆的圆心是O,连接OA,设OA=x,则AD=12cm,CD=(x-8)cm,根据勾股定理得出x的值,从而得出答案.【来源:21·世纪·教育·网】
试题解析:设这个圆的圆心是O , 连接OA,设OA=x,AD=12cm,OD=(x-8)cm,
则根据勾股定理列方程:x2=122+(x-8)2, 解得:x=13.
答:圆的半径为13cm.
22.证明详见解析.
【解析】
试题分析:如图,在AE上截取AF=BD,连接CF,由圆周角定理得,∠CBD=∠CAF,根据SAS可以利用已知条件证明△ACF≌△BCD?CF=CD,由于CE⊥AD,根据等腰三角形的性质:底边上的高与底边上的中线重合知,EF=DE,则AE=AF+EF=BD+DE.21世纪教育网版权所有
试题解析:证明:如图,在AE上截取AF=BD,连接CF,CD;在△ACF和△BCD中,
,
∴△ACF≌△BCD,
∴CF=CD,
∵CE⊥AD于E,
∴EF=DE,
∴AE=AF+EF=BD+DE.
23.(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)根据正方形的性质、圆周角定理及平行线的性质易证∠BED=∠BAD=90°,∠BFD=∠BCD=90°,∠EDF=90°,即可判定四边形EBFD是矩形;(2)根据正方形的性质可得的度数是90°,进而得出BE=DF,则BE=DG.21cnjy.com
试题解析:(1)∵正方形ABCD内接于⊙O,
∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,
又∵DF∥BE,
∴∠EDF+∠BED=180°,
∴∠EDF=90°,
∴四边形EBFD是矩形;
(2))∵正方形ABCD内接于⊙O,
∴的度数是90°,
∴∠AFD=45°,
又∵∠GDF=90°,
∴∠DGF=∠DFC=45°,
∴DG=DF,
又∵在矩形EBFD中,BE=DF,
∴BE=DG.
24.(1)证明详见解析;(2) .
【解析】
试题分析:(1)连AC,要证明AE=BE,只要证∠ABE=∠BAE;BC为⊙O的直径,得到∠BAC=90°,而AD⊥BC,可得∠BAD=∠ACB,由,得∠ACB=∠ABF,这样就有∠ABE=∠BAE;
(2)由A,F把半圆三等分,得到∠ACB=∠CBF=30°,而BC=12,得到AB=6,再根据∠BAD=∠ACB,得到∠BAD=30°,所以BD=3,最后在Rt△BDE中,∠CBF=30°,BD=3,即可求出BE.
试题解析:(1)连AC,如图,
∵BC为⊙O的直径,
∴∠BAC=90°,
又∵AD⊥BC,
∴∠BAD=∠ACB,
又∵,
∴∠ACB=∠ABF,
∴∠ABE=∠BAE,
∴AE=BE;
(2)∵A,F把半圆三等分,
∴∠ACB=∠CBF=∠ABF=30°,
∴∠BAD=30°,
在Rt△ABC中,BC=12,所以AB=BC=6,
在Rt△ABD中,AB=6,所以BD=AB=3,
Rt△BDE中,∠CBF=30°,BD=3,
∴DE==,
∴BE=,
所以AE=.
第 1周测试卷
(测试范围:3.1圆——3.4圆周角与圆心角的关系)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共30分)
1.⊙O的半径为R,点P到圆心O的距离为d,并且d ≥ R,则P点
A.在⊙O内或圆周上 B.在⊙O外
C.在圆周上 D.在⊙O外或圆周上
2.已知OA=5cm,以O为圆心,r为半径作⊙O.若点A在⊙O内,则r的值可以是
A.3cm B.4cm C.5cm D.6cm
3.如图,以点P为圆心,以为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为( )21·cn·jy·com
A.(4,) B.(4,2) C.(4,4) D.(2,)
4.下列说法错误的是( )
A. 面积相等的两个圆是等圆 B. 半径相等的两个半圆是等弧
C. 直径是圆中最长的弦 D. 长度相等的两条弧是等弧
5.如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为( ).2·1·c·n·j·y
A.2m B.2.5m C.4m D.5m
6.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
7.如图,C是⊙O上一点,O是圆心.若∠AOB=80°,则∠ACB的度数为( )
A.80° B.100° C.160° D. 40°
8.如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAC=22°,则∠ADC的度数是( )
A.22° B.58° C.68° D.78°
9.如图,已知⊙O中∠AOB度数为100°,C是圆周上的一点,则∠ACB的度数为( )
A.130° B.100° C.80° D.50°
10.如图D,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )www-2-1-cnjy-com
A. B. C.4 D.3
二、填空题:(每小题3分共30分)
11.圆中最长的弦是 .
12.如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是 .21*cnjy*com
13.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.
14.如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是 .
15.如图,点A、B、C、D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径长为_______
16.如图,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,∠CBE=40°,则∠AOC等于 .21教育名师原创作品
17.如图,AB为⊙O的直径,∠E=20°,∠DBC=50°,则∠CBE= °.
18.一条弦把圆分为2∶3的两部分,那么这条弦所对的圆周角度数为______
19.将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为 .21教育网
20.如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG=2,则EF为 .
三、解答题:(共40分)
21.残缺的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D。测得AB=24cm, CD=8cm。求这个圆的半径。
22.如图,等腰△ABC中,AC=BC,⊙O为△ABC的外接圆,D为上一点,CE⊥AD于E,求证:AE=BD+DE.www.21-cn-jy.com
23.正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:【版权所有:21教育】
(1)四边形EBFD是矩形;
(2)DG=BE.
24.如图,BC为⊙O的直径,AD⊥BC,垂足为D,,BF与AD交于E.
(1)求证:AE=BE;
(2)若A,F把半圆三等分,BC=12,求AE的长.
参考答案
1.D
【解析】
试题分析:因为⊙O的半径为R,点P到圆心O的距离为d,所以当d>R时, P点在⊙O外,当d=R时, P点在圆周上,所以d ≥ R,时P点在⊙O外或圆周上,故选:D.
2.D
【解析】
试题分析:因为OA=5cm,所以当d= OA=5<r时,点A在⊙O内,所以选:D.
3.C.
【解析】
试题分析:过点P作PC⊥AB于点C;
即点C为AB的中点,又点A的坐标为(2,0),点B的坐标为(6,0),故点C(4,0)
在Rt△PAC中,PA=,AC=2,即有PC=4,即P(4,4).
故选C.
4.D
【解析】
试题分析:等弧是指弧的长度和度数都相等的两条弧.
5.B.
【解析】
试题分析:先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD=AB=×4=2m,设OA=r,则OD=r﹣1,在Rt△AOD中,由勾股定理得,即,解得r=2.5m.【来源:21cnj*y.co*m】
故选:B.
6.C.
【解析】
试题分析:由BD是⊙O的直径,根据直径所对的圆周角是直角,得∠BCD=90°,可求∠D=60°,即可求∠A=∠D=60°.故选C.21·世纪*教育网
7.D
【解析】
试题分析:同弧所对的圆心角的度数等于圆周角度数的2倍.
8.C.
【解析】
试题分析:根据直径所对的圆周角是直角求得∠ACB=90°,则根据直角三角形的性质求得∠ABC=90°﹣∠BAC=90°﹣22°=68°,然后根据同弧所对的圆周角相等可得∠ADC=∠ABC=68°.故选C.21*cnjy*com
9.A.
【解析】
试题分析:在优弧AB上取点D,连接AD,BD,∵∠D=∠AOB=×100°=50°,∴∠ACB=180°﹣∠D=130°.故选A.
10.D
【解析】
试题分析:作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,再证明△ADE≌△ABF,得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=BF=3.
故选:D.
11.直径
【解析】
试题分析:根据圆的性质直接回答即可.
解:圆中最长的弦是直径,
故答案为:直径.
12.8<AB≤10.
【解析】
试题分析:如图,当AB与小圆相切时有一个公共点D,连接OA,OD,可得OD⊥AB,∴D为AB的中点,即AD=BD,在Rt△ADO中,OD=3,OA=5,∴AD=4,∴AB=2AD=8;
当AB经过同心圆的圆心时,弦AB最大且与小圆相交有两个公共点,此时AB=10,所以AB的取值范围是8<AB≤10.故答案为:8<AB≤10.
13.8
【解析】
试题分析:先求出钢珠的半径及OD=3mm,连接OA,过点O作OD⊥AB于点D,则AB=2AD,在Rt△AOD中利用勾股定理即可求出AD4mm,进而得出AB=8mm.2-1-c-n-j-y
14.2.
【解析】
试题分析:过O点作OD⊥BC,D点为垂足,则DB=DC,所以OD为△BAC的中位线,即有OD=AC;由AB为⊙O的直径,得到∠ACB=90°,由勾股定理可求得AC,即可得到OD的长.
解:过O点作OD⊥BC,D点为垂足,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AB2=BC2+AC2,即AC==4,
又∵OD⊥BC,
∴DB=DC,而OA=OB,
∴OD为△BAC的中位线,即有OD=AC,
所以OD=×4=2,即圆心O到弦BC的距离为2.
故答案为2.
15.
【解析】
试题分析:连接AC,根据∠ABC=90°可得AC为直径,则∠ADC=90°,根据Rt△ACD的勾股定理可得:AC=.【出处:21教育名师】
16.80°
【解析】
试题分析:先根据补角的性质求出∠ABC180°﹣∠CBE=180°﹣40°=140°,再由圆内接四边形的性质求出∠ADC=180°﹣∠ABC=180°﹣140°=40°,由圆周角定理即可得出∠AOC=2∠D=2×40°=80°.
17.60°.
【解析】
试题解析:连接AC,
∵∠DBA和∠DCA都为所对的圆周角,
∴∠DBA=∠DCA,
∵AB为⊙O的直径,
∴∠BCA=90°,
∴∠CBA+∠CAB=90°,
∵∠CAB=∠E+∠DCA,
∴∠CBD+∠DBA+∠E+∠DBA=90°,
∵∠E=20°,∠DBC=50°,
∴∠DBA=10°,
∴∠CBE=∠DBA+∠CBD=10°+50°=60°.
18.72°或108°.
【解析】
试题解析:如图,连接OA、OB.
弦AB将⊙O分为2:3两部分,
则∠AOB=×360°=144°;
∴∠ACB=∠AOB=72°,
∠ADB=180°-∠ACB=108°;
故这条弦所对的圆周角的度数为72°或108°.
19.25 o .
【解析】
试题分析:设量角器的半圆直径为MN,因为点B、E、F对应的读数分别为160°、70°、50°,所以∠BOM=160°,∠EOM=70°,∠FOM=50°,所以∠BOE=160°-70°=90o,所以∠CEB=∠B=45o,所以∠EOF=70°-50°=20o,根据三角形的外角性质得:∠A=∠CEB-∠EOF=45o-20o=25 o .
20..
【解析】
试题分析:连结OA,根据垂径定理由OG⊥AC得到AG=CG,在Rt△AOG中,根据勾股定理得AG=,则AC=2AG=2,再根据垂径定理由OE⊥AB,OF⊥BC得到AE=BE,CF=BF,所以EF为△ABC的中位线,则EF=AC=.
试题解析:连结OA,如图,
∵OG⊥AC,
∴AG=CG,
在Rt△AOG中,OG=2,OA=5,
∴AG=,
∴AC=2AG=2,
∵OE⊥AB,OF⊥BC,
∴AE=BE,CF=BF,
∴EF为△ABC的中位线,
∴EF=AC=.
21.13
【解析】
试题分析:设这个圆的圆心是O,连接OA,设OA=x,则AD=12cm,CD=(x-8)cm,根据勾股定理得出x的值,从而得出答案.【来源:21·世纪·教育·网】
试题解析:设这个圆的圆心是O , 连接OA,设OA=x,AD=12cm,OD=(x-8)cm,
则根据勾股定理列方程:x2=122+(x-8)2, 解得:x=13.
答:圆的半径为13cm.
22.证明详见解析.
【解析】
试题分析:如图,在AE上截取AF=BD,连接CF,由圆周角定理得,∠CBD=∠CAF,根据SAS可以利用已知条件证明△ACF≌△BCD?CF=CD,由于CE⊥AD,根据等腰三角形的性质:底边上的高与底边上的中线重合知,EF=DE,则AE=AF+EF=BD+DE.21世纪教育网版权所有
试题解析:证明:如图,在AE上截取AF=BD,连接CF,CD;在△ACF和△BCD中,
,
∴△ACF≌△BCD,
∴CF=CD,
∵CE⊥AD于E,
∴EF=DE,
∴AE=AF+EF=BD+DE.
23.(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)根据正方形的性质、圆周角定理及平行线的性质易证∠BED=∠BAD=90°,∠BFD=∠BCD=90°,∠EDF=90°,即可判定四边形EBFD是矩形;(2)根据正方形的性质可得的度数是90°,进而得出BE=DF,则BE=DG.21cnjy.com
试题解析:(1)∵正方形ABCD内接于⊙O,
∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,
又∵DF∥BE,
∴∠EDF+∠BED=180°,
∴∠EDF=90°,
∴四边形EBFD是矩形;
(2))∵正方形ABCD内接于⊙O,
∴的度数是90°,
∴∠AFD=45°,
又∵∠GDF=90°,
∴∠DGF=∠DFC=45°,
∴DG=DF,
又∵在矩形EBFD中,BE=DF,
∴BE=DG.
24.(1)证明详见解析;(2) .
【解析】
试题分析:(1)连AC,要证明AE=BE,只要证∠ABE=∠BAE;BC为⊙O的直径,得到∠BAC=90°,而AD⊥BC,可得∠BAD=∠ACB,由,得∠ACB=∠ABF,这样就有∠ABE=∠BAE;
(2)由A,F把半圆三等分,得到∠ACB=∠CBF=30°,而BC=12,得到AB=6,再根据∠BAD=∠ACB,得到∠BAD=30°,所以BD=3,最后在Rt△BDE中,∠CBF=30°,BD=3,即可求出BE.
试题解析:(1)连AC,如图,
∵BC为⊙O的直径,
∴∠BAC=90°,
又∵AD⊥BC,
∴∠BAD=∠ACB,
又∵,
∴∠ACB=∠ABF,
∴∠ABE=∠BAE,
∴AE=BE;
(2)∵A,F把半圆三等分,
∴∠ACB=∠CBF=∠ABF=30°,
∴∠BAD=30°,
在Rt△ABC中,BC=12,所以AB=BC=6,
在Rt△ABD中,AB=6,所以BD=AB=3,
Rt△BDE中,∠CBF=30°,BD=3,
∴DE==,
∴BE=,
所以AE=.
