1.1.1 正切课件
图片预览






文档简介
课件29张PPT。第一章 直角三角形的边角关系1.1 锐角三角函数第1课时 正 切1课堂讲解正切的定义
正切的应用
坡度和坡角2课时流程逐点
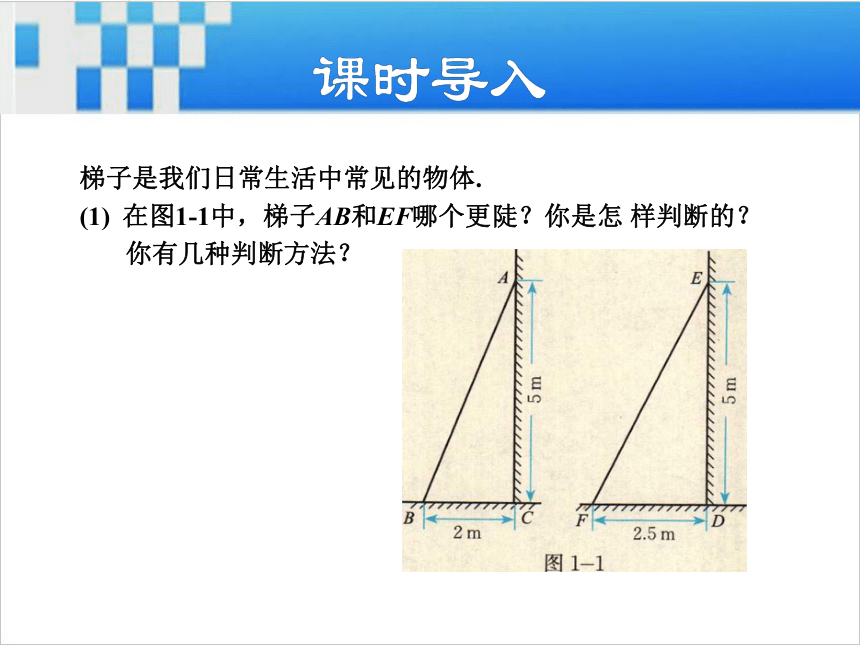
导讲练课堂小结作业提升梯子是我们日常生活中常见的物体.
在图1-1中,梯子AB和EF哪个更陡?你是怎 样判断的?
你有几种判断方法?
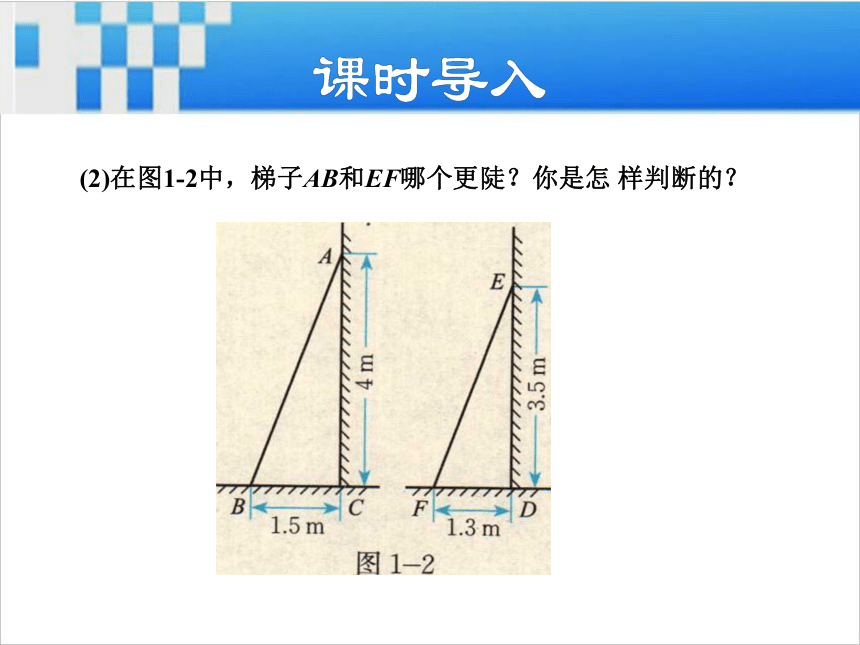
(2)在图1-2中,梯子AB和EF哪个更陡?你是怎 样判断的?
1知识点正切的定义想一想
如图1-3,小明想通过测量
B1C1及AC1,算出它们的比,
来说明梯子的倾斜程度;而
小亮则认为,通过测量B2C2
及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?知1-导(1) 直角三角形AB1C1和直角三角形AB2C2有什么关系?
有什么关系?
如果改变B2在梯子上的位置呢?由此你能得出什么
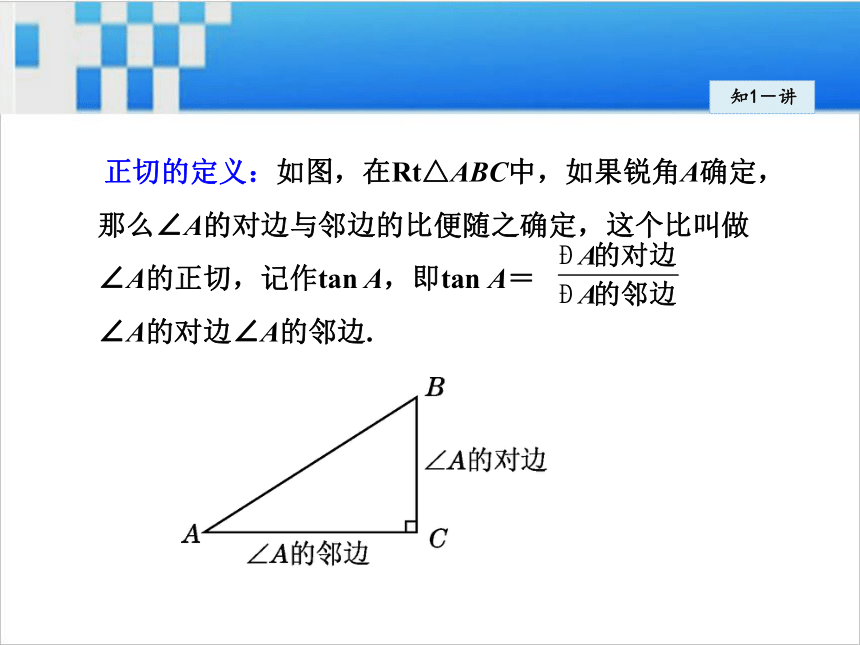
结论?知1-导知1-导改变点B的位置, 的值始终不变。 正切的定义:如图,在Rt△ABC中,如果锐角A确定,
那么∠A的对边与邻边的比便随之确定,这个比叫做
∠A的正切,记作tan A,即tan A=
∠A的对边∠A的邻边.知1-讲要点精析:
(1)tan A表示锐角A的正切,一般省略“∠”,但当用三
个字母表示角时,不能省略“∠”.如tan ∠ABC.
(2)∠A的范围与tan A的范围:①0°<∠A<90°;
②tan A>0.
(3)tan A随着∠A的增大而增大,∠A越接近90°,tan A
的值就增加得越快,tan A可以等于任何一个正数.
(4)正切值的大小由锐角的度数决定,与其在哪个直角三
角形中无关.知1-讲例1 如图,在Rt△ABC中,∠C=90°,
则tan A=________.知1-讲由正切定义可知tan A= 在本题中已知两边之比,可运
用参数法,由 可设BC=15a,AB=17a,从而可
用勾股定理表示出第三边AC=8a,再用正切的定义求解得
tan A=导引:知1-讲直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利
用勾股定理求出未知的直角边,再利用正切的定义
求解.例2〈桂林〉如图,在Rt△ABC中,∠ACB=90°,AC=
8,BC=6,CD⊥AB,垂足为D,则tan∠BCD=
________.知1-讲根据题意得∠BCD=∠CAB,
所以tan ∠BCD=tan ∠CAB=导引:知1-讲 直接求某个锐角的正切值有困难时,可以考虑利
用中间量进行转化,可以是相等的角作为中间量,还
可以利用相似,得到相等的比作为中间量.在△ABC中,AC=5,BC=4,AB=3,那么下列
各式正确的是( )
A.tan A= B.tan A=
C.tan B= D.tan B=知1-练知1-练(2015·包头)在Rt△ABC中,∠C=90°,若斜边AB
是直角边BC的3倍,则tan B的值是( )
A. B.3 C. D.
一个直角三角形中,如果各边的长度都扩大为原来
的2倍,那么它的两个锐角的正切值( )
A.都没有变化
B.都扩大为原来的2倍
C.都缩小为原来的一半
D.不能确定是否发生变化2知识点正切的应用知2-讲议一议
在图1 -3中,梯子的倾斜程度与tanA有关系吗?知2-讲tanA的值越大,梯子越陡.知2-讲1. 当梯子与地面所成的角为锐角A时,
tan A= tan A的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2. 当倾斜角确定时,其对边与邻边之比随之确定,这一比
值只与倾斜角的大小有关,而与物体的长度无关.
知2-讲例3 如图表示甲、乙两个自动扶梯,哪一个自动扶梯比 较陡?
解:甲梯中,
乙梯中,
因为tanα>tanβ,所以甲梯更陡.知2-讲(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾
斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程
度,因为夹角的正切值越大,则夹角越大,物体放
置得越“陡”.(2016·安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2
B.
C.
D.
知2-练知2-练如图,P是α的边OA上一点,且点P的坐标为(3,4),
则tan α的值为( )
A. B.
C. D.
在Rt△ABC中,CD为斜边AB上的高,且CD=2,
BD=8,则tan A的值是( )
A.2 B.4 C. D.知2-练4 (2015·荆门)如图,在△ABC中,∠BAC=90°,
AB=AC,点D 为边AC的中点,DE⊥BC于点E,
连接BD,则tan ∠DBC的值为( )
A. B.
C. D.
知3-讲3知识点坡度和坡角1.定义:如图,坡面的铅直高度h与水平宽度l的比称
为坡度(或坡比),一般用i表示.
2.表示方法:把坡面与水平
面的夹角称为坡角,坡
度是坡角的正切值,
即i=tan α= .例4 以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
错解分析:概念不清,误以为坡度是一个角度,而猜测
坡度即为倾斜角的度数.
知3-讲B知3-讲 坡度的概念,一要记住是一个比值而不是角度,
二要明确坡度其实就是坡角的正切.(中考·怀化)如图,小明爬一土坡,他从A处爬到B处
所走的直线距离AB=4 m,此时,他离地面的高度
为h=2 m,则这个土坡的坡角∠A=________.知3-练如图,铁路路基横断面为一个四边形,其中AD∥BC.
若两斜坡的坡度均为i=2∶3,顶宽是3 m,路基高是
4 m,则路基的下底宽是( )
A.7 m B.9 m C.12 m D.15 m知3-练这节课我的收获是什么?有什么经验与同学们分享?
正切的应用
坡度和坡角2课时流程逐点
导讲练课堂小结作业提升梯子是我们日常生活中常见的物体.
在图1-1中,梯子AB和EF哪个更陡?你是怎 样判断的?
你有几种判断方法?
(2)在图1-2中,梯子AB和EF哪个更陡?你是怎 样判断的?
1知识点正切的定义想一想
如图1-3,小明想通过测量
B1C1及AC1,算出它们的比,
来说明梯子的倾斜程度;而
小亮则认为,通过测量B2C2
及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?知1-导(1) 直角三角形AB1C1和直角三角形AB2C2有什么关系?
有什么关系?
如果改变B2在梯子上的位置呢?由此你能得出什么
结论?知1-导知1-导改变点B的位置, 的值始终不变。 正切的定义:如图,在Rt△ABC中,如果锐角A确定,
那么∠A的对边与邻边的比便随之确定,这个比叫做
∠A的正切,记作tan A,即tan A=
∠A的对边∠A的邻边.知1-讲要点精析:
(1)tan A表示锐角A的正切,一般省略“∠”,但当用三
个字母表示角时,不能省略“∠”.如tan ∠ABC.
(2)∠A的范围与tan A的范围:①0°<∠A<90°;
②tan A>0.
(3)tan A随着∠A的增大而增大,∠A越接近90°,tan A
的值就增加得越快,tan A可以等于任何一个正数.
(4)正切值的大小由锐角的度数决定,与其在哪个直角三
角形中无关.知1-讲例1 如图,在Rt△ABC中,∠C=90°,
则tan A=________.知1-讲由正切定义可知tan A= 在本题中已知两边之比,可运
用参数法,由 可设BC=15a,AB=17a,从而可
用勾股定理表示出第三边AC=8a,再用正切的定义求解得
tan A=导引:知1-讲直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利
用勾股定理求出未知的直角边,再利用正切的定义
求解.例2〈桂林〉如图,在Rt△ABC中,∠ACB=90°,AC=
8,BC=6,CD⊥AB,垂足为D,则tan∠BCD=
________.知1-讲根据题意得∠BCD=∠CAB,
所以tan ∠BCD=tan ∠CAB=导引:知1-讲 直接求某个锐角的正切值有困难时,可以考虑利
用中间量进行转化,可以是相等的角作为中间量,还
可以利用相似,得到相等的比作为中间量.在△ABC中,AC=5,BC=4,AB=3,那么下列
各式正确的是( )
A.tan A= B.tan A=
C.tan B= D.tan B=知1-练知1-练(2015·包头)在Rt△ABC中,∠C=90°,若斜边AB
是直角边BC的3倍,则tan B的值是( )
A. B.3 C. D.
一个直角三角形中,如果各边的长度都扩大为原来
的2倍,那么它的两个锐角的正切值( )
A.都没有变化
B.都扩大为原来的2倍
C.都缩小为原来的一半
D.不能确定是否发生变化2知识点正切的应用知2-讲议一议
在图1 -3中,梯子的倾斜程度与tanA有关系吗?知2-讲tanA的值越大,梯子越陡.知2-讲1. 当梯子与地面所成的角为锐角A时,
tan A= tan A的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2. 当倾斜角确定时,其对边与邻边之比随之确定,这一比
值只与倾斜角的大小有关,而与物体的长度无关.
知2-讲例3 如图表示甲、乙两个自动扶梯,哪一个自动扶梯比 较陡?
解:甲梯中,
乙梯中,
因为tanα>tanβ,所以甲梯更陡.知2-讲(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾
斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程
度,因为夹角的正切值越大,则夹角越大,物体放
置得越“陡”.(2016·安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2
B.
C.
D.
知2-练知2-练如图,P是α的边OA上一点,且点P的坐标为(3,4),
则tan α的值为( )
A. B.
C. D.
在Rt△ABC中,CD为斜边AB上的高,且CD=2,
BD=8,则tan A的值是( )
A.2 B.4 C. D.知2-练4 (2015·荆门)如图,在△ABC中,∠BAC=90°,
AB=AC,点D 为边AC的中点,DE⊥BC于点E,
连接BD,则tan ∠DBC的值为( )
A. B.
C. D.
知3-讲3知识点坡度和坡角1.定义:如图,坡面的铅直高度h与水平宽度l的比称
为坡度(或坡比),一般用i表示.
2.表示方法:把坡面与水平
面的夹角称为坡角,坡
度是坡角的正切值,
即i=tan α= .例4 以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
错解分析:概念不清,误以为坡度是一个角度,而猜测
坡度即为倾斜角的度数.
知3-讲B知3-讲 坡度的概念,一要记住是一个比值而不是角度,
二要明确坡度其实就是坡角的正切.(中考·怀化)如图,小明爬一土坡,他从A处爬到B处
所走的直线距离AB=4 m,此时,他离地面的高度
为h=2 m,则这个土坡的坡角∠A=________.知3-练如图,铁路路基横断面为一个四边形,其中AD∥BC.
若两斜坡的坡度均为i=2∶3,顶宽是3 m,路基高是
4 m,则路基的下底宽是( )
A.7 m B.9 m C.12 m D.15 m知3-练这节课我的收获是什么?有什么经验与同学们分享?
