2.1 二次函数课件
图片预览








文档简介
课件25张PPT。第二章 二次函数第1节 二次函数1课堂讲解二次函数的定义
利用二次函数的表达式表示实际问题2课时流程逐点
导讲练课堂小结作业提升 某果园有100棵橙子树,平均每棵树结
600个橙子.现准备多种一些橙子树以提高果
园产量,但是如果多种树,那么树之间的距
离和每一棵树所接受的阳光就会减少.根据
经验估计,每多种一棵树,平均每棵树就会
少结5个橙子.
(1)问题中有哪些变量?其中哪些是自变量?哪些是因变量?
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式. 果园共有(100+x)棵树,平均每棵树结(600-5x)
个橙子,因此果园橙子的总产量
y=(600-5x)(100+x)=-5x2+100x+60 000.1知识点二次函数的定义做一做 银行的储蓄利率是随时间变化的,也
就是说,利率是一个变量.在我国,利率的
调整是由中国人民银行根据国民经济发展
的情况而决定的.
设人民币一年定期储蓄的年利率是x,
一年到期后,银行将本金和利息自动按一
年定期储蓄转存.如果存款额是100元,那
么请你写出两年后的本息和y(元)的表达式.知1-导知1-导 (1)两数和是20,设其中一个数是x,你能写出中两
数之积y的表达式吗?
(2)已知矩形的周长为40cm,它的面积可能是100cm2
吗?可能是75cm2吗?还可能是多少?你能表示这个矩形的
面积与其一边长的关系吗?想一想1.定义:一般地,若两个变量x,y之间的对应关系可以表示
成y=ax2+bx+c(a,b,c是常数,a≠0)的形式,则称y是x
的二次函数;其中a是二次项系数,b为一次项系数,c为
常数项.
要点精析:(1)二次函数必须满足三个条件:
①函数表达式为整式;
②函数表达式有唯一的自变量;
③自变量的最高次数是2且二次项系数不等于0.
(2)二次函数中自变量的取值范围是一切实数,函数值范围不
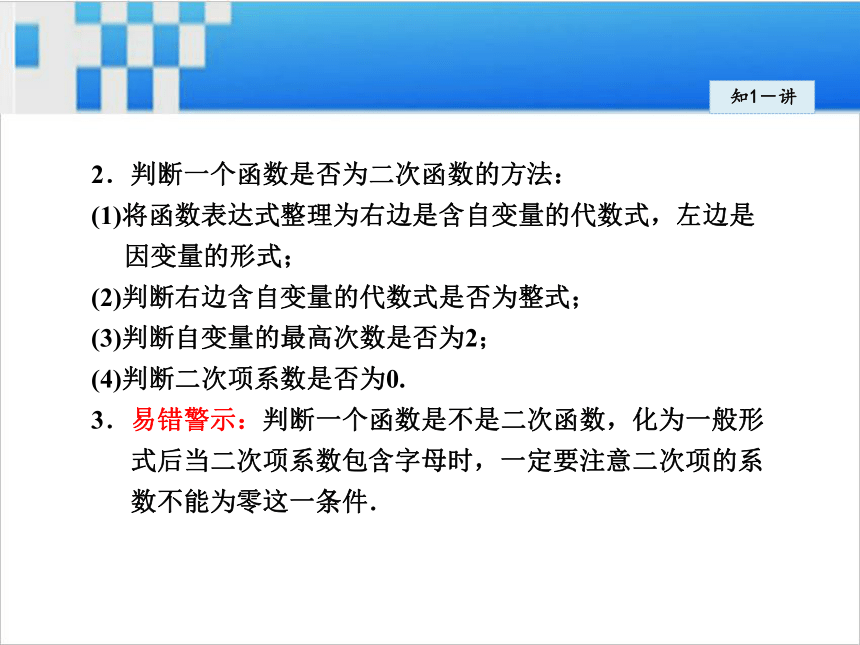
是一切实数.知1-讲2.判断一个函数是否为二次函数的方法:
(1)将函数表达式整理为右边是含自变量的代数式,左边是
因变量的形式;
(2)判断右边含自变量的代数式是否为整式;
(3)判断自变量的最高次数是否为2;
(4)判断二次项系数是否为0.
3.易错警示:判断一个函数是不是二次函数,化为一般形
式后当二次项系数包含字母时,一定要注意二次项的系
数不能为零这一条件.知1-讲例1 下列函数中,哪些是二次函数?并指出二次函数
的二次项系数、一次项系数和常数项.
(1)y=7x-1;(2)y=-5x2; (3)y=3a3+2a2;
(4)y=x-2+x; (5)y=3(x-2)(x-5); (6)y=x2+ .知1-讲解:(2)与(5)是二次函数.(2)y=-5x2的二次项系数为
-5,一次项系数和常数项为0;(5)化为一般式,
得到y=3x2-21x+30,所以y=3(x-2)(x-5)的
二次项系数为3,一次项系数为-21,常数项为30.知1-讲 判断一个函数是否为二次函数,即要看这个函数
的表达式化简后是否同时满足二次函数定义中的三个
条件:
(1)所表示的函数的表达式为整式;
(2)函数的表达式有唯一自变量;
(3)自变量的最高次数为2且二次项系数不等于0.知1-讲导引:若是二次函数,则等号的右边应是关于x的二次多项
式,故a-b=0,2a+b-3=0,于是a,b可求.知1-讲 当二次项系数是待定字母时,求出字母的值必须
满足二次项系数不为0这一条件.1 (2015·兰州)下列函数表达式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
2 下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+ +1
C.y=2x2-1 D.y=
3 下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0知1-练4 若函数y=(m-2)x2+4x-5(m是常数)是二次函数,
则( )
A.m≠-2 B.m≠2 C.m≠3 D.m≠-3
5 若y=(m-1)x m2+1是二次函数,则m的值是( )
A.1 B.-1 C.1或-1 D.2
6 下列结论中正确的是( )
A.二次函数中两个变量的值是非零实数
B.二次函数中变量x的值可以是所有实数
C.形如y=ax2+bx+c的函数叫二次函数
D.二次函数y=ax2+bx+c中a,b,c的值均不能为零知1-练2知识点利用二次函数的表达式表示实际问题知2-讲?1.根据实际问题列二次函数的关系式,一般要经历以下
几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关
系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
2.易错警示:一般情况下,二次函数中自变量的取值范
围是全体实数,但对实际问题的自变量的取值范围必
须使实际问题有意义.知2-讲 例3 填空:
(1)已知圆柱的高为14 cm,则圆柱的体积V(cm3)与底面半
径r(cm)之间的函数关系式是_______________;
(2)已知正方形的边长为10,若边长减少x,则面积减少y,
y与x之间的函数关系式是_____________________. (1)根据圆柱体积公式V=πr2×h求解;
(2)有三种思路:如图,①减少的面积y=
S四边形AEMG+S四边形GMFD+S四边形MHCF=x(10-x)
+x2+x(10-x)=-x2+20x,②减少的面积y=
S四边形AEFD+S四边形GHCD-S四边形GMFD=10x+10x-x2=-x2
+20x,③减少的面积y=S四边形ABCD-S四边形EBHM=102-(10
-x)2=-x2+20x.V=14πr2(r>0)y=-x2+20x(0≤x≤10)导引:知2-讲(1)求几何问题中二次函数的关系式,除了根据有关面积、体积公式
写出二次函数关系式以外,还应考虑问题的实际意义,明确自变
量的取值(在一些问题中,自变量的取值可能是整数或者是在一
定的范围内);
(2)如果不能通过已知条件直接写出函数关系式(直接法),应适当考
虑通过割补法,将问题转化为几个图形面积和差的问题(间接法),
再寻求解答;判断自变量的取值范围,应结合问题,考虑全面,
不要漏掉一些约束条件.列不等式组是求自变量的取值范围的常
见方法.
(3)如果要作实际问题中的函数的图象,注意其图象应是在自变量取
值范围内的部分图象.知2-讲例4〈易错题〉在某市开展的环境创优活动中,某居民小区要
在一块靠墙(墙长15 m)的空地上修建一个矩形花园ABCD,
花园的一边靠墙,另三边用总长为40 m的栅栏围成,若设
花园平行于墙的一边长为x m,花园的面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围.
(2)满足条件的花园的面积能达到200 m2吗?若能,求出此
时x的值,若不能,说明理由.导引:本例根据实际问题建立数学模型,转化为几何问题,
得出的有关结果要符合实际,因此列函数关系式时,
要求出自变量的取值范围.知2-讲(1)因为栅栏的总长为40 m,如图,
若BC的长为x m,则AB的长为 m.
由 可得0 根据题意,得y=x· ,即y=- x2+20x,
所以y=- x2+20x(0(2)不能.理由如下:当y=200时,- x2+20x=200,所
以x2-40x+400=0.解得x1=x2=20.因为0 花园的面积不能达到200 m2.解:知2-讲(1)此题将生活问题转化为几何问题,列生活中有关几何
面积问题的函数关系式,一般先要根据题中条件求出
自变量的取值范围,再由相关的面积公式求出函数关
系式.
(2)求自变量的取值范围,应结合问题,全面考虑,不要
漏掉一些约束条件(如本例中墙长15 m),列不等式组
是求自变量取值范围的常用方法.
(3)本例(2)中常常因不考虑自变量x的范围而出现错误结
论.1 一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价格为y万元,则y与x之间的函数表达式为( )
A.y=60(1-x)2 B.y=60(1-x)
C.y=60-x2 D.y=60(1+x)2知2-练(2015·温州)如图,∠AOB=90°,在∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH,
已知∠DFE=∠GFH=120°,FG=FE.设OC=x,
图中阴影部分的面积为y,则y与x之间的函数表达式是
( )
A.y= x2 B.y= x2
C.y=2 x2 D.y=3 x2知2-练 3 下列函数关系中,不是二次函数的是( )
A.边长为x的正方形的面积y与边长x的函数关系
B.一个直角三角形两条直角边长的和是6,则这个
直角三角形的面积y与一条直角边长x的函数关系
C.在边长为5的正方形内挖去一个边长为t的小正方
形,剩余面积S与t的函数关系
D.多边形的内角和m与边数n的函数关系知2-练1.关于二次函数的定义要理解三点:
(1)函数表达式必须是整式,自变量的取值是全体实
数,而在实际应用中,自变量的取值必须符合实
际意义.
(2)确定二次函数表达式的各项系数及常数项时,要
把函数表达式化为一般式.
(3)二次项系数不为0.2.根据实际问题列二次函数的关系式,一般要经历以下
几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关
系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
利用二次函数的表达式表示实际问题2课时流程逐点
导讲练课堂小结作业提升 某果园有100棵橙子树,平均每棵树结
600个橙子.现准备多种一些橙子树以提高果
园产量,但是如果多种树,那么树之间的距
离和每一棵树所接受的阳光就会减少.根据
经验估计,每多种一棵树,平均每棵树就会
少结5个橙子.
(1)问题中有哪些变量?其中哪些是自变量?哪些是因变量?
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式. 果园共有(100+x)棵树,平均每棵树结(600-5x)
个橙子,因此果园橙子的总产量
y=(600-5x)(100+x)=-5x2+100x+60 000.1知识点二次函数的定义做一做 银行的储蓄利率是随时间变化的,也
就是说,利率是一个变量.在我国,利率的
调整是由中国人民银行根据国民经济发展
的情况而决定的.
设人民币一年定期储蓄的年利率是x,
一年到期后,银行将本金和利息自动按一
年定期储蓄转存.如果存款额是100元,那
么请你写出两年后的本息和y(元)的表达式.知1-导知1-导 (1)两数和是20,设其中一个数是x,你能写出中两
数之积y的表达式吗?
(2)已知矩形的周长为40cm,它的面积可能是100cm2
吗?可能是75cm2吗?还可能是多少?你能表示这个矩形的
面积与其一边长的关系吗?想一想1.定义:一般地,若两个变量x,y之间的对应关系可以表示
成y=ax2+bx+c(a,b,c是常数,a≠0)的形式,则称y是x
的二次函数;其中a是二次项系数,b为一次项系数,c为
常数项.
要点精析:(1)二次函数必须满足三个条件:
①函数表达式为整式;
②函数表达式有唯一的自变量;
③自变量的最高次数是2且二次项系数不等于0.
(2)二次函数中自变量的取值范围是一切实数,函数值范围不
是一切实数.知1-讲2.判断一个函数是否为二次函数的方法:
(1)将函数表达式整理为右边是含自变量的代数式,左边是
因变量的形式;
(2)判断右边含自变量的代数式是否为整式;
(3)判断自变量的最高次数是否为2;
(4)判断二次项系数是否为0.
3.易错警示:判断一个函数是不是二次函数,化为一般形
式后当二次项系数包含字母时,一定要注意二次项的系
数不能为零这一条件.知1-讲例1 下列函数中,哪些是二次函数?并指出二次函数
的二次项系数、一次项系数和常数项.
(1)y=7x-1;(2)y=-5x2; (3)y=3a3+2a2;
(4)y=x-2+x; (5)y=3(x-2)(x-5); (6)y=x2+ .知1-讲解:(2)与(5)是二次函数.(2)y=-5x2的二次项系数为
-5,一次项系数和常数项为0;(5)化为一般式,
得到y=3x2-21x+30,所以y=3(x-2)(x-5)的
二次项系数为3,一次项系数为-21,常数项为30.知1-讲 判断一个函数是否为二次函数,即要看这个函数
的表达式化简后是否同时满足二次函数定义中的三个
条件:
(1)所表示的函数的表达式为整式;
(2)函数的表达式有唯一自变量;
(3)自变量的最高次数为2且二次项系数不等于0.知1-讲导引:若是二次函数,则等号的右边应是关于x的二次多项
式,故a-b=0,2a+b-3=0,于是a,b可求.知1-讲 当二次项系数是待定字母时,求出字母的值必须
满足二次项系数不为0这一条件.1 (2015·兰州)下列函数表达式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
2 下列各式中,y是x的二次函数的是( )
A.y= B.y=x2+ +1
C.y=2x2-1 D.y=
3 下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0知1-练4 若函数y=(m-2)x2+4x-5(m是常数)是二次函数,
则( )
A.m≠-2 B.m≠2 C.m≠3 D.m≠-3
5 若y=(m-1)x m2+1是二次函数,则m的值是( )
A.1 B.-1 C.1或-1 D.2
6 下列结论中正确的是( )
A.二次函数中两个变量的值是非零实数
B.二次函数中变量x的值可以是所有实数
C.形如y=ax2+bx+c的函数叫二次函数
D.二次函数y=ax2+bx+c中a,b,c的值均不能为零知1-练2知识点利用二次函数的表达式表示实际问题知2-讲?1.根据实际问题列二次函数的关系式,一般要经历以下
几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关
系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
2.易错警示:一般情况下,二次函数中自变量的取值范
围是全体实数,但对实际问题的自变量的取值范围必
须使实际问题有意义.知2-讲 例3 填空:
(1)已知圆柱的高为14 cm,则圆柱的体积V(cm3)与底面半
径r(cm)之间的函数关系式是_______________;
(2)已知正方形的边长为10,若边长减少x,则面积减少y,
y与x之间的函数关系式是_____________________. (1)根据圆柱体积公式V=πr2×h求解;
(2)有三种思路:如图,①减少的面积y=
S四边形AEMG+S四边形GMFD+S四边形MHCF=x(10-x)
+x2+x(10-x)=-x2+20x,②减少的面积y=
S四边形AEFD+S四边形GHCD-S四边形GMFD=10x+10x-x2=-x2
+20x,③减少的面积y=S四边形ABCD-S四边形EBHM=102-(10
-x)2=-x2+20x.V=14πr2(r>0)y=-x2+20x(0≤x≤10)导引:知2-讲(1)求几何问题中二次函数的关系式,除了根据有关面积、体积公式
写出二次函数关系式以外,还应考虑问题的实际意义,明确自变
量的取值(在一些问题中,自变量的取值可能是整数或者是在一
定的范围内);
(2)如果不能通过已知条件直接写出函数关系式(直接法),应适当考
虑通过割补法,将问题转化为几个图形面积和差的问题(间接法),
再寻求解答;判断自变量的取值范围,应结合问题,考虑全面,
不要漏掉一些约束条件.列不等式组是求自变量的取值范围的常
见方法.
(3)如果要作实际问题中的函数的图象,注意其图象应是在自变量取
值范围内的部分图象.知2-讲例4〈易错题〉在某市开展的环境创优活动中,某居民小区要
在一块靠墙(墙长15 m)的空地上修建一个矩形花园ABCD,
花园的一边靠墙,另三边用总长为40 m的栅栏围成,若设
花园平行于墙的一边长为x m,花园的面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围.
(2)满足条件的花园的面积能达到200 m2吗?若能,求出此
时x的值,若不能,说明理由.导引:本例根据实际问题建立数学模型,转化为几何问题,
得出的有关结果要符合实际,因此列函数关系式时,
要求出自变量的取值范围.知2-讲(1)因为栅栏的总长为40 m,如图,
若BC的长为x m,则AB的长为 m.
由 可得0
所以y=- x2+20x(0
以x2-40x+400=0.解得x1=x2=20.因为0
面积问题的函数关系式,一般先要根据题中条件求出
自变量的取值范围,再由相关的面积公式求出函数关
系式.
(2)求自变量的取值范围,应结合问题,全面考虑,不要
漏掉一些约束条件(如本例中墙长15 m),列不等式组
是求自变量取值范围的常用方法.
(3)本例(2)中常常因不考虑自变量x的范围而出现错误结
论.1 一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价格为y万元,则y与x之间的函数表达式为( )
A.y=60(1-x)2 B.y=60(1-x)
C.y=60-x2 D.y=60(1+x)2知2-练(2015·温州)如图,∠AOB=90°,在∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH,
已知∠DFE=∠GFH=120°,FG=FE.设OC=x,
图中阴影部分的面积为y,则y与x之间的函数表达式是
( )
A.y= x2 B.y= x2
C.y=2 x2 D.y=3 x2知2-练 3 下列函数关系中,不是二次函数的是( )
A.边长为x的正方形的面积y与边长x的函数关系
B.一个直角三角形两条直角边长的和是6,则这个
直角三角形的面积y与一条直角边长x的函数关系
C.在边长为5的正方形内挖去一个边长为t的小正方
形,剩余面积S与t的函数关系
D.多边形的内角和m与边数n的函数关系知2-练1.关于二次函数的定义要理解三点:
(1)函数表达式必须是整式,自变量的取值是全体实
数,而在实际应用中,自变量的取值必须符合实
际意义.
(2)确定二次函数表达式的各项系数及常数项时,要
把函数表达式化为一般式.
(3)二次项系数不为0.2.根据实际问题列二次函数的关系式,一般要经历以下
几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关
系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
