2.4.1 利用二次函数解决几何面积的最值问题课件
文档属性
| 名称 | 2.4.1 利用二次函数解决几何面积的最值问题课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 991.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 00:00:00 | ||
图片预览







文档简介
课件28张PPT。第二章 二次函数第4节 二次函数的应用第1课时 利用二次函数解决几
何面积的最值问题1课堂讲解二次函数的最值
几何面积的最值2课时流程逐点
导讲练课堂小结作业提升1知识点二次函数的最值1.当自变量的取值范围是全体实数时,函数在顶点处
取得最值.即当x=- 时,y最值= .
当a>0时,在顶点处取得最小值,此时不存在最大
值;当a<0时,在顶点处取得最大值,此时不存在
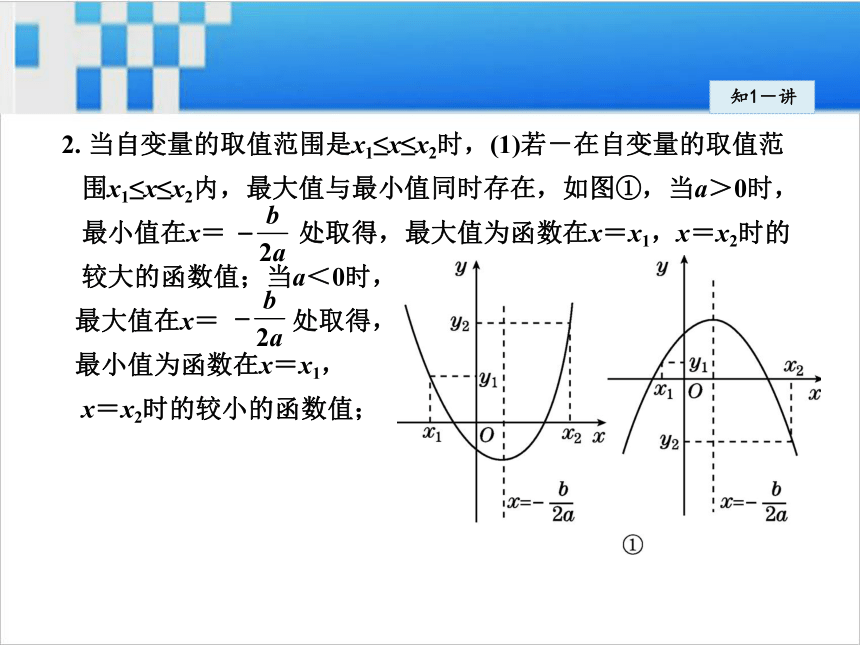
最小值.知1-讲知1-讲2. 当自变量的取值范围是x1≤x≤x2时,(1)若-在自变量的取值范
围x1≤x≤x2内,最大值与最小值同时存在,如图①,当a>0时,
最小值在x= 处取得,最大值为函数在x=x1,x=x2时的
较大的函数值;当a<0时,
最大值在x= 处取得,
最小值为函数在x=x1,
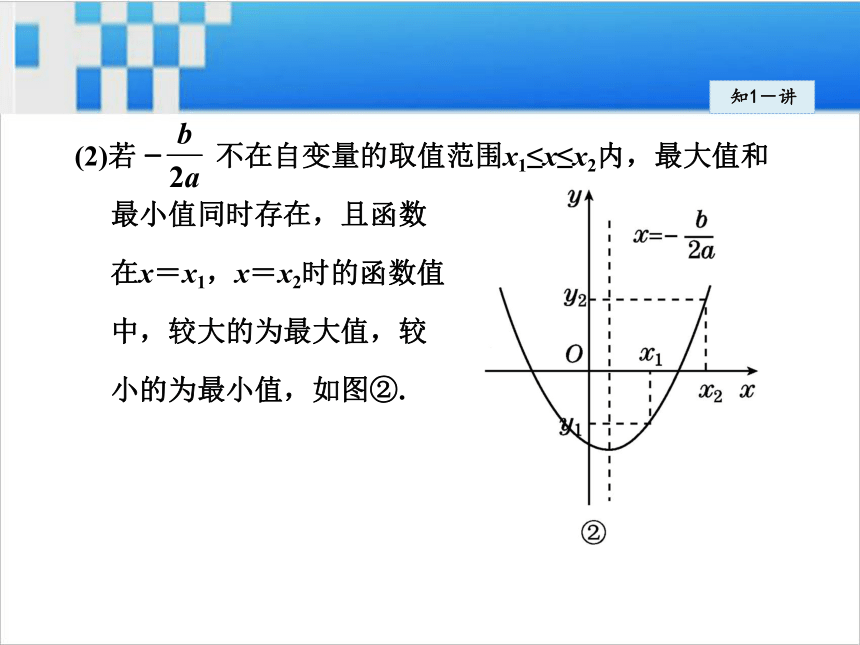
x=x2时的较小的函数值;知1-讲(2)若 不在自变量的取值范围x1≤x≤x2内,最大值和
最小值同时存在,且函数
在x=x1,x=x2时的函数值
中,较大的为最大值,较
小的为最小值,如图②.知1-讲3. 易错警示:
当二次函数自变量的取值范围是全体实数时,最值是
最大值还是最小值要根据二次项系数a的正负来确定,
当a>0时,为最小值,当a<0时,为最大值.导引:先求出抛物线y=x2-2x-3的顶点坐标,然后
看顶点的横坐标是否在所规定的自变量的取值
范围内,根据不同情况求解,也可画出图象,
利用图象求解.例1 分别在下列范围内求函数y=x2-2x-3的最值:
(1)0<x<2;(2)2≤x≤3.知1-讲解:∵y=x2-2x-3=(x-1)2-4,
∴图象的顶点坐标为(1,-4).
(1)∵x=1在0<x<2范围内,且a=1>0,
∴当x=1时,y有最小值,y最小值=-4.
∵x=1是0<x<2范围的中点,在直线x=1两侧的
图象左右对称,端点处取不到,
∴不存在最大值.知1-讲知1-讲(2)∵x=1不在2≤x≤3范围内(如图),
而函数y=x2-2x-3(2≤x≤3)的图象是抛物线
y=x2-2x-3的一部分,且当2≤x≤3时,
y随x的增大而增大,
∴当x=3时,
y最大值=32-2×3-3=0;
当x=2时,
y最小值=22-2×2-3=-3.总 结知1-讲 求函数在自变量某一取值范围内的最值,可
根据函数增减性进行讨论,或画出函数的图象,
借助于图象的直观性求解.1 二次函数y=x2-4x+c的最小值为0,则c的值
为( )
A.2 B.4 C.-4 D.16
2 已知x2+y=3,当1≤x≤2时,y的最小值是( )
A.-1 B.2 C. D.3知1-练3 已知y=-x(x+3-a)+1是关于x的二次函数,当x
的取值范围在1≤x≤5时,若y在x=1时取得最大值,
则实数a的取值情况是( )
A.a=9 B.a=5 C.a≤9 D.a≤5
4 二次函数y=2x2-6x+1,当0≤x≤5时,y的取值范
围是________________.知1-练2知识点几何面积的最值知2-导 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和CD分别在两直角边上.
(1)如果设矩形的一边AB=xm,
那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x
取何值时,y的值最大?
最大值是多少?问 题知2-讲1.利用二次函数求几何图形的面积的最值的一般步骤:
(1)引入自变量;
(2)用含有自变量的代数式分别表示与所求几何图形相
关的量;
(3)由几何图形的特征,列出其面积的计算公式,并且
用函数表示这个面积;
(4)根据函数的关系式及自变量的取值范围求出其最值.
2.易错警示:实际问题中的最大(小)值未必就是抛物线
的顶点的纵坐标.最大(小)值的取舍要结合自变量的
取值范围.知2-讲例2 某建筑物的窗户如图所示,它的上半部分是半圆,
下半部分是矩形,制造窗框的材料总长(图中所
有黑线的长度和)为15m.当x等于多少时,窗户通
过的光线最多?(结果精确到0.01m)此时,窗户的
面积是多少?(结果精确到0.01m2)知2-讲解: ∵ 7x+4y+πx=15,
设窗户的面积是Sm2,则S= πx2+2xy
当x= ≈1.07 时,S最大 = ≈4.02.
因此,当x约为1.07m时,窗户通过的光线最多.
此时,窗户的面积约为 4.02 m2.知2-讲例3 如图,已知△ABC的面积为2 400 cm2,底边BC长为80
cm.若点D在BC边上,E在AC边上,F在AB边上,且四
边形BDEF为平行四边形,设BD=
x(cm),S?BDEF=y(cm2),求:
(1)y与x之间的函数关系式.
(2)自变量x的取值范围.
(3)当x为何值时,y取得最大值?最大值是多少?导引:(1)可分别设出△DCE的边CD上的高和△ABC的边BC
上的高,根据条件求出△ABC的边BC上的高,再利用
相似找出其他等量关系,然后设法用x表示?BDEF的边
BD上的高;(2)BD在BC边上,最长不超过BC;(3)根据
x的取值范围及求最值的方法解题.知2-讲解:(1)设△DCE的边CD上的高为h cm,△ABC的边BC上的
高为b cm,则有S?BDEF=xh(cm2).
∵S△ABC= BC·b,
∴2 400= ×80b.∴b=60.
∵四边形BDEF为平行四边形,
∴DE∥AB.∴△EDC∽△ABC.
∴
∴y=x· =- x2+60x,即y=- x2+60x.
知2-讲 (2)自变量x的取值范围是0<x<80.
(3)由(1)可得y=- (x-40)2+1 200.
∵a=- <0,0<x<80,
∴当x=40时,y取得最大值,最大值是1 200. 总 结知2-讲 本题利用数形结合思想,先利用相似三角形找出
各边的关系,再代入数值,用x表示出h,进而得到y
与x之间的函数关系式,利用建模思想,建立用二次
函数求几何图形的最大面积的模型,再利用配方法求
出最大面积.知2-讲例4 〈实际应用题,易错题〉张大伯准备用一面长15 m的墙
和长38 m的栅栏修建一个如图所示的矩形养殖场ABCD,
并在养殖场的一侧留出一个2 m宽的门.
(1)求养殖场的面积y(m2)与BC边的长
x(m)之间的函数关系式.
(2)当BC边的长为多少时,养殖场的
面积最大?最大面积是多少?导引:由BC边的长和栅栏的总长可以表示出AB的长,故可求
养殖场的面积y与BC边的长x的函数关系式,再由二次
函数的有关性质和自变量的取值范围可求出养殖场的
最大面积.知2-讲解:(1)由题意得,AB= m,
∴y=x· =x· =- x2+20x.
由题意知
∴0<x≤15.∴y=- x2+20x,其中0<x≤15.
知2-讲 (2)y=- x2+20x=- (x2-40x)
=- (x-20)2+200.
∵a=- <0,0<x≤15,∴y随x的增大而增大.
∴当x=15时,y最大=- ×(15-20)2+200=187.5.
答:BC边的长为15 m时,养殖场的面积最大,最大面
积是187.5 m2.总 结知2-讲 本题利用建模思想,先由图形的面积公式建立函
数模型,最后由函数的性质在自变量的取值范围内求
出其最值.1 已知一个直角三角形两直角边长之和为20 cm,则
这个直角三角形的最大面积为( )
A.25 cm2 B.50 cm2
C.100 cm2 D.不确定
2 用一条长为40 cm的绳子围成一个面积为a cm2的长
方形,a的值不可能为( )
A.20 B.40 C.100 D.120知2-练3 如图,在矩形ABCD中,AD=1,AB=2,从较短
边AD上找一点E,过这点剪下两个正方形,它们
的边长分别是AE,DE,当剪下的两个正方形的面
积之和最小时,点E应选在( )
A.AD的中点
B.AE∶ED=( -1)∶2
C.AE∶ED= ∶1
D.AE∶ED=( -1)∶2 知2-练4 (2016·内江)某中学课外兴趣活动小组准备围建一个
矩形苗圃园,其中一边靠墙,另外三边用长为30 m
的篱笆围成,已知墙长为18 m(如图所示),设这个苗
圃园垂直于墙的一边的长为x m.
(1)若苗圃园的面积为72 m2,求x.
(2)若平行于墙的一边长不小于8 m,
这个苗圃园的面积有最大值和最小值吗?如果有,
求出最大值和最小值;如果没有,请说明理由.
(3)当这个苗圃园的面积不小于100 m2时,直接写出
x的取值范围.知2-练 利用二次函数求几何图形面积的最值是二次函数
应用的重点之一,解决此类问题的基本方法是:借助
已知条件,分析几何图形的性质,确定二次函数表达
式,再根据二次函数的图象和性质求出最值,从而解
决问题.
何面积的最值问题1课堂讲解二次函数的最值
几何面积的最值2课时流程逐点
导讲练课堂小结作业提升1知识点二次函数的最值1.当自变量的取值范围是全体实数时,函数在顶点处
取得最值.即当x=- 时,y最值= .
当a>0时,在顶点处取得最小值,此时不存在最大
值;当a<0时,在顶点处取得最大值,此时不存在
最小值.知1-讲知1-讲2. 当自变量的取值范围是x1≤x≤x2时,(1)若-在自变量的取值范
围x1≤x≤x2内,最大值与最小值同时存在,如图①,当a>0时,
最小值在x= 处取得,最大值为函数在x=x1,x=x2时的
较大的函数值;当a<0时,
最大值在x= 处取得,
最小值为函数在x=x1,
x=x2时的较小的函数值;知1-讲(2)若 不在自变量的取值范围x1≤x≤x2内,最大值和
最小值同时存在,且函数
在x=x1,x=x2时的函数值
中,较大的为最大值,较
小的为最小值,如图②.知1-讲3. 易错警示:
当二次函数自变量的取值范围是全体实数时,最值是
最大值还是最小值要根据二次项系数a的正负来确定,
当a>0时,为最小值,当a<0时,为最大值.导引:先求出抛物线y=x2-2x-3的顶点坐标,然后
看顶点的横坐标是否在所规定的自变量的取值
范围内,根据不同情况求解,也可画出图象,
利用图象求解.例1 分别在下列范围内求函数y=x2-2x-3的最值:
(1)0<x<2;(2)2≤x≤3.知1-讲解:∵y=x2-2x-3=(x-1)2-4,
∴图象的顶点坐标为(1,-4).
(1)∵x=1在0<x<2范围内,且a=1>0,
∴当x=1时,y有最小值,y最小值=-4.
∵x=1是0<x<2范围的中点,在直线x=1两侧的
图象左右对称,端点处取不到,
∴不存在最大值.知1-讲知1-讲(2)∵x=1不在2≤x≤3范围内(如图),
而函数y=x2-2x-3(2≤x≤3)的图象是抛物线
y=x2-2x-3的一部分,且当2≤x≤3时,
y随x的增大而增大,
∴当x=3时,
y最大值=32-2×3-3=0;
当x=2时,
y最小值=22-2×2-3=-3.总 结知1-讲 求函数在自变量某一取值范围内的最值,可
根据函数增减性进行讨论,或画出函数的图象,
借助于图象的直观性求解.1 二次函数y=x2-4x+c的最小值为0,则c的值
为( )
A.2 B.4 C.-4 D.16
2 已知x2+y=3,当1≤x≤2时,y的最小值是( )
A.-1 B.2 C. D.3知1-练3 已知y=-x(x+3-a)+1是关于x的二次函数,当x
的取值范围在1≤x≤5时,若y在x=1时取得最大值,
则实数a的取值情况是( )
A.a=9 B.a=5 C.a≤9 D.a≤5
4 二次函数y=2x2-6x+1,当0≤x≤5时,y的取值范
围是________________.知1-练2知识点几何面积的最值知2-导 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和CD分别在两直角边上.
(1)如果设矩形的一边AB=xm,
那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x
取何值时,y的值最大?
最大值是多少?问 题知2-讲1.利用二次函数求几何图形的面积的最值的一般步骤:
(1)引入自变量;
(2)用含有自变量的代数式分别表示与所求几何图形相
关的量;
(3)由几何图形的特征,列出其面积的计算公式,并且
用函数表示这个面积;
(4)根据函数的关系式及自变量的取值范围求出其最值.
2.易错警示:实际问题中的最大(小)值未必就是抛物线
的顶点的纵坐标.最大(小)值的取舍要结合自变量的
取值范围.知2-讲例2 某建筑物的窗户如图所示,它的上半部分是半圆,
下半部分是矩形,制造窗框的材料总长(图中所
有黑线的长度和)为15m.当x等于多少时,窗户通
过的光线最多?(结果精确到0.01m)此时,窗户的
面积是多少?(结果精确到0.01m2)知2-讲解: ∵ 7x+4y+πx=15,
设窗户的面积是Sm2,则S= πx2+2xy
当x= ≈1.07 时,S最大 = ≈4.02.
因此,当x约为1.07m时,窗户通过的光线最多.
此时,窗户的面积约为 4.02 m2.知2-讲例3 如图,已知△ABC的面积为2 400 cm2,底边BC长为80
cm.若点D在BC边上,E在AC边上,F在AB边上,且四
边形BDEF为平行四边形,设BD=
x(cm),S?BDEF=y(cm2),求:
(1)y与x之间的函数关系式.
(2)自变量x的取值范围.
(3)当x为何值时,y取得最大值?最大值是多少?导引:(1)可分别设出△DCE的边CD上的高和△ABC的边BC
上的高,根据条件求出△ABC的边BC上的高,再利用
相似找出其他等量关系,然后设法用x表示?BDEF的边
BD上的高;(2)BD在BC边上,最长不超过BC;(3)根据
x的取值范围及求最值的方法解题.知2-讲解:(1)设△DCE的边CD上的高为h cm,△ABC的边BC上的
高为b cm,则有S?BDEF=xh(cm2).
∵S△ABC= BC·b,
∴2 400= ×80b.∴b=60.
∵四边形BDEF为平行四边形,
∴DE∥AB.∴△EDC∽△ABC.
∴
∴y=x· =- x2+60x,即y=- x2+60x.
知2-讲 (2)自变量x的取值范围是0<x<80.
(3)由(1)可得y=- (x-40)2+1 200.
∵a=- <0,0<x<80,
∴当x=40时,y取得最大值,最大值是1 200. 总 结知2-讲 本题利用数形结合思想,先利用相似三角形找出
各边的关系,再代入数值,用x表示出h,进而得到y
与x之间的函数关系式,利用建模思想,建立用二次
函数求几何图形的最大面积的模型,再利用配方法求
出最大面积.知2-讲例4 〈实际应用题,易错题〉张大伯准备用一面长15 m的墙
和长38 m的栅栏修建一个如图所示的矩形养殖场ABCD,
并在养殖场的一侧留出一个2 m宽的门.
(1)求养殖场的面积y(m2)与BC边的长
x(m)之间的函数关系式.
(2)当BC边的长为多少时,养殖场的
面积最大?最大面积是多少?导引:由BC边的长和栅栏的总长可以表示出AB的长,故可求
养殖场的面积y与BC边的长x的函数关系式,再由二次
函数的有关性质和自变量的取值范围可求出养殖场的
最大面积.知2-讲解:(1)由题意得,AB= m,
∴y=x· =x· =- x2+20x.
由题意知
∴0<x≤15.∴y=- x2+20x,其中0<x≤15.
知2-讲 (2)y=- x2+20x=- (x2-40x)
=- (x-20)2+200.
∵a=- <0,0<x≤15,∴y随x的增大而增大.
∴当x=15时,y最大=- ×(15-20)2+200=187.5.
答:BC边的长为15 m时,养殖场的面积最大,最大面
积是187.5 m2.总 结知2-讲 本题利用建模思想,先由图形的面积公式建立函
数模型,最后由函数的性质在自变量的取值范围内求
出其最值.1 已知一个直角三角形两直角边长之和为20 cm,则
这个直角三角形的最大面积为( )
A.25 cm2 B.50 cm2
C.100 cm2 D.不确定
2 用一条长为40 cm的绳子围成一个面积为a cm2的长
方形,a的值不可能为( )
A.20 B.40 C.100 D.120知2-练3 如图,在矩形ABCD中,AD=1,AB=2,从较短
边AD上找一点E,过这点剪下两个正方形,它们
的边长分别是AE,DE,当剪下的两个正方形的面
积之和最小时,点E应选在( )
A.AD的中点
B.AE∶ED=( -1)∶2
C.AE∶ED= ∶1
D.AE∶ED=( -1)∶2 知2-练4 (2016·内江)某中学课外兴趣活动小组准备围建一个
矩形苗圃园,其中一边靠墙,另外三边用长为30 m
的篱笆围成,已知墙长为18 m(如图所示),设这个苗
圃园垂直于墙的一边的长为x m.
(1)若苗圃园的面积为72 m2,求x.
(2)若平行于墙的一边长不小于8 m,
这个苗圃园的面积有最大值和最小值吗?如果有,
求出最大值和最小值;如果没有,请说明理由.
(3)当这个苗圃园的面积不小于100 m2时,直接写出
x的取值范围.知2-练 利用二次函数求几何图形面积的最值是二次函数
应用的重点之一,解决此类问题的基本方法是:借助
已知条件,分析几何图形的性质,确定二次函数表达
式,再根据二次函数的图象和性质求出最值,从而解
决问题.
