2.4.2 利用建立坐标系解决“抛物线”型最值问题课件
文档属性
| 名称 | 2.4.2 利用建立坐标系解决“抛物线”型最值问题课件 |  | |
| 格式 | zip | ||
| 文件大小 | 935.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 20:06:51 | ||
图片预览







文档简介
课件25张PPT。第二章 二次函数第4节 二次函数的应用第2课时 利用建立坐标系解决“抛
物线”型最值问题1课堂讲解建立坐标系解抛物线型建筑问题
建立坐标系解抛物线型运动问题2课时流程逐点
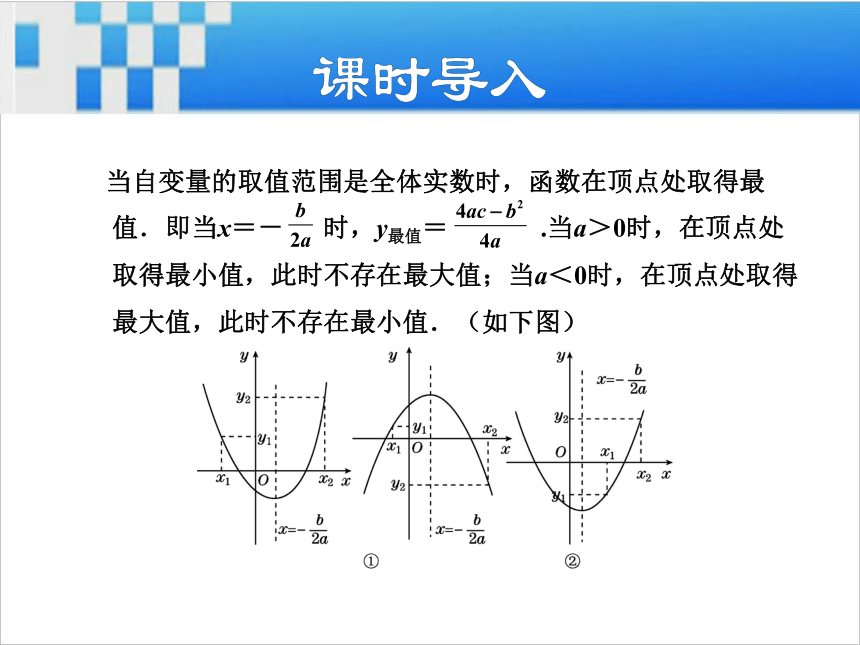
导讲练课堂小结作业提升 当自变量的取值范围是全体实数时,函数在顶点处取得最
值.即当x=- 时,y最值= .当a>0时,在顶点处
取得最小值,此时不存在最大值;当a<0时,在顶点处取得
最大值,此时不存在最小值.(如下图)1知识点建立坐标系解抛物线型建筑问题知1-讲1.运用二次函数的代数模型解决实际中的问题,如抛
(投)物体,抛物线的模型问题等,经常需要运用抽象
与概括的数学思想,将文字语言转化为数学符号.
2.利用二次函数解决实际问题的基本思路是:
(1)建立适当的平面直角坐标系;
(2)把实际问题中一些数据与点的坐标联系起来;
(3)用待定系数法求出抛物线对应的函数表达式;
(4)利用二次函数的图象及性质去分析、解决问题.知1-讲3.易错警示:
(1)利用二次函数求最值,对于实际问题中的最值,
要注意自变量的取值范围.
(2)建立平面直角坐标系时,要遵循以下两个原则:
①所建立的坐标系能使求出的二次函数表达式比较
简单;
②根据已知点所在位置建立坐标系求函数表达式比
较简单.导引:由题意可知拱桥为抛物线型,因此可建立以O为坐标原
点,AB所在直线为x轴,OC所在直线为y轴的直角坐标
系,利用二次函数y=ax2+c 解决问题.例1 〈乌鲁木齐〉如图是一个抛物线型拱桥的示意图,桥的
跨度AB为100 m,支撑桥的是一些等距的立柱,相邻立
柱间的水平距离均为10 m(不考虑立柱的粗细),其中距
A点10 m处的立柱FE的高度为3.6 m.
(1)求正中间的立柱OC的高度.
(2)是否存在一根立柱,其高度恰
好是OC的一半?请说明理由.知1-讲知1-讲 (1)根据题意可得正中间立柱OC经过AB的中点O,如图,
以O点为坐标原点,AB所在直线为x轴,OC所在直线为y
轴,建立直角坐标系,则B点的坐标为(50,0).
∵OF=OA-FA=40 m,∴E点的坐标为(-40,3.6).
由题意可设抛物线对应的函数表达式为y=ax2+c,
∴y=- x2+10. 当x=0时,y=10,
即正中间的立柱OC的高度是10 m.解:知1-讲(2)不存在.
理由:假设存在一根立柱的高度是OC的一半,即这
根立柱的高度是5 m,则有5=- x2+10,
解得x=±25 .由题意知相邻立柱间的水平距离均
为10 m,正中间的立柱OC在y轴上,
∴每根立柱上的点的横坐标均为10的整数倍.
∴x=±25 与题意不符.
∴不存在一根立柱,其高度恰好是OC的一半.知1-讲 本题运用待定系数法求二次函数y=ax2+
c的表达式.1 (2015·铜仁)河北省赵县的赵州桥的桥拱是近似的抛
物线型,建立如图所示的平面直角坐标系,其函数
表达式为 y=- x2,当水面离桥拱顶的高度DO
是4 m时,这时水面宽度AB为( )
A.-20 m B.10 m C.20 m D.-10 m知1-练2 (2015·金华)图②是图①中拱形大桥的示意图,桥拱
与桥面的交点为O,B,以点O为原点,水平直线OB
为x轴,建立平面直角坐标系,桥的拱形可近似看成
抛物线y=- (x-80)2+16,桥拱与桥墩AC的交
点C恰好在水面,有AC⊥x轴,若OA=10 m,则桥面
离水面的高度AC为( ) ?
A.16 m B. m
C.16 m D. m知1-练例2 某公园有一个抛物线形状的观景拱桥ABC,其横截面如
图所示,在图中建立的直角坐标系中,抛物线对应的函
数表达式为y=- x2+c且过点C(0,5).(长度单位:m)
(1)直接写出c的值;
(2)现因做庆典活动,计划沿拱桥的
台阶表面铺设一条宽度为1.5 m的地
毯,地毯的价格为20元/m2,求购买地毯需多少元;
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H,
G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形
EFGH的周长为27.5 m,求斜面EG的倾斜角∠GEF的度
数.(精确到0.1°)知1-讲导引:(1)将点C的坐标代入计算即可;(2)首先应求出铺设
地毯的台阶的表面积,而求表面积的关键在于求得
所有台阶的水平和竖直的总长度,进而求得所需钱
数;(3)求出点G的坐标,在Rt△EFG中,利用三角
函数求∠GEF的度数.
解:(1)c=5.
(2)由(1)知OC=5.令y=0,即- x2+5=0,
解得x1=10,x2=-10.
∴地毯的总长度为AB+2OC=20+2×5=30(m).
∴30×1.5×20=900(元).
∴购买地毯需要900元.知1-讲(3)可设G的坐标为 其中a>0,
则EF=2a m,GF=
由已知得2(EF+GF)=27.5 m,即2
解得a1=5,a2=35(不合题意,舍去).当a=5时,
+5=- ×52+5=3.75,∴点G的坐标是(5,3.75).
∴EF=10 m,GF=3.75 m.在Rt△EFG中,tan ∠GEF=
0.375,∴∠GEF≈20.6°.知1-讲知1-讲 本题实际上是一道函数与几何的综合题.主要考
查根据题意和已知图形,利用数形结合思想、方程思
想等来解决问题,是中等难度的试题.3 (中考·绍兴)如图的一座拱桥,当水面宽AB为12 m时,
桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以
水平方向为x轴,建立平面直角坐标系,若选取点A为
坐标原点时抛物线对应的函数表达式是y=- (x-
6)2+4,则选取点B为坐标原点时抛物线对应的函数
表达式是______________________.知1-练2知识点建立坐标系解抛物线型运动问题知2-讲例3 〈一题多解〉如图,某灌溉设备的喷
头B高出地面1.25 m,喷出的抛物线
型水流在与喷头底部A的距离为1 m
处达到距离地面最大高度2.25 m,试
建立恰当的直角坐标系并求出与该抛物线型水流对应
的二次函数关系式.导引:解决问题的关键是建立适当的平面直角坐标系,把
实际问题中的长度转化为点的坐标,从而利用待定
系数法求二次函数关系式.知2-讲解:方法一:建立如图所示的平面直角坐标系,则抛物
线的顶点为O(0,0),且经过点B(-1,-1).于是
设所求二次函数关系式为y=ax2,
则有-1=a·(-1)2,得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2.知2-讲方法二:建立如图所示的平面直角坐标系,则抛物线的
顶点为D(0,2.25),且抛物线经过点B(-1,1.25).于是
设所求二次函数关系式为y=ax2+2.25,则有1.25=a·
(-1)2+2.25,解得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2+2.25.知2-讲方法三:建立如图所示的平面直角坐标系,则抛物线的
顶点为D(1,2.25),且经过点B(0,1.25).于是设所求二
次函数关系式为y=a(x-1)2+2.25,则有1.25=a(-1)2+
2.25,解得a=-1.∴抛物线型水流对应的二次函数关系
式为y=-(x-1)2+2.25.知2-讲解决抛物线型问题,其一般步骤为:
(1)建立适当的坐标系,正确写出关键点的坐标;
(2)根据图象设抛物线对应的函数表达式;
(3)根据已知条件,利用待定系数法求表达式,再利用
二次函数的性质解题.在解题过程中要充分利用抛
物线的对称性,同时要注意数形结合思想的应用.1 某广场有一喷水池,水从地面喷出,如图,以水平
地面为x轴,出水点为原点,建立平面直角坐标系,
水在空中划出的曲线是抛物线y=-x2+4x(单位:m)
的一部分,则水喷出的最大高度是( )
A.4 m
B.5 m
C.6 m
D.7 m知2-练2 小敏在某次投篮中,球的运动路线是抛物线y=- x2
+3.5的一部分(如图),若命中篮筐中心,则他与篮底
的水平距离l是( )
A.3.5 m
B.4 m
C.4.5 m
D.4.6 m知2-练3 向上发射一枚炮弹,经x s后的高度为y m,且时间与
高度之间的关系为y=ax2+bx.若此炮弹在第7 s与第
14 s时的高度相等,则在下列哪一个时间的高度是最
高的( )
A.第9.5 s B.第10 s
C.第10.5 s D.第11 s知2-练1.抛物线型建筑物问题:几种常见的抛物线型建筑物有拱形
桥洞、隧道洞口、拱形门等.解决这类问题的关键是根据
已知条件选择合理的位置建立直角坐标系,结合问题中的
数据求出函数表达式,然后利用函数表达式解决问题.
2.运动问题:(1)运动中的距离、时间、速度问题;这类问题
多根据运动规律中的公式求解.(2)物体的运动路线(轨迹)
问题;解决这类问题的思想方法是利用数形结合思想和函
数思想,合理建立直角坐标系,根据已知数据,运用待定
系数法求出运动轨迹(抛物线)对应的函数表达式,再利用
二次函数的性质去分析、解决问题.
物线”型最值问题1课堂讲解建立坐标系解抛物线型建筑问题
建立坐标系解抛物线型运动问题2课时流程逐点
导讲练课堂小结作业提升 当自变量的取值范围是全体实数时,函数在顶点处取得最
值.即当x=- 时,y最值= .当a>0时,在顶点处
取得最小值,此时不存在最大值;当a<0时,在顶点处取得
最大值,此时不存在最小值.(如下图)1知识点建立坐标系解抛物线型建筑问题知1-讲1.运用二次函数的代数模型解决实际中的问题,如抛
(投)物体,抛物线的模型问题等,经常需要运用抽象
与概括的数学思想,将文字语言转化为数学符号.
2.利用二次函数解决实际问题的基本思路是:
(1)建立适当的平面直角坐标系;
(2)把实际问题中一些数据与点的坐标联系起来;
(3)用待定系数法求出抛物线对应的函数表达式;
(4)利用二次函数的图象及性质去分析、解决问题.知1-讲3.易错警示:
(1)利用二次函数求最值,对于实际问题中的最值,
要注意自变量的取值范围.
(2)建立平面直角坐标系时,要遵循以下两个原则:
①所建立的坐标系能使求出的二次函数表达式比较
简单;
②根据已知点所在位置建立坐标系求函数表达式比
较简单.导引:由题意可知拱桥为抛物线型,因此可建立以O为坐标原
点,AB所在直线为x轴,OC所在直线为y轴的直角坐标
系,利用二次函数y=ax2+c 解决问题.例1 〈乌鲁木齐〉如图是一个抛物线型拱桥的示意图,桥的
跨度AB为100 m,支撑桥的是一些等距的立柱,相邻立
柱间的水平距离均为10 m(不考虑立柱的粗细),其中距
A点10 m处的立柱FE的高度为3.6 m.
(1)求正中间的立柱OC的高度.
(2)是否存在一根立柱,其高度恰
好是OC的一半?请说明理由.知1-讲知1-讲 (1)根据题意可得正中间立柱OC经过AB的中点O,如图,
以O点为坐标原点,AB所在直线为x轴,OC所在直线为y
轴,建立直角坐标系,则B点的坐标为(50,0).
∵OF=OA-FA=40 m,∴E点的坐标为(-40,3.6).
由题意可设抛物线对应的函数表达式为y=ax2+c,
∴y=- x2+10. 当x=0时,y=10,
即正中间的立柱OC的高度是10 m.解:知1-讲(2)不存在.
理由:假设存在一根立柱的高度是OC的一半,即这
根立柱的高度是5 m,则有5=- x2+10,
解得x=±25 .由题意知相邻立柱间的水平距离均
为10 m,正中间的立柱OC在y轴上,
∴每根立柱上的点的横坐标均为10的整数倍.
∴x=±25 与题意不符.
∴不存在一根立柱,其高度恰好是OC的一半.知1-讲 本题运用待定系数法求二次函数y=ax2+
c的表达式.1 (2015·铜仁)河北省赵县的赵州桥的桥拱是近似的抛
物线型,建立如图所示的平面直角坐标系,其函数
表达式为 y=- x2,当水面离桥拱顶的高度DO
是4 m时,这时水面宽度AB为( )
A.-20 m B.10 m C.20 m D.-10 m知1-练2 (2015·金华)图②是图①中拱形大桥的示意图,桥拱
与桥面的交点为O,B,以点O为原点,水平直线OB
为x轴,建立平面直角坐标系,桥的拱形可近似看成
抛物线y=- (x-80)2+16,桥拱与桥墩AC的交
点C恰好在水面,有AC⊥x轴,若OA=10 m,则桥面
离水面的高度AC为( ) ?
A.16 m B. m
C.16 m D. m知1-练例2 某公园有一个抛物线形状的观景拱桥ABC,其横截面如
图所示,在图中建立的直角坐标系中,抛物线对应的函
数表达式为y=- x2+c且过点C(0,5).(长度单位:m)
(1)直接写出c的值;
(2)现因做庆典活动,计划沿拱桥的
台阶表面铺设一条宽度为1.5 m的地
毯,地毯的价格为20元/m2,求购买地毯需多少元;
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H,
G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形
EFGH的周长为27.5 m,求斜面EG的倾斜角∠GEF的度
数.(精确到0.1°)知1-讲导引:(1)将点C的坐标代入计算即可;(2)首先应求出铺设
地毯的台阶的表面积,而求表面积的关键在于求得
所有台阶的水平和竖直的总长度,进而求得所需钱
数;(3)求出点G的坐标,在Rt△EFG中,利用三角
函数求∠GEF的度数.
解:(1)c=5.
(2)由(1)知OC=5.令y=0,即- x2+5=0,
解得x1=10,x2=-10.
∴地毯的总长度为AB+2OC=20+2×5=30(m).
∴30×1.5×20=900(元).
∴购买地毯需要900元.知1-讲(3)可设G的坐标为 其中a>0,
则EF=2a m,GF=
由已知得2(EF+GF)=27.5 m,即2
解得a1=5,a2=35(不合题意,舍去).当a=5时,
+5=- ×52+5=3.75,∴点G的坐标是(5,3.75).
∴EF=10 m,GF=3.75 m.在Rt△EFG中,tan ∠GEF=
0.375,∴∠GEF≈20.6°.知1-讲知1-讲 本题实际上是一道函数与几何的综合题.主要考
查根据题意和已知图形,利用数形结合思想、方程思
想等来解决问题,是中等难度的试题.3 (中考·绍兴)如图的一座拱桥,当水面宽AB为12 m时,
桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以
水平方向为x轴,建立平面直角坐标系,若选取点A为
坐标原点时抛物线对应的函数表达式是y=- (x-
6)2+4,则选取点B为坐标原点时抛物线对应的函数
表达式是______________________.知1-练2知识点建立坐标系解抛物线型运动问题知2-讲例3 〈一题多解〉如图,某灌溉设备的喷
头B高出地面1.25 m,喷出的抛物线
型水流在与喷头底部A的距离为1 m
处达到距离地面最大高度2.25 m,试
建立恰当的直角坐标系并求出与该抛物线型水流对应
的二次函数关系式.导引:解决问题的关键是建立适当的平面直角坐标系,把
实际问题中的长度转化为点的坐标,从而利用待定
系数法求二次函数关系式.知2-讲解:方法一:建立如图所示的平面直角坐标系,则抛物
线的顶点为O(0,0),且经过点B(-1,-1).于是
设所求二次函数关系式为y=ax2,
则有-1=a·(-1)2,得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2.知2-讲方法二:建立如图所示的平面直角坐标系,则抛物线的
顶点为D(0,2.25),且抛物线经过点B(-1,1.25).于是
设所求二次函数关系式为y=ax2+2.25,则有1.25=a·
(-1)2+2.25,解得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2+2.25.知2-讲方法三:建立如图所示的平面直角坐标系,则抛物线的
顶点为D(1,2.25),且经过点B(0,1.25).于是设所求二
次函数关系式为y=a(x-1)2+2.25,则有1.25=a(-1)2+
2.25,解得a=-1.∴抛物线型水流对应的二次函数关系
式为y=-(x-1)2+2.25.知2-讲解决抛物线型问题,其一般步骤为:
(1)建立适当的坐标系,正确写出关键点的坐标;
(2)根据图象设抛物线对应的函数表达式;
(3)根据已知条件,利用待定系数法求表达式,再利用
二次函数的性质解题.在解题过程中要充分利用抛
物线的对称性,同时要注意数形结合思想的应用.1 某广场有一喷水池,水从地面喷出,如图,以水平
地面为x轴,出水点为原点,建立平面直角坐标系,
水在空中划出的曲线是抛物线y=-x2+4x(单位:m)
的一部分,则水喷出的最大高度是( )
A.4 m
B.5 m
C.6 m
D.7 m知2-练2 小敏在某次投篮中,球的运动路线是抛物线y=- x2
+3.5的一部分(如图),若命中篮筐中心,则他与篮底
的水平距离l是( )
A.3.5 m
B.4 m
C.4.5 m
D.4.6 m知2-练3 向上发射一枚炮弹,经x s后的高度为y m,且时间与
高度之间的关系为y=ax2+bx.若此炮弹在第7 s与第
14 s时的高度相等,则在下列哪一个时间的高度是最
高的( )
A.第9.5 s B.第10 s
C.第10.5 s D.第11 s知2-练1.抛物线型建筑物问题:几种常见的抛物线型建筑物有拱形
桥洞、隧道洞口、拱形门等.解决这类问题的关键是根据
已知条件选择合理的位置建立直角坐标系,结合问题中的
数据求出函数表达式,然后利用函数表达式解决问题.
2.运动问题:(1)运动中的距离、时间、速度问题;这类问题
多根据运动规律中的公式求解.(2)物体的运动路线(轨迹)
问题;解决这类问题的思想方法是利用数形结合思想和函
数思想,合理建立直角坐标系,根据已知数据,运用待定
系数法求出运动轨迹(抛物线)对应的函数表达式,再利用
二次函数的性质去分析、解决问题.
