2.5.1 二次函数与一元二次方程间的关系课件
文档属性
| 名称 | 2.5.1 二次函数与一元二次方程间的关系课件 |  | |
| 格式 | zip | ||
| 文件大小 | 936.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-21 20:08:02 | ||
图片预览







文档简介
课件20张PPT。第二章 二次函数第5节 二次函数与一元二次方程第1课时 二次函数与一元二
次方程间的关系1课堂讲解二次函数与一元二次方程间的关系
二次函数与其图象与x轴的交点个数之间的关系2课时流程逐点
导讲练课堂小结作业提升 一元二次方程根的判别式:
式子b2-4ac叫做方程ax2+bx+c=0(a≠0)根的判别式,通
常用希腊字母Δ表示.
(1)当Δ>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根.
(2)当Δ=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根.
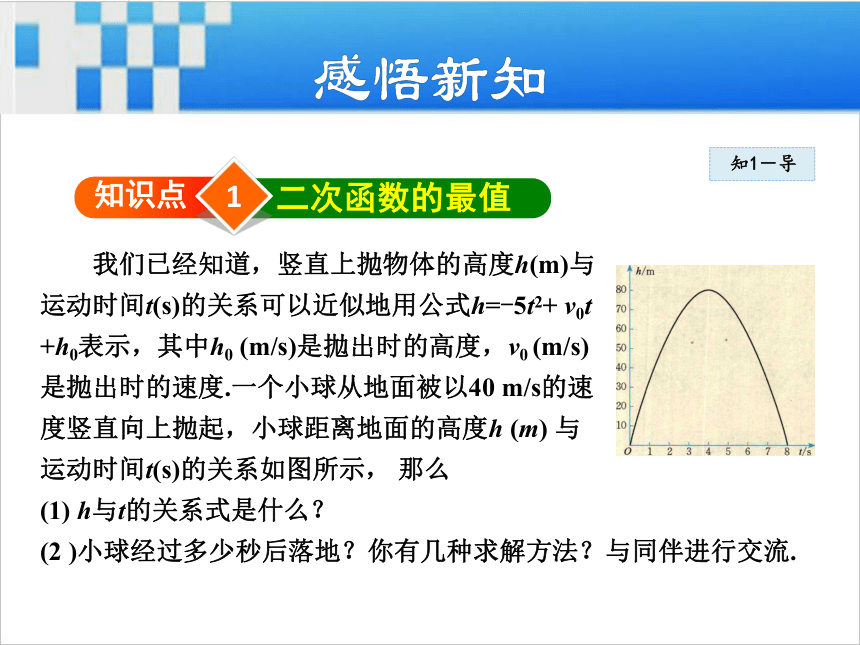
(3)当Δ<0时,方程ax2+bx+c=0(a≠0)无实数根.1知识点二次函数的最值 我们已经知道,竖直上抛物体的高度h(m)与
运动时间t(s)的关系可以近似地用公式h=-5t2+ v0t
+h0表示,其中h0 (m/s)是拋出时的高度,v0 (m/s)
是抛出时的速度.一个小球从地面被以40 m/s的速
度竖直向上抛起,小球距离地面的高度h (m) 与
运动时间t(s)的关系如图所示, 那么
(1) h与t的关系式是什么?
(2 )小球经过多少秒后落地?你有几种求解方法?与同伴进行交流.知1-导知1-讲 当二次函数y=ax2+bx+c(a≠0)的y值为0时,
就得到一元二次方程ax2+bx+c=0 .导引:要求抛物线y=3x2-8x+4与x轴的公共点坐标即需
求y=0时对应的x的值;可令y=0,根据3x2-8x+
4=0的根来确定抛物线与x轴的公共点的横坐标.
解:令y=0 , 则3x2-8x+4=0 , 解方程得:x1= , x2=2.
∴抛物线y=3x2-8x+4与x轴的两个公共点的坐标
为 ,(2,0).例1 求抛物线y=3x2-8x+4与x轴的两个公共点的坐标.知1-讲知1-讲 本例将求抛物线与x轴的公共点这个几何
问题转化为求一元二次方程的根的问题来解决,
它充分体现了由形到数的转化思想.1 抛物线y=-3(x-2)(x+5)与x轴的交点坐标为_______.
一元二次方程-3(x-2)(x+5)=0的解为____________.
2 (2016·永州)抛物线y=x2+2x+m-1与x轴有两个不同的
交点,则m的取值范围是( )
A.m<2 B.m>2
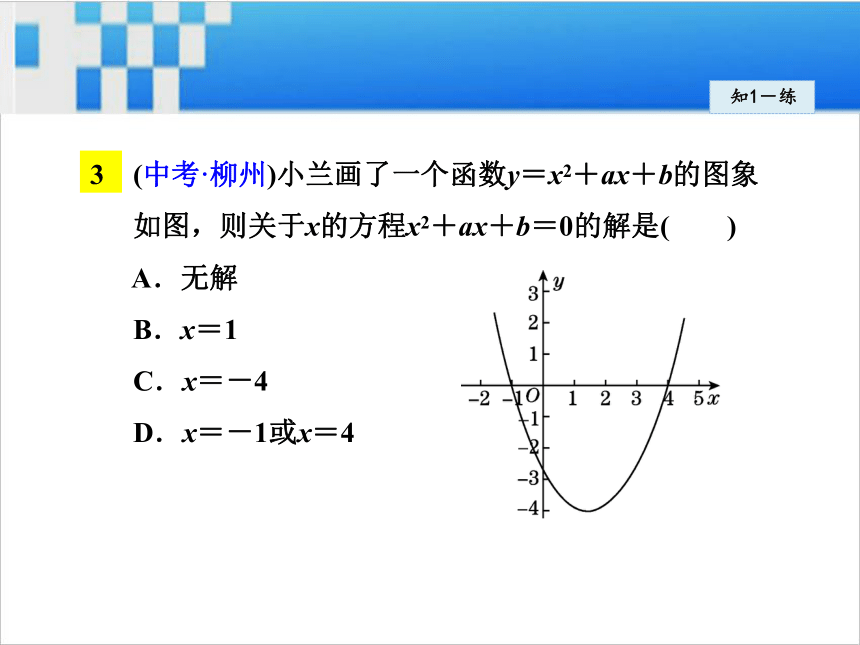
C.0<m≤2 D.m<-2知1-练3 (中考·柳州)小兰画了一个函数y=x2+ax+b的图象
如图,则关于x的方程x2+ax+b=0的解是( )
A.无解
B.x=1
C.x=-4
D.x=-1或x=4知1-练2知识点二次函数与其图象与x轴的交点个数之间的关系知2-导 二次函数y=x2+2x, y=x2-2x+1,y=x2-2x+2的图象如图所示.
(1)每个图象与x轴有几个交点?
(2) 一元二次方程x2+2x=0, x2-2x+1=0有几个实数根?用判别
式验证一下.一元二次方程
x2-2x+2=0有实数根吗?
(3)二次函数y=ax2+bx+c的图象
与x轴交点的坐标和一元二
次方程ax2+bx+c=0的根有什么关系?知2-导 二次函数y=ax2+bx+c的图象与x轴的交点有三种情
况:有两个交点、有一个交点、没有交点.
与此相对应,一元二次方程ax2+bx+c=0的根也有
三种情况:有两个不相等的实数根、有两个相等的实
数根、没有实数根.
二次函数y=ax2+bx+c的图象与x轴交点的横坐标就
是一元二次方程ax2+bx+c=0的根.知2-讲 当二次函数y=ax2+bx+c(a≠0)的y值为0时,就得到一元二
次方程ax2+bx+c=0 ,抛物线y=ax2+bx+c与x轴是否有
公共点取决于一元二次方程ax2+bx+c=0的根的情况.
(1)当b2-4ac >0时,方程有两个不相等的实数根,抛物线与x
轴有2个公共点;
(2)当b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴
有1个公共点;
(3)当b2-4ac<0时,方程没有实数根,抛物线与x轴没有公
共点.
反之亦成立.知2-讲拓展:
(1)若一元二次方程ax2+bx+c=0有两个解,且解为
x1,x2,则将多项式ax2+bx+c分解因式得a(x-x1)(x-x2),
所以二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点
(x1,0),(x2,0),函数表达式可表示为y=a(x-x1)·(x-
x2),我们称这种表达式为交点式.
(2)二次函数y=ax2+bx+c的图象与直线y=kx+m的交点坐
标就是方程组 的解,方程组若有两个解,
则两个函数的图象就有两个交点;若有一个解,则两个函
数的图象就只有一个交点;若没有解,则没有交点.知2-讲(3)如果二次函数y=ax2+bx+c的图象与x轴有两个公共点
A(m,0),B(n,0),令m= ,n= ,其中
Δ=b2-4ac.此时A,B两点间的距离
AB=
我们把AB= 叫做抛物线y=ax2+bx+c在x轴上的截距.知2-讲例2 〈荆门改编〉若抛物线y=x2+bx+c与x轴只有一个公
共点,且过点A(m,n),B(m+6,n),则n=_____.导引:∵抛物线y=x2+bx+c与x轴只有一个公共点,∴当x
=- 时,y=0,且b2-4c=0,即b2=4c.又∵抛物
线过点A(m,n),B(m+6,n),∴点A,B关于直线x
=- 对称.
将A点坐标代入抛物线对应的函数表达式,得n=
+c=- b2+c+9,∵b2=4c,
∴n=- ×4c+c+9=9.9知2-讲(1)根据二次函数的图象与x轴的公共点情况可以判断
一元二次方程的根的情况;反之,根据一元二次方
程的根的情况,可以判断二次函数的图象与x轴的
公共点的情况;
(2)拓展:一元二次方程的根的情况由根的判别式定,
二次函数的图象与x轴两公共点间的距离为 ,并
且两公共点关于直线x=- 对称.1 下列抛物线中,与x轴有两个交点的是( )
A.y=3x2-5x+3 B.y=4x2-12x+9
C.y=x2-2x+3 D.y=2x2+3x-4
2 (2016·滨州)抛物线y=2x2-2 x+1与坐标轴的交
点个数是( )
A.0 B.1 C.2 D.3知2-练3 (2015·烟台)如图,已知顶点为(-3,-6)的抛物线
y=ax2+bx+c经过点(-1,-4),则下列结论中
错误的是( )
A.b2>4ac
B.ax2+bx+c≥-6
C.若点(-2,m),(-5,n)
在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=-4的两根
为-5和-1知2-练4 (2016·陕西)已知抛物线y=-x2-2x+3与x轴交于
A,B两点,将这条抛物线的顶点记为C,连接
AC,BC,则tan∠CAB的值为( )
A. B. C. D.2知2-练 1.二次函数y=ax2+bx+c的图象与x轴的交点有三种情况:
有两个交点、有一个交点、没有交点.与此相对应,一
元二次方程ax2+bx+c=0的根也有三种情况:有两个不相
等的实数根、有两个相等的实数根、没有实数根. 二次
函数y=ax2+bx+c的图象与x轴交点的横坐标就是一元二
次方程ax2+bx+c=0的根.
2.判定抛物线y=ax2+bx+c与x轴交点的个数的方法:当
b2-4ac>0时,有两个交点;当b2-4ac=0时,有一个
交点;当b2-4ac<0时,没有交点.
次方程间的关系1课堂讲解二次函数与一元二次方程间的关系
二次函数与其图象与x轴的交点个数之间的关系2课时流程逐点
导讲练课堂小结作业提升 一元二次方程根的判别式:
式子b2-4ac叫做方程ax2+bx+c=0(a≠0)根的判别式,通
常用希腊字母Δ表示.
(1)当Δ>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根.
(2)当Δ=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根.
(3)当Δ<0时,方程ax2+bx+c=0(a≠0)无实数根.1知识点二次函数的最值 我们已经知道,竖直上抛物体的高度h(m)与
运动时间t(s)的关系可以近似地用公式h=-5t2+ v0t
+h0表示,其中h0 (m/s)是拋出时的高度,v0 (m/s)
是抛出时的速度.一个小球从地面被以40 m/s的速
度竖直向上抛起,小球距离地面的高度h (m) 与
运动时间t(s)的关系如图所示, 那么
(1) h与t的关系式是什么?
(2 )小球经过多少秒后落地?你有几种求解方法?与同伴进行交流.知1-导知1-讲 当二次函数y=ax2+bx+c(a≠0)的y值为0时,
就得到一元二次方程ax2+bx+c=0 .导引:要求抛物线y=3x2-8x+4与x轴的公共点坐标即需
求y=0时对应的x的值;可令y=0,根据3x2-8x+
4=0的根来确定抛物线与x轴的公共点的横坐标.
解:令y=0 , 则3x2-8x+4=0 , 解方程得:x1= , x2=2.
∴抛物线y=3x2-8x+4与x轴的两个公共点的坐标
为 ,(2,0).例1 求抛物线y=3x2-8x+4与x轴的两个公共点的坐标.知1-讲知1-讲 本例将求抛物线与x轴的公共点这个几何
问题转化为求一元二次方程的根的问题来解决,
它充分体现了由形到数的转化思想.1 抛物线y=-3(x-2)(x+5)与x轴的交点坐标为_______.
一元二次方程-3(x-2)(x+5)=0的解为____________.
2 (2016·永州)抛物线y=x2+2x+m-1与x轴有两个不同的
交点,则m的取值范围是( )
A.m<2 B.m>2
C.0<m≤2 D.m<-2知1-练3 (中考·柳州)小兰画了一个函数y=x2+ax+b的图象
如图,则关于x的方程x2+ax+b=0的解是( )
A.无解
B.x=1
C.x=-4
D.x=-1或x=4知1-练2知识点二次函数与其图象与x轴的交点个数之间的关系知2-导 二次函数y=x2+2x, y=x2-2x+1,y=x2-2x+2的图象如图所示.
(1)每个图象与x轴有几个交点?
(2) 一元二次方程x2+2x=0, x2-2x+1=0有几个实数根?用判别
式验证一下.一元二次方程
x2-2x+2=0有实数根吗?
(3)二次函数y=ax2+bx+c的图象
与x轴交点的坐标和一元二
次方程ax2+bx+c=0的根有什么关系?知2-导 二次函数y=ax2+bx+c的图象与x轴的交点有三种情
况:有两个交点、有一个交点、没有交点.
与此相对应,一元二次方程ax2+bx+c=0的根也有
三种情况:有两个不相等的实数根、有两个相等的实
数根、没有实数根.
二次函数y=ax2+bx+c的图象与x轴交点的横坐标就
是一元二次方程ax2+bx+c=0的根.知2-讲 当二次函数y=ax2+bx+c(a≠0)的y值为0时,就得到一元二
次方程ax2+bx+c=0 ,抛物线y=ax2+bx+c与x轴是否有
公共点取决于一元二次方程ax2+bx+c=0的根的情况.
(1)当b2-4ac >0时,方程有两个不相等的实数根,抛物线与x
轴有2个公共点;
(2)当b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴
有1个公共点;
(3)当b2-4ac<0时,方程没有实数根,抛物线与x轴没有公
共点.
反之亦成立.知2-讲拓展:
(1)若一元二次方程ax2+bx+c=0有两个解,且解为
x1,x2,则将多项式ax2+bx+c分解因式得a(x-x1)(x-x2),
所以二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点
(x1,0),(x2,0),函数表达式可表示为y=a(x-x1)·(x-
x2),我们称这种表达式为交点式.
(2)二次函数y=ax2+bx+c的图象与直线y=kx+m的交点坐
标就是方程组 的解,方程组若有两个解,
则两个函数的图象就有两个交点;若有一个解,则两个函
数的图象就只有一个交点;若没有解,则没有交点.知2-讲(3)如果二次函数y=ax2+bx+c的图象与x轴有两个公共点
A(m,0),B(n,0),令m= ,n= ,其中
Δ=b2-4ac.此时A,B两点间的距离
AB=
我们把AB= 叫做抛物线y=ax2+bx+c在x轴上的截距.知2-讲例2 〈荆门改编〉若抛物线y=x2+bx+c与x轴只有一个公
共点,且过点A(m,n),B(m+6,n),则n=_____.导引:∵抛物线y=x2+bx+c与x轴只有一个公共点,∴当x
=- 时,y=0,且b2-4c=0,即b2=4c.又∵抛物
线过点A(m,n),B(m+6,n),∴点A,B关于直线x
=- 对称.
将A点坐标代入抛物线对应的函数表达式,得n=
+c=- b2+c+9,∵b2=4c,
∴n=- ×4c+c+9=9.9知2-讲(1)根据二次函数的图象与x轴的公共点情况可以判断
一元二次方程的根的情况;反之,根据一元二次方
程的根的情况,可以判断二次函数的图象与x轴的
公共点的情况;
(2)拓展:一元二次方程的根的情况由根的判别式定,
二次函数的图象与x轴两公共点间的距离为 ,并
且两公共点关于直线x=- 对称.1 下列抛物线中,与x轴有两个交点的是( )
A.y=3x2-5x+3 B.y=4x2-12x+9
C.y=x2-2x+3 D.y=2x2+3x-4
2 (2016·滨州)抛物线y=2x2-2 x+1与坐标轴的交
点个数是( )
A.0 B.1 C.2 D.3知2-练3 (2015·烟台)如图,已知顶点为(-3,-6)的抛物线
y=ax2+bx+c经过点(-1,-4),则下列结论中
错误的是( )
A.b2>4ac
B.ax2+bx+c≥-6
C.若点(-2,m),(-5,n)
在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=-4的两根
为-5和-1知2-练4 (2016·陕西)已知抛物线y=-x2-2x+3与x轴交于
A,B两点,将这条抛物线的顶点记为C,连接
AC,BC,则tan∠CAB的值为( )
A. B. C. D.2知2-练 1.二次函数y=ax2+bx+c的图象与x轴的交点有三种情况:
有两个交点、有一个交点、没有交点.与此相对应,一
元二次方程ax2+bx+c=0的根也有三种情况:有两个不相
等的实数根、有两个相等的实数根、没有实数根. 二次
函数y=ax2+bx+c的图象与x轴交点的横坐标就是一元二
次方程ax2+bx+c=0的根.
2.判定抛物线y=ax2+bx+c与x轴交点的个数的方法:当
b2-4ac>0时,有两个交点;当b2-4ac=0时,有一个
交点;当b2-4ac<0时,没有交点.
